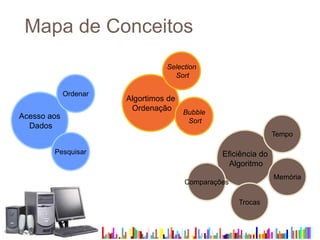
O documento discute algoritmos de ordenação como Selection Sort e Bubble Sort. Explica como ordenar dados ajuda a pesquisar de forma mais eficiente, reduzindo o tempo e recursos necessários. Também descreve os passos dos algoritmos Selection Sort e Bubble Sort e como eles ordenam vetores de dados.

1. Algoritmos de Ordenação
(Intro.)
Selection Sort, Bubble Sort

2. “Imaginem que...”
 Querem telefonar a um amigo a partir do
vosso telemóvel. Como devem proceder?
1. abrir a lista de contactos do telemóvel
2. pesquisar o nome do amigo
3. efectuar a chamada
 Mas e se...
1. a lista de contactos fosse a lista telefónica
nacional?
2. a lista telefónica nacional não estivesse
ordenada?
“... pesquisar toda a lista até encontrar o vosso
amigo!”

3. Pesquisar Vs Ordenar
 O que é pesquisar?
 é encontrar os elementos que satisfazem um
determinado critério (ex: o aluno mais alto)
 O que é ordenar?
 é colocar os elementos em sequência de acordo
com um determinado critério (ex: altura dos
alunos)
 Então quando é que ordenar ajuda a
pesquisar?
 Quando o critério (ou chave) é o mesmo!

4. Vantagens da Ordenação
 Pesquisa mais eficiente
 obtenho o resultado em menos tempo
 obtenho o resultado com menos recursos
 Informação organizada
 posso apresentar a informação ordenada
 posso comparar os elementos mais facilmente
“... o acesso aos dados melhora globalmente!”

5. 1. Seleccionar a menor carta
“Vamos ordenar...”
2. Trocar pela primeira carta
3. Seleccionar a menor carta
4. Trocar pela primeira carta
5. Seleccionar a menor carta
6. Trocar pela primeira carta
7. Seleccionar a menor carta
8. Trocar pela primeira carta
?
Algoritmo de Ordenação

6. Algoritmo de Ordenação
 Em ciências da computação, é um algoritmo
que ordena os elementos de uma sequência
de acordo com um critério...
 Ordenação por Selecção (Selection Sort)
 Mais intuitivo
 Eficiente para um pequeno número de elementos
 A técnica principal é a selecção
 Evolui para uma ordenação parcial

7. Ordenação por Troca (Bubble Sort)
 O Bubble Sort ou ordenação “por bolha”, também é
um algoritmo de ordenação...
 Muito Simples
 A técnica principal é a troca
 Evolui para uma ordenação total
 Eficiente para um pequeno número de elementos
 A ideia é percorrer o vector de elementos e a cada
passagem fazer flutuar para o topo os menores
elementos “... tal como as bolhas de ar num
aquário!”

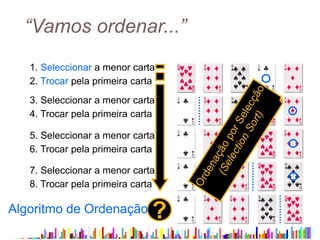
8.  Tendo por base o algoritmo de Ordenação por
Troca (Bubble Sort), ordene o vector V=[10, 6, 8, 2,
5]
“Vamos ordenar...”
para i = n até 1 (-1)
{
para k = 1 até i - 1
{
se v[k] > v[k+1]
{
aux = v[k];
v[k] = v[k+1];
v[k + 1] = aux;
}
}
}
V1 10 6 8 2 5 i k k+1 C T
V2 6 10 8 2 5 5 1 2 1 1
V3 6 8 10 2 5 5 2 3 1 1
V4 6 8 2 10 5 5 3 4 1 1
V5 6 8 2 5 10 5 4 5 1 1
V6 6 8 2 5 10 4 1 2 1 0
V7 6 2 8 5 10 4 2 3 1 1
V8 6 2 5 8 10 4 3 4 1 1
V9 2 6 5 8 10 3 1 2 1 1
V10 2 5 6 8 10 3 2 3 1 1
... ... ... ... ... ... ... ... ... 9 8

9. Qual o Melhor Algoritmo?
Selection
Sort V1 10 6 8 2 5 C T
V2 6 10 8 2 5 1 1
V3 6 8 10 2 5 1 1
V4 6 8 2 10 5 1 1
V5 6 8 2 5 10 1 1
V6 6 8 2 5 10 1 0
V7 6 2 8 5 10 1 1
V8 6 2 5 8 10 1 1
V9 2 6 5 8 10 1 1
V10 2 5 6 8 10 1 1
... ... ... ... ... ... 9 8
Bubble Sort
V1 10 6 8 2 5 C T
V2 2 6 8 10 5 4 1
V3 2 5 8 10 6 3 1
V4 2 5 6 10 8 2 1
V5 2 5 6 8 10 1 1
... ... ... ... ... ... 10 4
C – Comparações
T – Trocas

10. Qual o Melhor Algoritmo?
 Eficiência?
 nº comparações, nº trocas, memória auxiliar,
 tempo processamento, estabilidade
 Complexidade da implementação?
 simples, avançada  memória, tempo
 Técnica de ordenação (comparações, trocas)?
 selecção, troca, ...  nºcomparações, nºtrocas
 Método de comparação (comparações, tempo)?
 numérica, lexicográfica  comparações, tempo
 Evolução da ordenação?
 parcial, total
“... não há algoritmos bons ou maus,
há algoritmos mais ou menos adequados!”

11. Outros Algoritmos
 Simples
 Selection sort
 Insertion sort
 Bubble sort
 Shell sort
 Counting sort
 Avançados
 Quick sort
 Merge sort
 Heap sort
 Radix sort
 Gnome sort
 Bogo sort

12. Algortimos de
Ordenação
Mapa de Conceitos
Acesso aos
Dados
Pesquisar
Ordenar
Eficiência do
Algoritmo
Bubble
Sort
Selection
Sort
Memória
Trocas
Tempo
Comparações