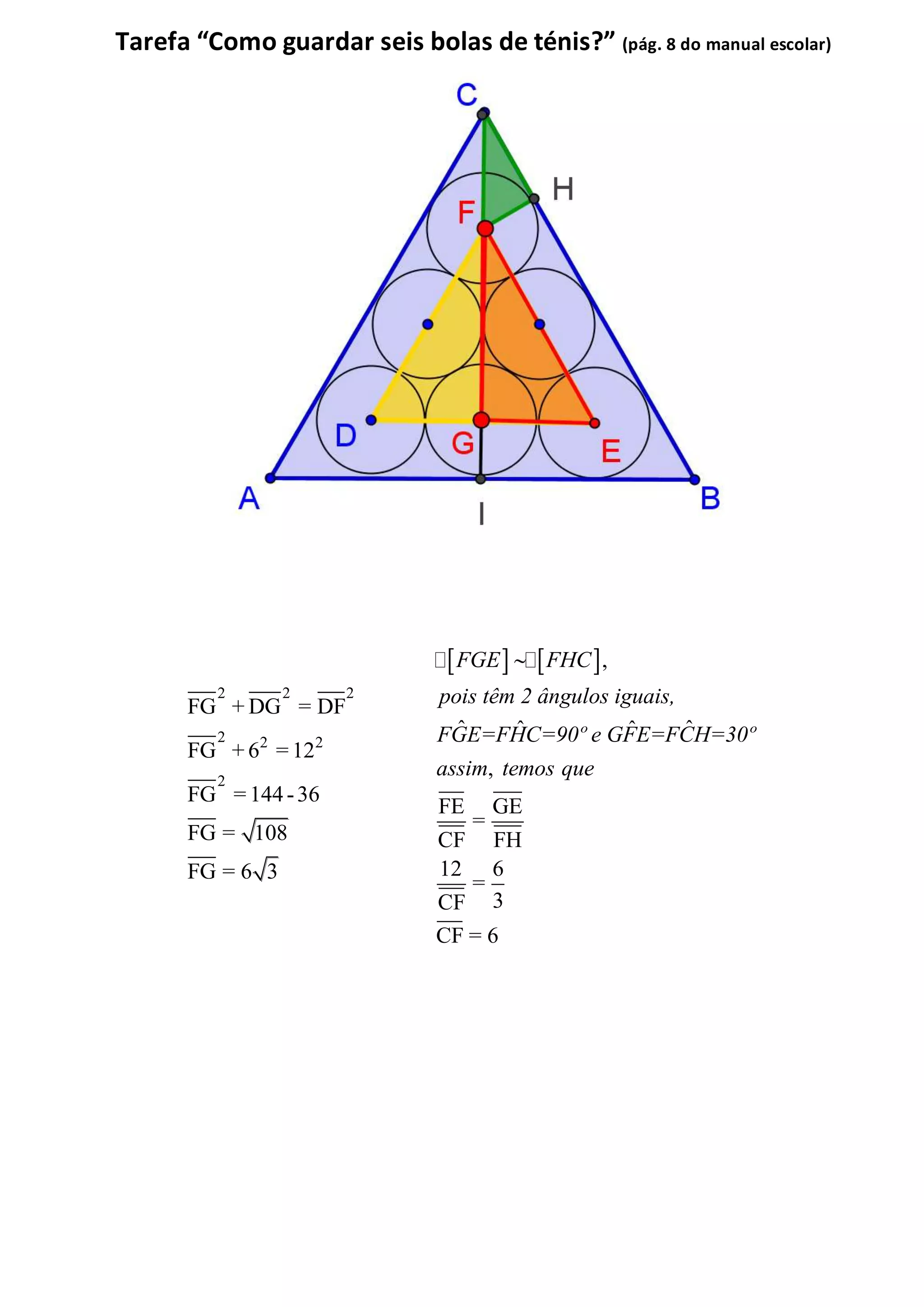
Este documento apresenta cálculos matemáticos para determinar a embalagem mais eficaz para guardar seis bolas de ténis. São calculados os volumes e áreas de três caixas possíveis e comparadas suas capacidades em relação ao volume das bolas. A caixa C, um cilindro, é a mais eficaz por ocupar a menor fração do seu volume com as bolas.

1. Tarefa “Como guardar seis bolas de ténis?” (pág. 8 do manual escolar)
2 2 2
FG +DG = DF
2 2 2
FG + 6 = 12
2
FG = 144 - 36
FG = 108
FG = 6 3
   ,
FGE FHC
pois têm 2 ângulos iguais,
FGE=FHC=90º e GFE=FCH=30º
assim temos que
ˆ ˆ ˆ ˆ
,
FE GE
=
CF FH
12 6
=
CF 3
CF = 6


2. CI = CF FG GI
CI = 6 6 3 3
CI = 9 6 3
 
 

   
Como FGE ∼ FHC , temos
CI CA
 

 

 
=
FG FD
9 6 3 CA
=

6 3 12
12 9 6 3
CA =
6 3
2 9 6 3
CA =
3
18 12 3 3
CA =
3

CA = 12 + 6 3
Q2 – Dimensões de cada caixa:
Caixa A – Paralelepípedo, cuja base é de lado 18 cm por 12 cm e altura de 6 cm.
Caixa B – Prisma triangular regular, com base de lado 12+6 3cme altura de 6 cm.
Caixa C – Cilindro cuja base é um círculo de raio 3 cm e altura de 36 cm.
Q3 – Volume de cada caixa:
3
18×12×6=1296
 12+6 3  9+6 3

×6=
2
 
   
3 3
V
V
= 108+72 3+54 3+36×3 ×3=
= 216+126 3 ×3= 648+378 3 cm 1302,7cm
2 3 3
V  3 3 
1017,9
caixa A
caixa B
caixa C


  
cm
6 = 324 cm cm

3. Área total de cada caixa:
     
  
A  18  12  2  12  6  2  18  6  2 
792
cm
 
12 6 3 9 6 3
A
 
     
   
      
 
2
2 2
     
2 2
C
2 3 12 6 3 6
2
108 72 3 54 3 36 3 18 12 6 3
216 126 3 216 108 3 432 234 3 837,3
3 2 2 3 36 18 216 234 73
Total caixa A
Total caixa B
Total caixa
cm cm
A            
 cm
2 5,1 cm
Q4 – Volume das seis bolas caixa:
    3 3 3 4 4
   
        
   
V  r 6  3 6 4  9 6 216
 cm
esferas 3 3 5.1. – Diferença entre o volume da caixa e o volume das seis bolas:
Caixa A:
3 1296 216  617,5cm
Caixa B:
3 648 378 3  216  624,1cm
Caixa C:
3 324  216 108  339,3cm
5.2. – Razão entre e volume das seis bolas e o volume do caixa:
Caixa A:
0,524
216
1296


Caixa B:
0,521
216
648 378 3



Caixa C:
0,67
216

324


5.3. – Fração de volume de caixa ocupada por cada bola:
Caixa A:
216
1296
6
 3 cm
Caixa A:
 217,1
cm
3 648 378 3
6

Caixa A:
 169,6
cm
3 324
6

6. – Qual a embalagem mais eficaz?
Caixa C