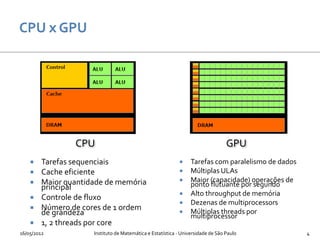
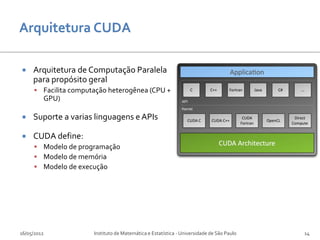
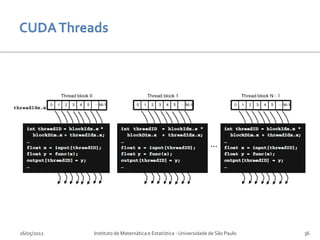
O documento discute o uso de hardware gráfico (GPUs) para computação em finanças. Aborda conceitos como GPU Computing, CUDA e aplicações em precificação de opções e riscos de mercado. Explica as diferenças entre CPUs e GPUs e como o CUDA permite programação paralela em GPUs para aplicações financeiras.












![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes);
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 22](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-22-320.jpg)
![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
// C function vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes);
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 23](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-23-320.jpg)
![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
// ponteiro para host memory {
int *host_array = 0; printf("%d ", host_array[i]);
// aloca espaço em host memory }
host_array = (int*)malloc(num_bytes);
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 24](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-24-320.jpg)
![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes);
// Ponteiro para device memory free(host_array);
int *device_array = 0; cudaFree(device_array);
// Aloca espaço em device memory }
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 25](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-25-320.jpg)
![#include <stdlib.h> // configuracao de bloco e grid
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes);
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 26](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-26-320.jpg)
![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
// extensao __global __ define kernel int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work // lancamento do kernel
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes);
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 27](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-27-320.jpg)
![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void) // transfere resultado da GPU para CPU
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes);
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 28](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-28-320.jpg)
![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements * // inspecao do resultado
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes);
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 29](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-29-320.jpg)
![#include <stdlib.h>
#include <stdio.h> int block_size = 128;
int grid_size = num_elements /
__global__ void kernel(int *array) block_size;
{
//do work
} kernel<<<grid_size,block_size>>>(de
vice_array);
int main(void)
{ cudaMemcpy(host_array, device_array,
int num_elements = 256; num_bytes,
cudaMemcpyDeviceToHost);
int num_bytes = num_elements *
sizeof(int); for(int i=0; i < num_elements; ++i)
{
int *host_array = 0; printf("%d ", host_array[i]);
}
host_array = (int*)malloc(num_bytes); // desaloca memoria
free(host_array);
int *device_array = 0; cudaFree(device_array);
}
cudaMalloc((void**)&device_array,
num_bytes);
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 30](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-30-320.jpg)
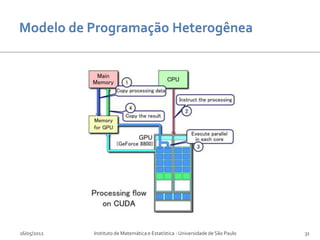

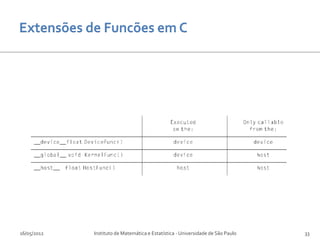

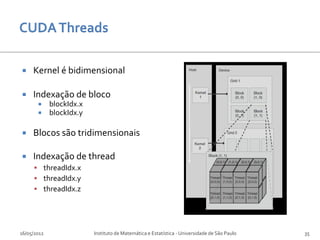








![ Distribuição Normal Padrão Acumulada:
Aproximação como um polinômio de quinta ordem [Hull]:
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 45](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-45-320.jpg)









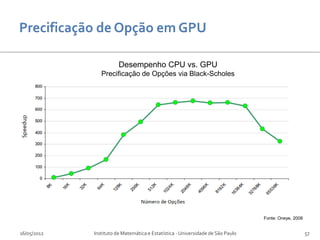
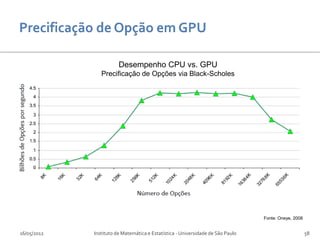






![Desempenho CPU vs. GPU
Método Box-Muller
[Myungho]
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 65](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-65-320.jpg)
![Desempenho CPU vs. GPU
Método Box-Muller
[Myungho]
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 66](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-66-320.jpg)
![Desempenho CPU vs. GPU
Simulação de Monte Carlo
[Myungho]
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 67](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-67-320.jpg)
![Desempenho CPU vs. GPU
Simulação de Monte Carlo
[Myungho]
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 68](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-68-320.jpg)



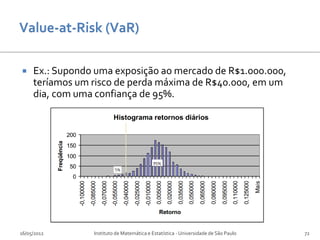


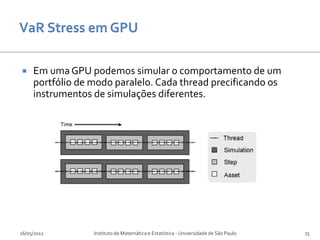

![[Gregoriou]
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 77](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-77-320.jpg)


![I. GPUBrasil (http://gpubrasil.com), Maio 2012.
II. CUDA by example, an introduction to General-Purpose GPU Programming, J. Sanders and E. Kandrot, Addison
Wesley.
III. Programming Massively Parallel Processors: A Hands-on Approach, D. Kirk, W. Hwu, Morgan Kaufman.
IV. NVIDIA CUDA C Best Practices Guide. NVIDIA, Version 3.2, 20/8/2010.
V. NVIDIA CUDA C Programming Guide. NVIDIA, Version 3.2, 11/9/2010.
VI. NVIDIA's Next Generation CUDA Compute Architecture: Fermi. NVIDIA Whitepaper, Version 1.1.
VII. Optimization principles and application performance evaluation of a multithreaded gpu using cuda. Shane
Ryoo, Christopher I. Rodrigues, Sara S. Baghsorkhi, Sam S. Stone, David B. Kirk, and Wen mei W. Hwu. In
PPoPP, pages 73-82. ACM, 2008.
VIII. [Gregoriou] The VaR Implementation Handbook. Greg N. Gregoriou.
IX. [Hull] Options, Futures, and Other Derivatives. John C. Hull.
X. [Myungho] Parallel Implementation of a Financial Application on a GPU. Myungho Lee, Jin-hong Jeon, Jongwoo
Bae, Hyuk-Soo Jang.
XI. [Solomon] Option Pricing on GPU. Steven Solomon, Ruppa K. Thulasiram and Parimala Thulasiraman.
16/05/2012 Instituto de Matemática e Estatística - Universidade de São Paulo 80](https://image.slidesharecdn.com/computacaoemfinanasemhardwaregrafico-120808193415-phpapp01/85/Computacao-em-Financas-em-Hardware-Grafico-80-320.jpg)
