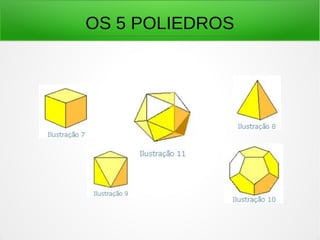
Euclides nasceu na Síria em 325 a.C. e se tornou um importante professor de matemática na Academia de Alexandria no Egito. Sua obra mais famosa foi "Os Elementos", um tratado lógico de geometria em 13 livros que se tornou o texto padrão por mais de 2000 anos.