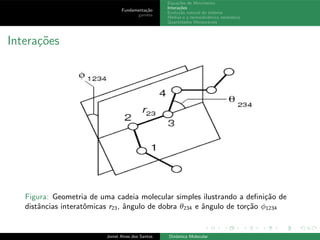
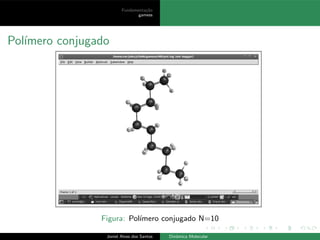
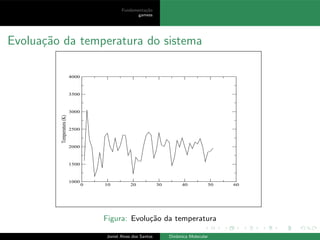
O documento discute os fundamentos da dinâmica molecular, incluindo equações de movimento, interações, evolução do sistema no espaço de fases, médias termodinâmicas e quantidades mensuráveis. A dinâmica molecular simula a evolução natural de sistemas através da integração numérica das equações de movimento de partículas sob forças intermoleculares.