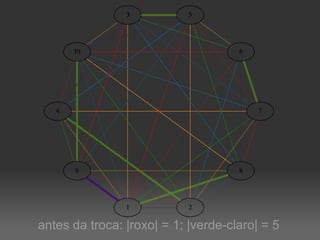
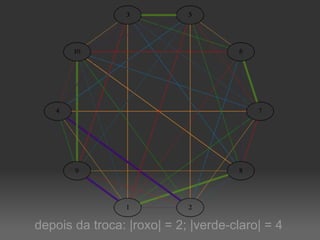
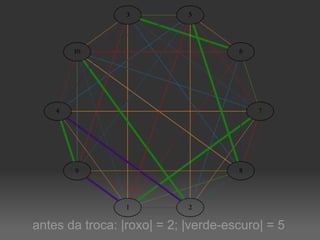
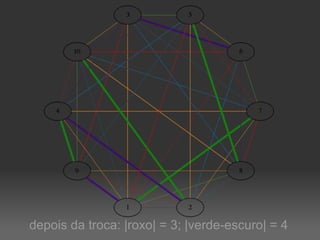
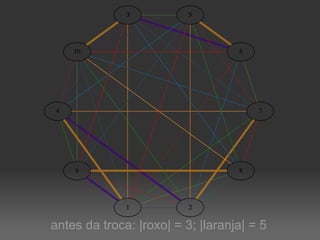
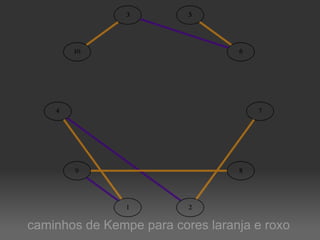
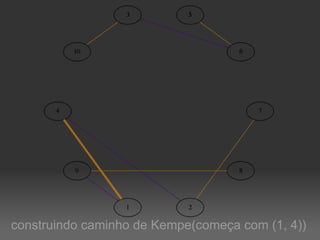
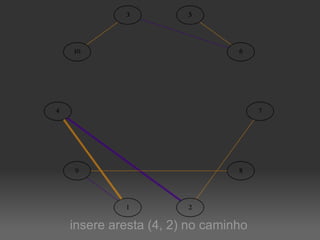
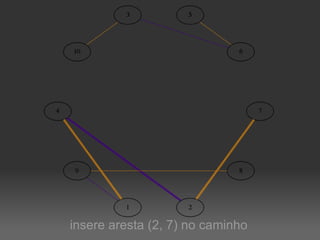
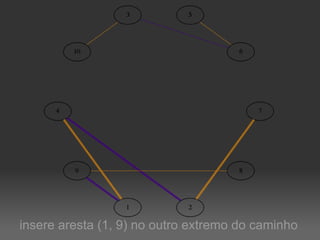
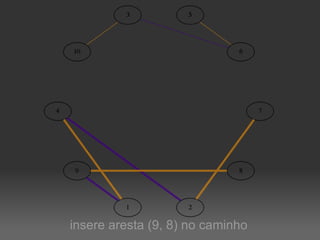
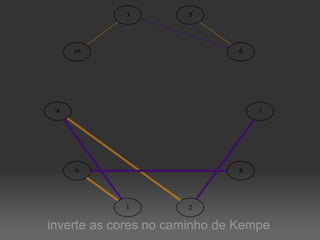
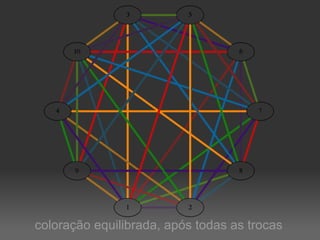
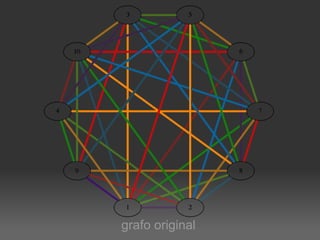
O documento descreve um algoritmo para equilibrar uma coloração de arestas de um grafo, de modo que cada cor seja utilizada aproximadamente da mesma quantidade de vezes. Ele define equilíbrio como usar cada cor entre o piso e o teto da divisão do número de arestas pelo número de cores. O algoritmo implementa caminhos de Kempe para trocar cores entre matchings adjacentes até alcançar uma coloração equilibrada.


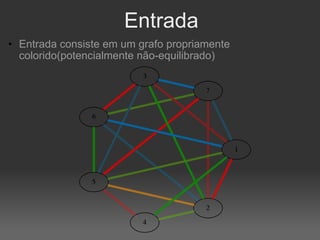
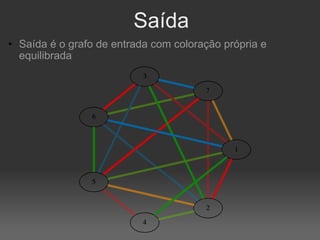

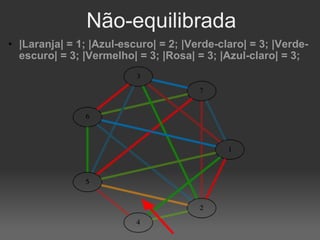
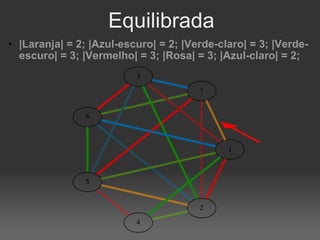

![|V| = 10; |E|=40; k=10; limites=[4, 4]](https://image.slidesharecdn.com/4639023/85/Coloracao-Equilibrada-de-Arestas-9-320.jpg)