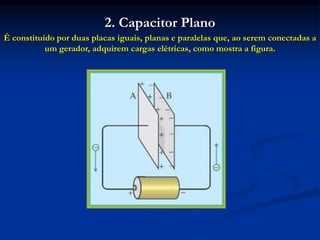
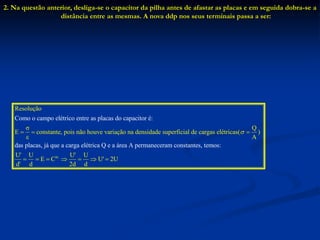
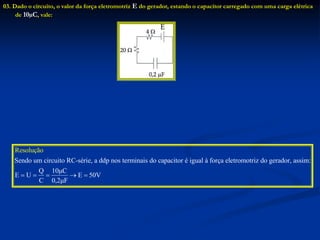
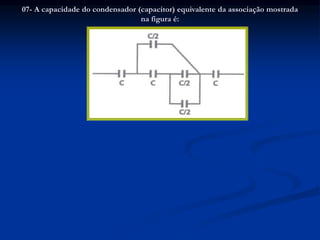
O documento aborda os capacitores, descrevendo sua função como elementos elétricos que armazenam carga elétrica e energia potencial elétrica. Detalha o funcionamento de capacitores planos, sua capacitância, energia armazenada, e as diferentes associações (série e paralelo) de capacitores em circuitos. Exemplos e exercícios resolvidos são fornecidos para ilustrar os conceitos discutidos.

1. Capacitores
1. Capacitores ou Condensadores
 Capacitores ou condensadores são elementos
elétricos capazes de armazenar carga elétrica e,
conseqüentemente, energia potencial elétrica.
 Podem ser esféricos, cilíndricos ou planos,
constituindo-se de dois condutores denominados
armaduras que, ao serem eletrizados, armazenam
cargas elétricas de mesmo valor absoluto, porém
de sinais contrários.

2. 2. Capacitor Plano
É constituído por duas placas iguais, planas e paralelas que, ao serem conectadas a
um gerador, adquirem cargas elétricas, como mostra a figura.

3.  O símbolo do capacitor é constituído por duas barras iguais e planas que representam as
armaduras do capacitor plano.
 Qualquer que seja o tipo de capacitor, sua representação será a mesma do capacitor
plano.
 Quando as placas das armaduras estão eletricamente neutras, dizemos que o capacitor
está descarregado.
 Ao conectarmos o capacitor a um gerador, ocorre um fluxo ordenado de elétrons nos fios
de conexão, pois inicialmente há uma diferença de potencial entre a armadura e o
terminal do gerador ao qual está ligada.
 Na figura do slide anterior, A armadura A tem, inicialmente, potencial elétrico nulo e
está conectada ao terminal positivo da pilha; logo, os elétrons migram da armadura para
a pilha, já a armadura B, que também tem potencial elétrico nulo, está conectada ao
terminal negativo da pilha, e assim elétrons migram do terminal da pilha para a
armadura B.
 Acontece que, enquanto a armadura A está perdendo elétrons, ela está se eletrizando
positivamente e seu potencial elétrico está aumentando; o mesmo ocorre na armadura B,
só que ao contrário, ou seja, B está ganhando elétrons, eletrizando-se negativamente, e
seu potencial elétrico está diminuindo.
 Esse processo cessa ao equilibrarem-se os potenciais elétricos das armaduras com os
potenciais elétricos dos terminais do gerador, ou seja, quando a diferença de potencial
elétrico (ddp) entre as armaduras do capacitor for igual à ddp nos terminais do gerador,
e nesse caso dizemos que o capacitor está carregado com carga elétrica máxima.
 Num circuito, só há corrente elétrica no ramo que contém o capacitor enquanto este
estiver em carga ou em descarga.

4. 3. Capacidade ou Capacitância de um Capacitor
A carga elétrica armazenada em um
capacitor é diretamente proporcional à
diferença de potencial elétrico ao qual foi
submetido.
Assim sendo, definimos capacidade
eletrostática C de um capacitor como a
razão entre o valor absoluto da carga
elétrica Q e a ddp U(ou V) nos seus
terminais.
Q = C.U ou Q=C.V
Essa carga elétrica corresponde à carga de
sua armadura positiva.
Q
C
V

A capacidade eletrostática de um capacitor depende da forma e dimensões de suas
armaduras e do dielétrico (material isolante) entre as mesmas.
A unidade de capacidade eletrostática, no SI, é o farad (F).
1 F = 1 Coulomb/Volt.

5. 4. Energia Armazenada
 O gráfico abaixo representa a carga elétrica Q de um capacitor em
função da ddp U nos seus terminais.
 Q e U são grandezas diretamente proporcionais, o gráfico é uma
função linear, pois a capacidade eletrostática C é constante.
Considerando que o capacitor tenha adquirido a carga Q quando submetido à ddp U do gráfico, a
energia elétrica Welétrica armazenada no capacitor corresponde à área do triângulo hachurado.
e como Q = C.U, então

6. Exercícios Resolvidos
1. Carrega-se um capacitor de capacidade eletrostática 5 µF com carga elétrica
de 20 µC.
Calcule a energia potencial elétrica armazenada no capacitor.
-6
-5
el
-6
-
étrica
6
Resolução
Q Q 20μC 20.10 C
C U U 4V
U C 5μF 5.10
Calculando a ddp U nos terminais do capacitor:
Q.U (20.10 C).(4V)
W
F
4.10 J
2 2
  
 
 

 

7. 2. Um capacitor armazena 8.10–6 J de energia quando submetido à ddp U.
Dobrando-se a ddp nos seus terminais, a energia armazenada passa a ser:
2
2 2
-6
elétrica
elétrica elétrica
2
elétrica
CU'
W' U' 2U
2 W' 4W 32.10 J
CU
W U U
2
Resolução
   
     
   
   

8. 5. Capacidade Eletrostática do Capacitor Plano
 O capacitor plano é constituído de duas placas planas, condutoras, paralelas entre as quais é
colocado um material isolante denominado dielétrico.
 Esse material isolante pode ser: vácuo, ar, papel, cortiça, óleo etc.
Lembrando que no caso de o meio entre as placas ser o vácuo, o valor da constante dielétrica é:
0  8,85.10-12 F/m
ár
A
ea
capa
das
cidade e
placas:
letrostática do capacitor plano depende das seguintes grandezas:
distâ
A
permitiv
ncia e
idade
ntre as plac
elétrica do
as:
m
d
eio:ε



Demonstra-se que a capacidade eletrotática, é dada
ε.A
C
o :
d
p r

d
E
i
st
re
a ex
tame
pressão
nte da c
final permite co
onstante dielétr
ncluir que a capacidade eletrost
ica do meio entre as placas;
in
ática de um capacitor plano depende:
diretamente da A área das placas;
ve


 rsamente da distância d entre as placas.

9. Exercícios Resolvidos
1-Um capacitor plano é conectado a uma pilha de força eletromotriz constante, como mostra a figura,
adquirindo carga elétrica Q. Mantendo-o conectado à pilha, afastam-se as placas até que a
distância entre as mesmas seja o triplo da inicial. Ao término do
processo, sua carga elétrica será:
0 0 0
0
0 0 0
0
0
Re :
A ddp nos terminais do capacitor não m
ε.A ε.A
C e C onde d 3d C 3C
d
udou
d
Q Q Q
Q Q
U U Q
C C 3
.
C C 3
solução
    
      

10. 2. Na questão anterior, desliga-se o capacitor da pilha antes de afastar as placas e em seguida dobra-se a
distância entre as mesmas. A nova ddp nos seus terminais passa a ser:
Resolução
σ Q
E constante, pois não houve variação na densidade superficial de cargas elétr
Como o campo elétrico entre as placas do capacitor é:
das placas, já que a carga elétrica Q e a ár
icas( )
ε
e
A

  
te.
a A permaneceram constantes, temos
U' U U' U
E C U' 2U
d' 2d d
:
d
      

11. 6. Associação de Capacitores
Da mesma forma que os resistores, geradores e receptores, os capacitores também podem ser
associados em série, em paralelo ou em associações mistas.
 Associação em série
Dois ou mais capacitores estarão associados em série quando entre eles não houver nó, ficando,
dessa forma, a armadura negativa de um ligada diretamente à armadura positiva do outro.
Ao estabelecermos uma diferença de potencial elétrico nos terminais da associação, haverá
movimentação de elétrons nos fios que unem os capacitores até que estes estejam completamente
carregados.
Ao ser conectada ao terminal positivo da pilha, a armadura do
capacitor C1 fica eletrizada positivamente e induz uma
separação de cargas no fio que o liga ao capacitor C2, atraindo
elétrons para sua outra armadura que fica eletrizada
negativamente e, conseqüentemente, eletrizando a armadura
positiva do capacitor C2, que por sua vez induz uma separação
de cargas no fio que une este ao capacitor C3, e assim por
diante.
Esse fato nos permite concluir que:
– todos os capacitores ficam carregados com a mesma carga elétrica Q;
– a carga elétrica armazenada na associação é igual a Q, pois foi essa quantidade que a
pilha movimentou da armadura positiva do capacitor C1 para a armadura negativa do
capacitor C3.

12. Capacitor equivalente de uma associação em
série
Denominamos Capacitor Equivalente aquele
capacitor que, submetido à mesma ddp U que a
associação, adquire a mesma carga elétrica Q da
associação.
Para a associação em série temos:
por ser uma associação em série, a ddp U nos terminais da associação é igual à soma
das ddps individuais em cada capacitor.

1 2 3
U U U U
  
Para o capacitor equivalente, temos:
1 2 3
S
Q
U e, como U U U U
C
    
Sendo a ddp em cada capacitor:
1 2 3
1 2 3
Q Q Q
U ; U ; U .
C C C
   
S 1 2 3 S 1 2 3
Q Q Q Q 1 1 1 1
= + + = + +
C C C C C C C C

Regra para ser aplicada para dois
capacitores em série de cada vez.
2 1 1 2
S
S 1 2 S 1 2 1 2
C C C .C
1 1 1 1 Produto
C
C C C C C .C C C Soma

      


13.  Associação em paralelo
Dois ou mais capacitores estão associados em paralelo
quando seus terminais estão ligados aos mesmos nós e,
conseqüentemente, sujeitos à mesma diferença de potencial U.
Na figura, os capacitores estão com seus terminais ligados aos
mesmos nós A e B.
Conectando os nós A e B aos terminais da pilha, os capacitores ficam sujeitos à mesma ddp U e, se
suas capacidades eletrostáticas forem diferentes, adquirem cargas elétricas Q1 e Q2 diferentes entre si.
As armaduras ligadas ao nó A cedem elétrons para a pilha e as ligadas ao nó B recebem elétrons da
pilha, de modo que a carga elétrica total movimentada pela pilha, das armaduras positivas para as
negativas, é igual à soma das cargas Q1 e Q2, até atingido o equilíbrio eletrostático.
 Portanto, concluímos que:
– a carga elétrica Q armazenada na associação é igual à soma das cargas elétricas armazenadas em cada
capacitor:
Q=Q1+Q2
– essa carga elétrica é igual à quantidade de carga elétrica movimentada pela pilha das armaduras
positiva para as negativas dos capacitores da associação;
– por ser uma associação em paralelo, a ddp U nos terminais A e B da associação é a mesma para todos
os capacitores.

14. Capacitor equivalente de uma associação em
paralelo
Como Q = Q1 + Q2, então CP · U = C1 · U + C2 · U
a capacidade eletrostática do capacitor equivalente é dada por:
CP= C1 + C2
A carga elétrica em cada
capacitor é:
Q1 = C1 .U e Q2 = C2 .U
No capacitor
equivalente temos:
Q = CP .U
Importante! Note Bem!
Qualquer que seja o tipo de associação, série, paralelo ou mista, a energia elétrica
armazenada na associação é igual à soma das energias elétricas de cada capacitor
individualmente e que é igual à energia elétrica no gerador equivalente.
WASSOCIAÇÃO=W1+W2+W3+...+Wn

15. 7.Circuitos com Capacitores
 Existem circuitos constituídos de geradores, receptores e resistores. A esses circuitos podemos
acrescentar capacitores que poderão estar em série ou em paralelo aos elementos do mesmo.
A. Circuito com Capacitor em Série
Quando o capacitor está carregado, a ddp UXZ nos terminais do capacitor é igual à ddp UXY nos
terminais do gerador, pois, no resistor, não havendo corrente não há ddp (UYZ = 0), ou seja, os
potenciais elétricos de Y e Z são iguais. Nesse caso então UXZ = UXY = E (fem) do gerador pois este se
encontra em circuito aberto.
Circuito RC-série
(resistor-capacitor em série).
Com a chave Ch aberta(figura1) não há corrente.
Ao fechar-se a chave Ch circulará no circuito
uma corrente elétrica (figura 2) que diminui de
intensidade com o decorrer do tempo até o
instante em que se torna nula.
Essa corrente é proveniente dos elétrons que
abandonam a armadura positiva do capacitor,
circulam pelo resistor e pelo gerador e alojam-se
na armadura negativa do capacitor sem
atravessá-lo, devido ao dielétrico (isolante) entre
as placas.

16. B. Circuito com Capacitor em Paralelo
B. Circuito com Capacitor
em Paralelo
AB
eq
E
U =R.i onde i
r R


circuito RC-paralelo
(resistor-capacitor em paralelo).
Com o capacitor já carregado, não há mais passagem de corrente pelo ramo do capacitor.
Pelo fato de o capacitor estar em paralelo com o resistor, ambos estão sujeitos à mesma ddp U, tal que:
Na figura 1, a chave Ch está aberta e, assim,
não há corrente no circuito, nem ddp entre
os terminais A e B do resistor e do capacitor.
Ao fecharmos a chave Ch (figura 2),
estabelece-se uma corrente no circuito e,
conseqüentemente, haverá ddp entre A e B.
Durante um intervalo de tempo muito
curto, há uma corrente decrescente no
ramo do capacitor, enquanto este está
se carregando. Essa corrente não
atravessa o capacitor por causa do
dielétrico (isolante) entre as placas.
AB
A carga elétrica,Q, armazenada no capacitor é dada por:
Q C.U


17. Exercícios Resolvidos
 01. Dois capacitores de capacidades eletrostáticas C1 = 2µF e C2 = 6µF estão associados em série e ligados a uma
fonte que fornece uma ddp constante de 20 V. Determinar:
a) a capacidade eletrostática do capacitor equivalente;
b) a carga elétrica de cada capacitor;
c) a ddp nas armaduras de cada capacitor.
1 2
S
1 2
a) Calculo da capacidade equivalente:
C .C 2.6
C 1,5μF
C C 2 6
  
 
1 2
S
b) A carga do capacitor equivalente é igual à carga
de cada capacitor: Q = Q = Q
Q C .U Q 1,5μF.20V Q 30μC
    
1 1
1
2 1
2
Q Q 30μC
c) Como U , temos:U U 15V e
C C 2μF
Q 30μC
U U 5V
C 6μF
    
   

18. 02. Dois capacitores de capacidades eletrostáticas C1 = 2µF e C2 = 6µF estão associados em paralelo e ligados a uma fonte que fornece
uma ddp constante de 30 V. Determinar:
a) a capacidade eletrostática da associação;
b) a carga elétrica de cada capacitor;
c) a energia elétrica armazenada na associação.
p 1 2
a) Calculando a capacidade equivalente:
C C +C
Resoluçã
2μF 6μF 8μF
o
   
1 1 1
2 2 2
b) Sendo Q C·U e como U é a mesma para todos, temos:
Q C .U 2μF.30V Q 60μC
Q C .U 6μF.30V Q 180μC

   
   
1
1 1
2
2 1
Q.U
c) Sendo a energia elétrica dada por: W
2
Q .U 60μC.30V
W W 900μJ
2 2
Q .U 180μC.30V
W W 2700μJ
2 2

   
   

19. 03. Dado o circuito, o valor da força eletromotriz E do gerador, estando o capacitor carregado com uma carga elétrica
de 10µC, vale:
Sendo um circuito RC-série, a ddp nos terminais do capacitor é igual à força eletromotriz do gerador, assim:
Q 10μC
E U E 50V
C 0,2
R
μ
esoluçã
F
o
    

20. 04. A carga e a energia elétrica armazenada no capacitor do circuito abaixo valem, respectivamente:
eq
120V
Trata-se de um circuito RC-paralelo e, para calcular a ddp U nos terminais do resistor,
dev
Resolução
Sendo
emos prime
i i i 5A
r
iro calcular a corrente no circuito.
A ddp U nos terminai
4 20
s
+R
ε
    
  
ELÉTRICA ELÉTRI
do capacitor e nos terminais do resistor são iguais:
A carga elétrica no capacitor,é:
A energia armazenada pelo capacitor é
U=R.i U=20V.5A U=100V
Q=C.U Q 0,2μF.100V Q 20μC
Q.U
W
dada po
W
r:
2
 
   
  CA ELÉTRICA
20μC.100V
W 1000μJ
2
  

21. Questões da Apostila
Questões de Treinamento(Página 148)
01-As armaduras de um capacitor plano a vácuo apresentam área A=0,10m2 e estão
situadas a uma distância d=2,0cm. Esse capacitor é carregado sob ddp U=1000V.
Determine: (Considerando 09.10-12 F/m)
a) A capacitância do capacitor;
b) A carga elétrica do capacitor.

22. Resolução
-12 2
-11
0
-2
-11 -8
QT01
F
8,8.10 .0,10m
ε .A m
a) C 4,4.10 F
d 2,0.10 m
b) Q C.U 4,4.10 F.1000V 4,4.10 C
  
  

23. 02- Um capacitor é constituído por duas placas planas e paralelas, cuja capacitância
pode ser modificada variando a distância entre as placas.
Com capacitância de 5.10-10F, foi carregado o capacitor com 100V e, a seguir,
desligado do gerador.
Em seguida afastam-se as placas até a capacitância cair a 10-10F. Calcule a nova ddp
entre as placas.

24. Resolução
-10
-10
QT02
Q Q U' C 5.10 F
C e C' U' .100V 500V
U U' U C' 10 F
      

25. 03-Um capacitor de capacitância C=2.10-6F é ligado a uma pilha de fem 3V e
resistência interna r=0,1. Calcule a carga e a energia potencial elétrica do
capacitor.

26. Resolução
-6 -6
2 -6 2
-6
QT03
O capacitor estará totalmente carregado quando a ddp entre suas
armaduras for igual a fem do gerador.
Q C.U 2.10 F.3V 6.10 C 6μC
C.U 2.10 F.(3V)
E 9.10 J 9μJ
2 2
   
   

27. 04-Três capacitores são associados conforme a figura.
Fornecendo-se à associação a carga elétrica de 12C, determine:
a) A carga elétrica e a ddp em cada capacitor;
b) A ddp da associação;
c) A capacitância do capacitor equivalente;
d) A energia potencial elétrica da associação.

28. Resolução
1 2 3
1 2 3
AB 1 2 3
eq
eq 1 2 3 eq
eq
ASSOC
QT04
a) A carga elétrica é a mesma em todos os capacitores(12μC).
Q 12μC Q 12μC Q 12μC
V 4V V 3V V 2V
C 3μF C 4μF C 6μF
b) V V V V 9V
1 1 1 1 1 1 1 1 4
c) C μF
C C C C C 3μF 4μF 6μF 3
C .
d) E
        
   
        

2
2
AB
4
μF.(4V)
(V ) 3 54μJ
2 2
 

29. 05-Três capacitores são associados conforme a figura.
Aplicando-se entre A e B a ddp de 100V, determine:
a) A ddp e carga elétrica em cada capacitor;
b) A carga elétrica da associação;
c) A capacitância do capacitor equivalente;
d) A energia potencial elétrica da associação.

30. Resolução
ASSOC 1 2 3
1 2 3 AB
1 1 1 2 2 2
3 3 3
QT05
Determinação da capacitância do capacitor equivalente
C C C C 2μF 5μF 10μF 17μF
A ddp é a mesma em todos os capacitores V V V V 10V
Q C .V 2μF.10V 20μC Q C .V 5μF.10V 50μC
Q C .V
      
   
       
 ASSOC 1 2 3
2 2
eq AB
ASSOC
10μF.10V 100μC Q Q Q Q 170μC
C .(V ) 17μF.(10V)
E 850μJ
2 2
      
  

31. 06-Para o esquema dado, determine:
a) A carga elétrica total armazenada pela associação;
b) A energia potencial elétrica armazenada pela associação.

32. Resolução
ASSOC ASSOC
2
eq AB
ASSOC
QT06
Determinação da capacitância do capacitor equivalente
1μF em série com 1μF 0,5μF
2μF em série com 2μF 1μF
0,5μF em paralelo com 1μF 1,5μF
a) Q C .U 1,5μF.100V 150μC
C .(V ) 1,5μF
b) E
2



  
 
2
3
.(100V)
7,5.10 J
2



33. 07- A capacidade do condensador (capacitor) equivalente da associação mostrada
na figura é:

34. Resolução
QT07 (OpçãoB)
C C
i) em paralelo com equivalente igual a C
2 2
C
ii) C em série com C equivalente igual a
2
C C
iii) em paralelo com equivalente igual a C
2 2
iv) Três iguais a C em série equivalente igual a




C
3

35. OBJETIVAS
01- O gerador do circuito a seguir é ideal.
(A) 2V (B) 4V (C) 8V (D) 16V (E) 32V
A ddp nos terminais do capacitor de 3F é de :

36. Resolução
QO01 (OpçãoD)
A ddp nos terminais da associação é igual a ddp nos terminais do resistor de 8 .
A intensidade de corrente elétrca que atravessa o resistor de 8Ω é dada por :I
30V
Seu valor é: I
2 8
r R





 
8Ω
ASSOC ASSOC ASSOC
3A
A ddp nos terminais de R 8 é: U R.I 8 .3A 24V
A capacitância equivalente de (4μF em paralelo com 2μF) e em série com 3μF é igual a 20μF.
A carga elétrica da associação é: Q C xU 48μ


     
 
3
3
3
C.
A carga elétrica no capacitor é também de 48μC.
Q 48μC
A ddp nos terminais do capacitor de 3μF é: U 16V.
C 3μF
  

37. 02- No circuito mostrado na figura a seguir, a força eletromotriz da bateria é
  10V e sua resistência interna é r  1,0.
Sabendo que R  4,0 e C  2,0F, e que o capacitor já se encontra completamente carregado, considere
as seguintes afirmações:
I. A indicação do amperímetro é 0A;
II. A carga armazenado no capacitor é de 16F;
III. A tensão entre os pontos a e b é 2,0V;
IV. A intensidade de corrente na resistência R é de 2,5A.
Das afirmativas mencionadas, é (são) correta(s):
(A) Apenas I (B) I E II (C) I e IV (D) II e III (E) II e V

38. Resolução
ab ab
QO02(OpçaõB)
Se o capacitor está completamente carregado, não circula corrente elétrica no ramo onde
ele se encontra.(Afirmação I verdadeira).
A ddp nos terminais do capacitor é dada por: Q C.U e U é

ab ab
ab
calculado pelo produto
ε
R.I e I é dado por ;Calculo dos valores citados :
r R
ε 10V
I 2,0A.(Afirmação IV falsa).
r R 1,0 4,0
U R.I 4,0 .2,0A U 8,0V.(Afirmação III falsa).
Q C.U 2,0μF.8,0V Q 16μC.(Afi

  
   
    
    rmação II verdadeira).

39. 03- Na figura cada capacitor tem capacitância de C11F.
Entre os pontos A e B existe uma ddp de 100V.
Qual é a carga elétrica total armazenada no circuito?
(A) 3,0.10-5 C (B) 4,0.10-5 C (C) 5,0.10-5 C (D) 6,0.10-5 C (E) 7,0.10-5 C

40. Resolução
A
A
A
B B
B
C
C
C
4C/11
C/3 4C/3
C
C
AB AB AB
QO03(OpçaõB)
4
Q C .U .11μF.10V Q 40μC.
11
   

41. 04- No circuito, a lâmpada L apresenta inscrição nominal (3W-6V), o gerador é
considerado ideal e o capacitor não apresenta carga elétrica. No momento que a
chave Ch é fechada, a lâmpada acende e o amperímetro ideal A1 acusa uma
intensidade de corrente igual a 0,10A. Instantes depois, a lâmpada apaga, esse
mesmo amperímetro marcas zero e o amperímetro A2, também ideal, indica:
(A) 0,10A (B) 0,20A (C) 0,30A (D) 0,40A (E) 0,50A

42. Resolução
2 2
POT
QO04(OpçaõB)
U (6V)
O valor da resisitência da lâmpada é dado por: R 12 .
P 3W
   
2μF
A1
A2
3W-6V
6
CH
6Ω 6Ω 6Ω
2
6Ω 6Ω
Note que, U (R ).(I ) ε 1,2V.
Com o capacitor totalmente carregado toda corrente elétrica passará pelo
resistor de 6 ,cuja intensidade é dada pelo amperímetroA .
ε (R ).(I' ) 1,2V (6Ω).I' I' 0,20
  

     A.
L
R 12
 

43. 05- No circuito a seguir, estando o capacitor com plena carga, levamos a chave k da posição
I para II. A quantidade de energia térmica liberada pelo resistor de 5 após essa operação
é:
(A) 1 J (B) 3 J (C) 6 J (D) 12 J (E) 15 J

44. Resolução
2 -3 2
QO05(OpçaõC)
A ddp nos terminais do capacitor é de 20V.
C.U 30.10 F.(20V)
A energia armazenada por ele é: E 6J.
2 2
Essa energia será dissipada por Efeito Joule no resistor de 5 .
  


45. Questões Discursivas
01- Um raio entre uma nuvem e o solo ocorre devido ao acúmulo de carga elétrica na base
da nuvem, induzindo uma carga de sinal contrário na região do solo abaixo da nuvem. A
base da nuvem está a uma altura de 2 km e sua área é de 200 km2.
Considere uma área idêntica no solo abaixo da nuvem. A descarga elétrica de um único raio
ocorre em 10-3s e apresenta uma corrente de 50 kA.
Considerando 09.10-12 F/m, responda:
a) Qual a carga elétrica armazenada na base da nuvem no instante anterior ao raio?
b) Qual é a capacitância do sistema nuvem-solo nesse instante?
c) Qual a ddp entre a nuvem e o solo, imediatamente antes do raio?

46. Resolução
3 -3
-12 3 2
7
0
3
7
-7
QD01
a) ΔQ IxΔt 50.10 Ax10 s Q 50C.
F
9.10 .200(10 m)
ε A m
b) C 9.10 F.
d 2.10 m
Q 50C
c) Q CU U 5,0.10 V.
C 9.10 F

    
  
    

47. 02- Para tirar fotos da festa de aniversario da filha, o pai precisou usar o flash da maquina
fotográfica. Este dispositivo utiliza duas pilhas de 1,5V, ligadas em série, que carregam
completamente um capacitor de 15F. No momento da fotografia, quando o flash é
disparado, o capacitor, completamente carregado, se descarrega sobre sua lâmpada, cuja
resistência elétrica é igual a 6.
Calcule o valor máximo:
a) da energia armazenada no capacitor;
b) da intensidade de corrente elétrica que passa pela lâmpada quando o flash é disparado.

48. Resolução
2
5
QD02
CU
a) E 6,75.10 J.
2
U
b) U R.I I 0,50A.
R

 
   

49. 03- Para a segurança dos clientes, o supermercado utiliza lâmpadas de emergência
e rádios transmissores que trabalham com corrente continua. Para carregar suas
baterias, no entanto, esses dispositivos utilizam corrente alternada. Isso é possível
graças a seus retificadores que possuem, cada um, dois capacitores de 1.400F,
associados em paralelo. Os capacitores, descarregados e ligados a uma rede
elétrica de tensão máxima igual a 170V, estarão com carga plena após um certo
intervalo de tempo t.
Considerando t, determine:
a) a carga elétrica total armazenada;
b) a energia potencial elétrica total armazenada.

50. Resolução
1 2
2 2
P
QD03
a) C C C 2800μF Q CU 2800μF.170V Q 0,48C.
CU 2800μF.(170V)
b) E 40,5J
2 2
       
  

51. Transformador ideal
 A aplicação de uma corrente variável com o tempo em uma das bobinas gera um fluxo
magnético que, por sua vez, induz uma tensão na outra conforme lei de Faraday.
 A bobina que recebe a corrente é denominada bobina ou enrolamento primário. Na
bobina ou enrolamento secundário, está presente a tensão induzida.
 A relação entre a tensão(ddp) e fluxo magnético(em módulo) nos enrolamentos primário
e secundário, são:
 UPNP.(Pt) e USNS.(St)  onde N é o número de espiras.
 Na situação ideal, o fluxo magnético gerado no primário é totalmente dirigido ao
secundário, de forma que P = S = .
 Podemos então dividir as igualdades e chegamos à relação básica do transformador :
Um transformador ideal pode ser esquematizado
conforme a Figura . Duas bobinas compartilham o
mesmo núcleo. O material deste é altamente magnético
(em geral o ferro), de forma que todo o fluxo magnético
gerado é conduzido pelo núcleo.
UP/ US NP/ NS
Na condição ideal também temos a mesma potência
em cada bobina: P = UP .Ip = Us Is.
Combinando com a relação anterior,
Is / Ip = Np / Ns

52. Questão de treinamento
07 página 122
P P P
s2 s2 s2
Total P P S1 S1 S2 S2 S1 S1
N U N 8800V
a) 40
N U N 220V
b) P U .I U I U I 81000 120 .I 220V.150A I 400 .
W V A
   
       