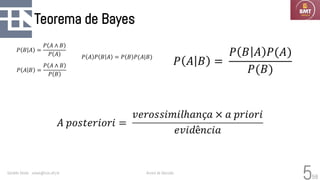
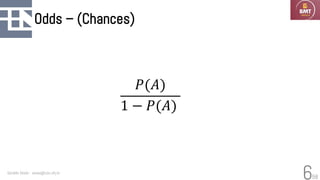
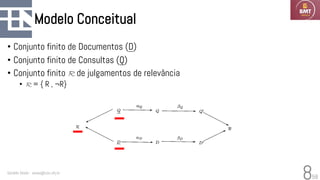
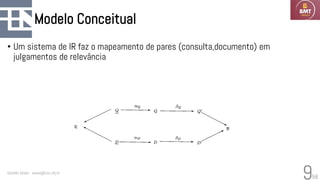
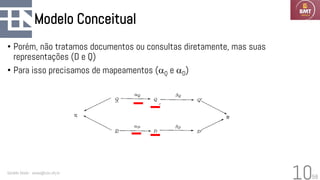
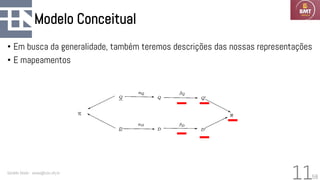
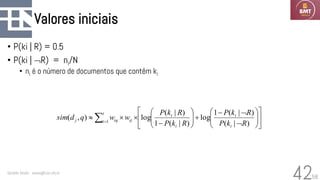
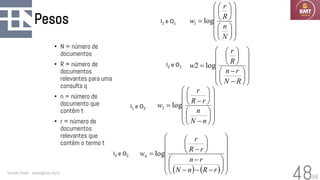
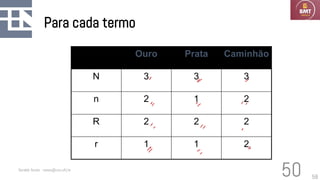
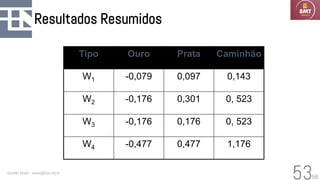
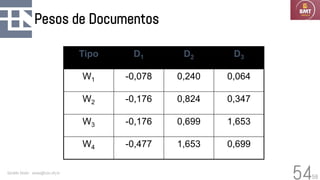
O documento discute modelos probabilísticos para sistemas de recuperação de informação, introduzindo conceitos como probabilidade condicional, teorema de Bayes e independência binária. Ele fornece as bases para estimar a probabilidade de um documento ser relevante para uma consulta usando a distribuição de termos.