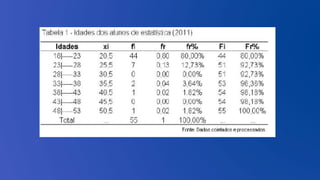
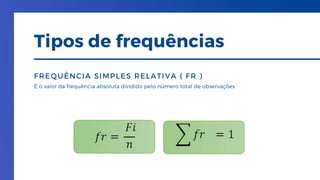
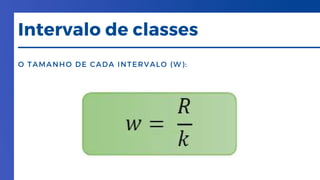
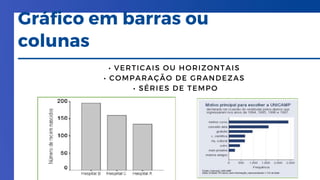
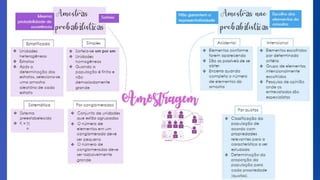
O documento discute a importância da bioestatística na condução e avaliação de pesquisas, abordando a comparação entre grupos e a identificação de variáveis interferentes. Ele detalha os tipos de variáveis, amostragem probabilística e não probabilística, e métodos de análise estatística, como tabelas e gráficos. A importância da didática científica e a flexibilidade do conhecimento científico são também ressaltadas.

1. BIOESTATÍSTICA

2. A condução e avaliação de uma
pesquisa depende,
em boa parte, do conhecimento
sobre Bioestatística
Comparação
entre dois ou mais grupos ou amostras
(grupo tratado / grupo controle)
ESTAR ALERTA A: VARIÁVEIS INTERFERENTES NOS RESULTADOS
¤ VARIAÇÕES MOSTRAIS
¤ DIFERENÇAS ENTRE GRUPOS

3. Os testes estatísticos são utilizados
para:
¤ Comparar amostras
(houve modificação dos grupos
inicialmente semelhantes após o início da
intervenção)
¤ Detectar variáveis interferentes
¤ Analisar se o tratamento depende de
outras variáveis (peso, idade, sexo)

4. A ciência não é um
conhecimento definitivo
sobre a realidade, mas é
um conhecimento
hipotético que pode
ser questionado
e corrigido.
Ensinar
ciências não significa
apenas descrever
fatos, anunciar leis e
apresentar
novas descobertas, mas
Ensinar o método científico
Maneira crítica e racional de buscar
conhecimento

5. Tipos de variáveis
É a característica de interesse que é
medida em cada elemento da
amostra/população;
Variam de elemento para elemento;
Podem ter valores numéricos ou não numéricos.

6. Quantitativas
CONTÁVEL
DISCRETAS
Uso de números inteiros
EX. N° DE FILHOS;
IDADE (1, 2, 10, 24, 56);
PATRIMÔNIO;
CONTÍNUA
MENSURÁVEL;
NÚMEROS DECIMAIS; USUALMENTE
DEVEM SER MEDIDAS ATRAVÉS DE
ALGUM INSTRUMENTO.
EX.; SALÁRIO; ALTURA; IDADE (ANO +
MESES); TEMPERATURA;

7. ORDINAL
HIERARQUIA.
EX. Cargo; Escolaridade; Dor; Nível social;
Idade (criança, adolescente, adulto, idoso);
Qualitativas

8. DICOTÔMICA
SOMENTE DUAS CATEGORIAS.
EX. Masculino e feminino; Sim e não; Aberto
e fechado;
Nominal

9. MAIS DE DUAS
CATEGORIAS.
EX. TIPO SANGUÍNEO;
SIGNOS; RELIGIÃO;
PROFISSÃO;
Uma variável quantitativa pode ser coletada de
forma qualitativa.
Categórica

10. Conceitos
→ População (N)
O conjunto de elementos a serem observados.
→ Amostra (n)
É uma pequena parte selecionada de uma população que se
pretende estudar.
Fazemos amostragem quando:
- O numero de elementos da população é muito grande
- Queremos economizar tempo e dinheiro
- Não é possível acessar todos os elementos da população

11. Amostragem
É preciso definir os critérios que
serão usados para selecionar as
unidades que vão compor a amostra
Antes de obter a amostra
,
Item 1 Item 2 Item 3 Item 4
40
30
20
10
0

12. Amostra
probabilística
Retiradas ao acaso da população
- Sorteio
• Mesma probabilidade de ocorrência
• A população deve ser conhecida
• Cada unidade é identificada por um
nome ou numero
• Pode ser simples ou estratificada
,
Item 1 Item 2 Item 3 Item 4
40
30
20
10
0

13. Aleatória
Simples
• Sorteia-se um por um
• Unidades homogêneas
• Quando a população é
finita e não
demasiadamente grande
• 1 a N.

14. Aleatória
Estratificada
• Unidades heterogêneas
Sexo, idade, escolaridade, nível salarial
• Devem ser identificadas
As unidades similares devem ser reunidas
em subgrupos (estratos)
• Após a determinação dos estratos,
seleciona-se uma amostra aleatória de
cada estrato

15. Amostra semi-
probabilística

16. • RETIRADAS DA POPULAÇÃO POR PROCEDIMENTO
PARCIALMENTE ALEATÓRIO
• SISTEMÁTICA E POR CONGLOMERADOS

17. Sistemática
Ex uma amostra constituída por 1/8 da população, você sorteia
um número que caia entre 1 e 8. Se for sorteado o numero 3, a
terceira unidade da população será selecionada para a amostra.
A partir daí, tome sistematicamente, a terceira unidade de cada
8, em sequência n = {3, (3+8 = x), (x+8) ...}
RETIRADAS DA POPULAÇÃO POR UM SISTEMA
PREESTABELECIDO
K: INTERVALO DE AMOSTRAGEM D: NÚMERO INICIAL

18. CONGLOMER
ADO É UM
CONJUNTO
DE
UNIDADES
QUE ESTÃO
AGRUPADAS
UM ASILO É
UM
CONGLOMER
ADO DE
IDOSOS
O NÚMERO
DE
ELEMENTOS
EM UM
CONGLOMER
ADO DEVE
SER
PEQUENO
O NÚMERO
DE
CONGLOMER
ADOS DEVE
SER
RAZOAVELM
ENTE
GRANDE
POR CONGLOMERADOS

19. POR CONGLOMERADOS
EX. UM DENTISTA QUE LEVANTAR DADOS SOBRE A
NECESSIDADE DE APARELHO ORTODÔNTICO EM CRIANÇAS DE
12 ANOS. ELE PODE SORTEAR TRÊS ESCOLAS DE PRIMEIRO
GRAU (CONGLOMERADO) E EXAMINAR AS CRIANÇAS ALVO
DESSA ESCOLA

20. Amostra não
probabilística
Há uma escolha deliberada dos elementos da
amostra
INTENCIONAL OS RESULTADOS
NÃO SÃO
GENERALIZÁVEIS
NÃO GARANTEM A
REPRESENTATIVIDA
DE DA POPULAÇÃO
ACIDENTAL, INTENCIONAL E POR QUOTAS

21. ENCERRA QUANDO
COMPLETA O
NÚMERO DE
ELEMENTOS DA
AMOSTRA
FORMADA POR
ELEMENTOS
CONFORME FOREM
APARECENDO
ELEMENTOS SÃO OS
POSSÍVEIS DE SE
OBTER
ACIDENTAL
EX. PESQUISA SOBRE
ACEITAÇÃO DE UM NOVO
PRODUTO EM UMA REDE
SOCIAL

22. FORMADA POR
ELEMENTOS
ESCOLHIDOS POR
DETERMINADO
CRITÉRIO
GRUPO DE
ELEMENTOS
INTENCIONALMENT
E ESCOLHIDOS
PARA COMPOR A
AMOSTRA
Intencional
EX. PESQUISA DE
OPINIÃO ONDE OS
ENTREVISTADOS SÃO
ESPECIALISTAS EM
DETERMINADO
ASSUNTO. NUMA
PESQUISA SOBRE
PREFERÊNCIA POR
DETERMINADO
COSMÉTICO, O
PESQUISADOR SE
DIRIGE A UM
GRANDE SALÃO DE
BELEZA E
ENTREVISTA AS
PESSOAS QUE ALI
ESTÃO

23. Por quotas

24. • CLASSIFICAÇÃO DA POPULAÇÃO DE ACORDO COM
PROPRIEDADES RELEVANTES PARA A CARACTERÍSTICA A SER
ESTUDADA
SEXO, IDADE, CLASSE SOCIAL...
• DETERMINAÇÃO DA PROPORÇÃO DA POPULAÇÃO PARA CADA
PROPRIEDADE (QUOTAS).

25. EX. SE NÓS DEFINIMOS SEGMENTOS POR SEXO NUMA
POPULAÇÃO EM QUE HÁ 60% DAS MULHERES E 40% HOMENS, E
QUEREMOS OBTER UMA AMOSTRA DE 1.000 PESSOAS,
DEFINIMOS UMA META DE 600 MULHERES E 400 HOMENS.
ESTES OBJETIVOS SÃO CONHECIDOS COMO QUOTAS. NESTE
EXEMPLO, TERÍAMOS UMA QUOTA DE GÊNERO DE 600
MULHERES E 400 HOMENS.

26. • SELEÇÃO NÃO ALEATÓRIA DE ELEMENTOS DE CADA QUOTA
IDENTIFICADA
EX. EM UM ESTUDO NO QUAL NÓS DEFINIMOS UMA QUOTA DE
100 PESSOAS COM MENOS DE 25 ANOS E 100 PESSOAS COM
IDADES ENTRE 25 ANOS OU MAIS, CASO NÃO CONSEGUIMOS
ATINGIR 100% DA QUOTA PROMETIDA, PODERÍAMOS SAIR NAS
RUAS E ABORDAR PESSOAS, ENTREVISTANDO AQUELAS QUE
CUMPREM AS IDADES RESTANTES PARA FECHAR A QUOTA
REFERENTE A NOSSA META

27. AVALIAÇÃO DAS
TÉCNICAS DE
AMOSTRAGEM
As amostras probabilísticas são preferíveis do
ponto de vista do estatístico, mas, na prática,
elas nem sempre são possíveis

28. Amostras
aleatórias
Exigem que o pesquisador tenha a
listagem com todas as unidades da
população
NA GRANDE PARTE DOS CASOS,
INVIABILIZA A TOMADA DE
AMOSTRAS ALEATÓRIAS
SIMPLES
Ex. não é possível obter uma amostra aleatória
de cariocas porque não temos uma lista com o
nome de todos os cariocas

29. • Não exige que a população
seja conhecida
Organizada em filas, arquivos
ou até mesmo em ruas
Amostras
sistemáticas

30. • Exige livre acesso aos conglomerados, o que nem
sempre acontece
Amostras por con glomerados
EX. UM MEDICO QUE SORTEAR CINCO HOSPITAIS DA CIDADE DE
SP PARA ENTREVISTAR PACIENTES COM PROBLEMAS
CARDÍACOS, MAS DIFICILMENTE IRÁ CONSEGUIR PERMISSÃO DA
DIRETORIA DE TODOS OS HOSPITAIS

31. Exige conhecimento da população, mas as unidades
não precisam estar numeradas ou identificadas
Amostras por quotas
EX. UMA AMOSTRA DE HOMENS E MULHERES EMPREGADOS DE
UMA CERTA EMPRESA, BASTA SABER A PROPORÇÃO DE
HOMENS E MULHERES NA EMPRESA E AMOSTRAR NA MESMA
PROPORÇÃO

32. MÉTODOS
TABULARES
E MÉTODOS
GRÁFICOS

33. Tabela
É um quadro que resume um
conjunto de observações
Composta de:
Título: conjunto de informações que
respondem às perguntas: O que? Quando? Onde?
Corpo: conjunto de linhas e colunas
Cabeçalho: conteúdo das colunas
Rodapé: observações pertinentes

35. Dados brutos
O conjunto dos dados numéricos obtidos
Rol
O arranjo dos dados brutos em ordem de
frequência decrescente ou crescente Ex. n = 21,
22, 23, 23, 24, 28, 33, 35
Amplitude total ou
range (R)
A diferença entre o maior e o menor valor
observado Ex. R = 35 – 21 = 14
Classe
É cada um dos grupos de valores em que se
subdivide a amplitude total do conjunto da
variável
CONCEITOS

36. Limite de classe
São os valores extremos do intervalo de cada classe
Ex. No intervalo de classe 75 |---- 85, o limite inferior
(Li) é representado por 75, incluído no intervalo, e 85
representa o limite superior (Ls), excluído do intervalo
Ponto médio do intervalo de
classe
É o valor que representa a classe para o cálculo de
certas medidas

37. É o número de vezes que o elemento aparece na amostra (ou o número de elementos em uma
classe)
FREQUÊNCIA SIMPLES ABSOLUTA ( FI )
É a soma da frequência absoluta da classe com a frequência absoluta das anteriores
FREQUÊNCIA ABSOLUTA ACUMULADA ( FAC )
Tipos de frequências

38. n = numero de observações
ÚLTIMA FAC É IGUAL AO TAMANHO DA AMOSTRA
Tipos de frequências

39. É o valor da frequência absoluta dividido pelo número total de observações
FREQUÊNCIA SIMPLES RELATIVA ( FR )
Tipos de frequências

40. É o valor da frequência acumulada dividido pelo número total de observações
FREQUÊNCIA RELATIVA ACUMULADA
Tipos de frequências

41. SIMPLES
Distribuição de frequências

42. CONJUNTO DAS OBSERVAÇÕES APRESENTADAS DE
FORMA CONTÍNUA
Intervalo de classes
CADA VALOR DO CONJUNTO PODE SER ALOCADO EM UM,
APENAS UM, DOS INTERVALOS

43. O NÚMERO DE INTERVALOS (K):
Intervalo de classes

44. PODE-SE TAMBÉM UTILIZAR A FÓRMULA DE STURGES:
Intervalo de classes

45. O TAMANHO DE CADA INTERVALO (W):
Intervalo de classes

46. Gráficos
• SÃO REPRESENTAÇÕES VISUAIS DOS DADOS
• TEM QUE SER REPRESENTADOS DE FORMA CORRETA
• SIMPLICIDADE, CLAREZA E VERACIDADE
• REPRESENTAÇÃO GRÁFICA DE UMA TABELA DE
FREQUÊNCIA

47. Histograma
UM PAR DE EIXOS CARTESIANOS
HORIZONTAL (ABCISSA): VALORES DA VARIÁVEL
VERTICAL (ORDENADAS): FREQUÊNCIAS (ABSOLUTAS OU
RELATIVAS)
EX. O CONJUNTO ABAIXO REPRESENTA AS NOTAS DO EXAME
FINAL DE UMA TURMA:

48. Gráfico em barras ou
colunas
• VERTICAIS OU HORIZONTAIS
• COMPARAÇÃO DE GRANDEZAS
• SÉRIES DE TEMPO

49. Gráficos em
linhas
Séries de tempo ou quando
um dos fatores seja o tempo
Construção simples

50. Gráficos em
setores
Gráfico de “pizza”
Valores de cada variável =
medidas dos ângulos