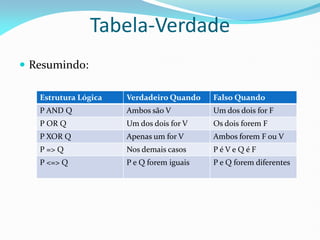
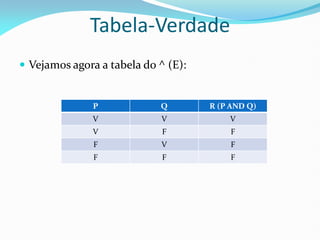
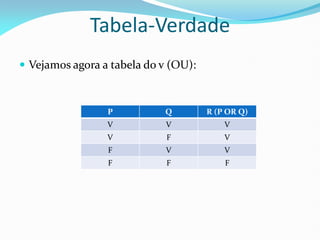
1) O documento discute lógica proposicional e conectivos lógicos, definindo proposições, argumentos e conclusões. 2) Ele explica os principais conectivos lógicos - NOT, AND, OR, XOR, => e <=> - e como eles são representados na programação. 3) Tabelas-verdade são apresentadas para cada conectivo como uma ferramenta para identificar a conclusão de proposições compostas.

1. LOGICA DE PROGRAMAÇÃO
Aula 02 - Introdução à
Lógica Matemática

2. Proposições e Conectivos
 Na área da Lógica o encadeamento de idéias é chamado de
ARGUMENTO
 Dado que um ARGUMENTO é formado por uma
seqüência de proposições/afirmações, o seu desfecho é
chamado de CONCLUSÃO e os passos anteriores são as
PREMISSAS
 A Lógica objetiva analisar se a CONCLUSÃO é uma
conseqüência lógica das PREMISSAS

3. Proposições
 A PROPOSIÇÃO é um conjunto de palavras que
exprimem um pensamento dentro de certo contexto,
podendo ser VERDADEIRO ou FALSO:
 A FMU é uma escola de ensino médio
 A FMU é uma escola de nível técnico
 A FMU é um instituto de ensino superior
 A FMU tem apenas um curso de nível superior
 A FMU tem vários campi

4.  Não são proposições:
 Interjeições
 Nossa, que prova difícil!
 Ei!
 Questões
 Você vai almoçar na cantina hoje?
 O que?
 Frases Imperativas
 Leia o livro que indiquei!
 Guarde o celular!
Proposições

5. Proposições
 Princípios das proposições:
 IDENTIDADE
 Uma poposição verdadeira é verdadeira, uma proposição falsa é
falsa (0 e 1 no computador)
 NÃO-CONTRADIÇÃO
 Uma proposição não pode ser verdadeira e falsa simultaneamente
 TERCEIRO EXCLUÍDO
 Uma proposição OU será verdadeira OU será falsa
(aprenderemos os operadores lógicos em breve)

6.  As proposições podem ser SIMPLES:
 P = todo aluno é da FMU
 Q = todos os alunos são estudiosos
 Ou COMPOSTAS:
 P = todo aluno é da FMU e estudioso
 Q = o ENEM foi difícil e muitos se deram mal
Proposições

7.  Os conectivos da lógica são:
 NOT (NÃO) na programação é !
 AND (E) na programação é &&
 OR (OU) na programação é ||
 XOR (OU exclusivo)
 => (então)
 <=> (se e somente se)
Conectivos

8.  Com mais de uma proposição podemos usar os conectivos
e formar:
 Conjunção: P AND Q
 Disjunção: P OR Q
 Disjunção Exclusiva: P XOR Q
 Condicionais: P => Q
 Bicondicionais: P <=> Q
Proposições

9. Tabela-Verdade
 Proposições lógicas compostas podem se tornar
complicadas a partir de certo ponto
 Essa ferramenta ajuda a identificarmos a conclusão de
uma proposição composta
 Vejamos agora as tabelas-verdade dos conectivos já
estudados juntamente com os exemplos no quadro para
esclarecer as dúvidas

10.  Vejamos agora a tabela do ^ (E):
P Q R (P AND Q)
V V V
V F F
F V F
F F F
Tabela-Verdade

11. Tabela-Verdade
 Vejamos agora a tabela do v (OU):
P Q R (P OR Q)
V V V
V F V
F V V
F F F

12. Tabela-Verdade
 Vejamos agora a tabela do v
(OU EXCLUSIVO):
P Q R (P XOR Q)
V V F
V F V
F V V
F F F

13.  Vejamos agora a tabela do 
(CONDICIONAL):
Tabela-Verdade
P Q R (P => Q)
V V V
V F F
F V V
F F V

14.  Vejamos agora a tabela do 
(BICONDICIONAL):
Tabela-Verdade
P Q R (P <=> Q)
V V V
V F F
F V F
F F V

15. Tabela-Verdade
 Resumindo:
Estrutura Lógica Verdadeiro Quando Falso Quando
P AND Q Ambos são V Um dos dois for F
P OR Q Um dos dois for V Os dois forem F
P XOR Q Apenas um for V Ambos forem F ou V
P => Q Nos demais casos P é V e Q é F
P <=> Q P e Q forem iguais P e Q forem diferentes

16. Exercício
 Faça uma tabela verdade para cada conectivo visto
explicando suas proposições P e Q em formato textual
também
 O formato textual precisa fazer sentido lógico em
português
 Desenhe os respectivos conjuntos matemáticos