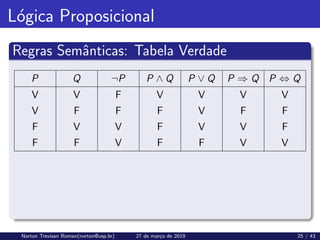
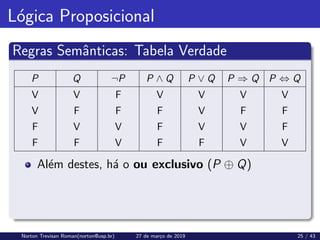
O documento aborda sistemas baseados em conhecimento, enfatizando a importância da base de conhecimento e do motor de inferência que derivam novas sentenças. Discute diferentes abordagens, como a declarativa e a procedimental, e a definição de sistemas especialistas e lógica formal. Também explora a relação de consequência lógica e suas implicações na dedução e raciocínio lógico.






































































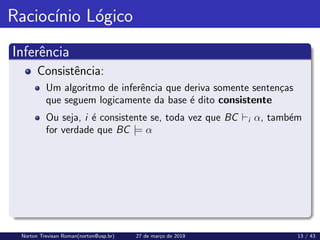

































![Lógica Proposicional
Sintaxe: Gramática formal
Sentença → Sentença Atômica | Sentença Composta
Sentença Atômica → Verdadeiro | Falso | Sı́mbolo
Sı́mbolo → P | Q | R | . . .
Sentença Composta → ( Sentença ) | [ Sentença ]
| ¬Sentença
| Sentença ∧ Sentença
| Sentença ∨ Sentença
| Sentença ⇒ Sentença
| Sentença ⇔ Sentença
Precedência de operadores: ¬, ∧, ∨, ⇒, ⇔
Norton Trevisan Roman(norton@usp.br) 27 de março de 2019 20 / 43](https://image.slidesharecdn.com/aula08-210424140133/85/ACH2044-Inteligencia-Artificial-Aula-08-107-320.jpg)
![Lógica Proposicional
Sintaxe: Gramática formal
[ ] e ( ) signifi-
cam a mesma coisa
Sentença → Sentença Atômica | Sentença Composta
Sentença Atômica → Verdadeiro | Falso | Sı́mbolo
Sı́mbolo → P | Q | R | . . .
Sentença Composta → ( Sentença ) | [ Sentença ]
| ¬Sentença
| Sentença ∧ Sentença
| Sentença ∨ Sentença
| Sentença ⇒ Sentença
| Sentença ⇔ Sentença
Precedência de operadores: ¬, ∧, ∨, ⇒, ⇔
Norton Trevisan Roman(norton@usp.br) 27 de março de 2019 20 / 43](https://image.slidesharecdn.com/aula08-210424140133/85/ACH2044-Inteligencia-Artificial-Aula-08-108-320.jpg)
![Lógica Proposicional
Sintaxe: Gramática formal
Apenas dão mais
opções para leitura
Sentença → Sentença Atômica | Sentença Composta
Sentença Atômica → Verdadeiro | Falso | Sı́mbolo
Sı́mbolo → P | Q | R | . . .
Sentença Composta → ( Sentença ) | [ Sentença ]
| ¬Sentença
| Sentença ∧ Sentença
| Sentença ∨ Sentença
| Sentença ⇒ Sentença
| Sentença ⇔ Sentença
Precedência de operadores: ¬, ∧, ∨, ⇒, ⇔
Norton Trevisan Roman(norton@usp.br) 27 de março de 2019 20 / 43](https://image.slidesharecdn.com/aula08-210424140133/85/ACH2044-Inteligencia-Artificial-Aula-08-109-320.jpg)