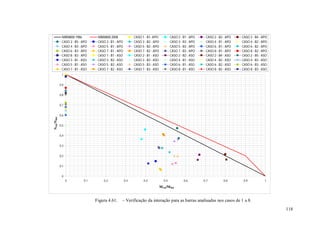
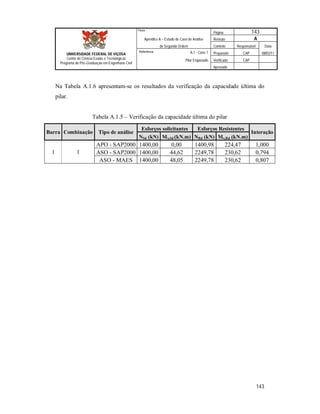
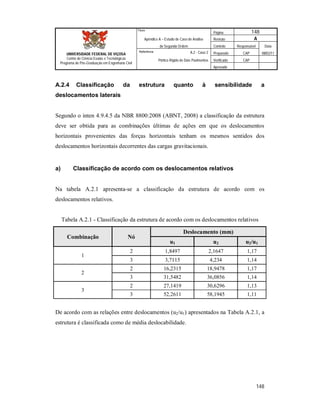
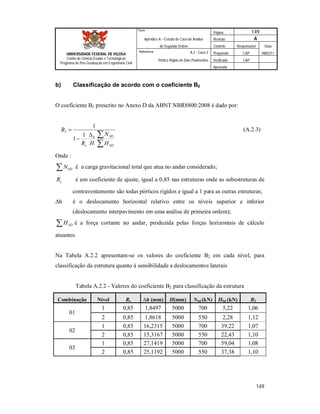
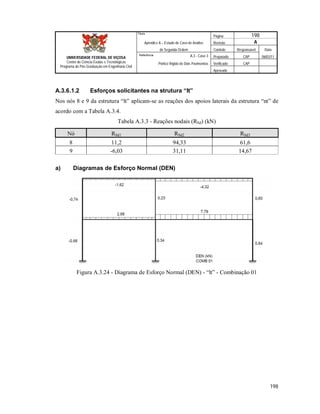
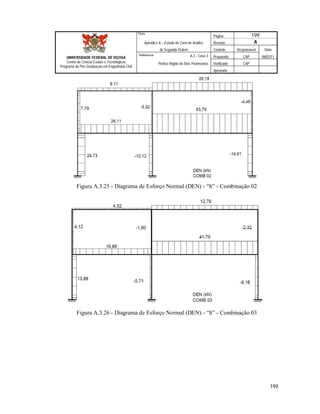
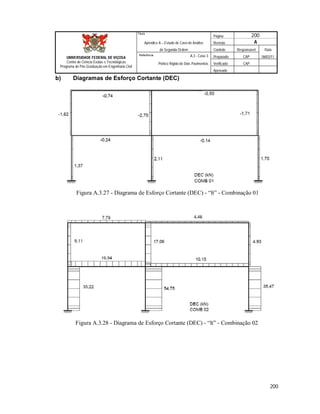
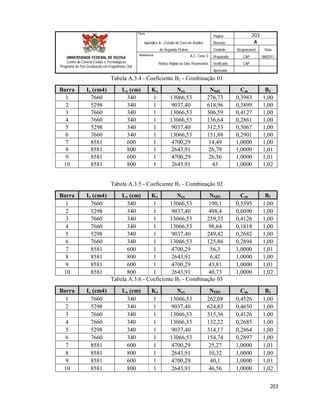
Este documento apresenta uma dissertação de mestrado sobre a avaliação da aplicação da análise de segunda ordem em pórticos de edifícios correntes em aço. O documento inclui introdução, revisão teórica, metodologia, estudos de caso, resultados e conclusões. Os estudos de caso analisam diferentes configurações de pórticos de aço submetidos à análise de primeira e segunda ordem.