Aplicação da Técnica Mapreduce na Modelagem de Algoritmos Genéticos para o “Problema do Caixeiro Viajante”

SERVIÇO PÚBLICO FEDERAL
MINISTÉRIO DA EDUCAÇÃO
INSTITUTO FEDERAL DE EDUCAÇÃO, CIÊNCIA E TECNOLOGIA DO PARÁ
TECNOLOGIA EM ANÁLISE E DESENVOLVIMENTO DE SISTEMAS
GASTÃO JOSE MACEDO CLAUDE
WESLEY LOUZEIRO MOTA
APLICAÇÃO DA TÉCNICA MAPREDUCE NA MODELAGEM
DE ALGORITMOS GENÉTICOS PARA O “PROBLEMA DO
CAIXEIRO VIAJANTE”
BELÉM
2014

1
APLICAÇÃO DA TÉCNICA MAPREDUCE NA MODELAGEM
DE ALGORITMOS GENÉTICOS PARA O “PROBLEMA DO
CAIXEIRO VIAJANTE”
.
Trabalho Acadêmico de Conclusão de
Curso apresentado ao Colegiado
Específico de TADS do Instituto Federal
de Educação, Ciência e Tecnologia do
Pará – IFPA, como requisito para a
obtenção do Grau em Tecnologia em
Análise e Desenvolvimento de Sistemas,
sob a orientação do Prof. Ms. Claudio
Roberto de Lima Martins.
BELÉM
2014

2
APLICAÇÃO DA TÉCNICA MAPREDUCE NA MODELAGEM DE
ALGORITMOS GENÉTICOS PARA O “PROBLEMA DO CAIXEIRO
VIAJANTE”
Data Defesa: ___ /___/___
Conceito:______________
Banca Examinadora
.
_______________________________________
Profº. Orientador: Msc. Claudio Roberto de Lima Martins – IFPA
_______________________________________
Profº. Msc. Fabrício Medeiros Alho – IFPA
_______________________________________
Profº. Msc. Márcio Góes do Nascimento – IFPA
BELÉM
2014

3
RESUMO
Os problemas que envolvem processamento de grandes conjuntos de
dados, tem como solução o uso do modelo do processamento paralelo e distribuído,
que se adapta a qualquer volume e nível de processamento. Esse é o caso do
MapReduce, uma técnica que abstrai os detalhes de paralelização do algoritmo de
execução para o processamento de grandes conjuntos de dados, tornando-se
adequado na aplicação dos Algoritmos Genéticos (AG), técnicas de otimização
aplicadas em domínios como inteligência artificial, otimização numérica e
combinatória. Neste trabalho é demonstrada a aplicação da técnica MapReduce na
modelagem do Algoritmo Genético para resolver o Problema do Caixeiro Viajante,
um problema que tenta determinar a menor rota para percorrer uma série de cidades
(visitando cada uma pelo menos uma vez). É realizado um levantamento das
técnicas, conceitos e modelos, e com base nisso é proposto uma nova modelagem
do Algoritmo Genético para o MapReduce na tecnologia Apache Hadoop. A proposta
é fundamentada nas melhores características apresentadas por outros modelos,
melhorando o seu desempenho e simplificando o seu desenvolvimento. A avaliação
é baseada na simulação da aplicação e no desempenho do modelo sobre a variação
do tamanho dos dados de processamento. Os resultados demonstram que o
modelo proposto é eficiente no processamento de grande quantidade de dados, pois
comprova-se que o aumento do tamanho dos dados iniciais da aplicação tende a
encontrar as melhores soluções.
PALAVRAS-CHAVE: MapReduce; Hadoop; Algoritmos Genéticos; Problema do
Caixeiro Viajante.

4
ABSTRACT
The problems involving processing of large data sets, has as solution model
of parallel and distributed processing, which adapts to any volume and level of
processing. This is the case of MapReduce, a technique that abstracts the details of
parallelization of the execution algorithm for processing of large data sets, making it
suitable in the application of Genetic Algorithms (GA) optimization techniques applied
in fields such as artificial intelligence, numerical optimization, and Combinatorics. In
this work is demonstrated the application of MapReduce technique on modeling the
genetic algorithm to solve the Travelling Salesman Problem, a problem that attempts
to determine the shortest route to traverse a series of cities (visiting each one at least
once). Is performed a survey of techniques, concepts and models, and on this basis
it is proposed a new modeling of Genetic Algorithm for the MapReduce in the Apache
Hadoop technology. The proposal is grounded on the best features presented by
other models, improving performance and simplifying its development. The
evaluation is based on simulations of application and performance of the model on
the variation of the size of the data processing. The results demonstrate that the
proposed model is efficient in processing large amounts of data, because it proves
that the increase in the size of the initial data from the application tends to find the
best solutions.
KEY-WORDS: MapReduce, Hadoop, Genetic Algorithm, Traveling Salesman
Problem

5
LISTA DE ILUSTRAÇÕES
1 Figura 2.1: Ilustração das funções de ordem-superior map e fold, e
seu funcionamento.
15
2 Figura 2.2: Vista simplificada do funcionamento de um trabalho
MapReduce.
17
3 Figura 2.3: Fluxo de uma operação do modelo MapReduce. 18
4 Figura 3.2. Shuffle e Sort em MapReduce. 32
5 Figura 4.1. Detalhe do indivíduo AG. 38
6 Figura 4.2: Grafo completo no plano Euclidiano. 42
7 Figura 4.3: Codificação da “Representação Matricial”. 45
8 Figura 4.4: Codificação “sequencial”: a) Sequência Ordenada; b)
Notação do Ciclo.
45
9 Figura 4.5: Funcionamento do operador PMX. 47
10 Figura 4.6: Funcionamento do operador CX. 48
11 Figura 4.7: Funcionamento do operador OX. 49
12 Figura 5.1: Mapa das cidades do PCVS no plano euclidiano. 55
13 Figura 5.2: Exemplo do cálculo da distância entre as cidades. 56
14 Figura 5.3: Funcionamento do processamento MapReduce para o
Algoritmo Genético no modelo Dupla Geração.
59
15 Figura 5.4: Fluxo lógico de dados do processo MapReduce para o AG. 61
16 Figura 5.5: Código Map do Algoritmo Genético MapReduce. 63
17 Figura 5.6: Código Reduce do Algoritmo Genético MapReduce. 64
18 Figura 5.7: Diagrama de classe do PCV-AG para o MapReduce. 65
19 Figura 5.8: Código simplificado da classe Indivíduo. 66
20 Figura 5.9: Código simplificado da classe CaixeiroViajanteMapper. 66
21 Figura 5.10: Código simplificado da classe CaixeiroViajanteReducer. 67
22 Figura 5.11: Código simplificado da classe OperacaoGenetica. 68
23 Figura 5.12: Mapa do conjunto de 20 cidades no plano euclidiano. 70
24 Figura 5.13: Tendência gerada pelo aumento de escala da população. 72
25 Figura 5.14: Melhor e pior indivíduo encontrado entre os melhores. 73

6
SUMARIO
1 INTRODUÇÃO ........................................................................................................................8
1.1 OBJETIVO ......................................................................................................................... 11
1.1.1 Objetivo Geral.................................................................................................................. 11
1.1.2 Objetivo Especifico.......................................................................................................... 11
1.2 METODOLOGIA................................................................................................................. 11
1.3 ESTRUTURA DO TEXTO ..................................................................................................12
2 MODELO MAPREDUCE.......................................................................................................13
2.1 INTRODUÇÃO.................................................................................................................... 13
2.2 MAPREDUCE..................................................................................................................... 16
2.2.1 Funcionamento................................................................................................................ 18
2.3 FRAMEWORK DE EXECUÇÃO MAPREDUCE................................................................ 20
2.4 IMPLEMENTAÇÃO ............................................................................................................ 21
2.4.1 Google MapReduce......................................................................................................... 21
2.4.2 Apache Hadoop............................................................................................................... 22
2.4.3 Twister ............................................................................................................................. 22
2.4.4 Phoenix............................................................................................................................ 23
2.4.5 Mars .................................................................................................................................23
2.4.6 CELL MapReduce ........................................................................................................... 24
2.4.7 MRPGA............................................................................................................................ 24
2.5 CONCLUSÃO ..................................................................................................................... 24
3 HADOOP...............................................................................................................................25
3.1 INTRODUÇÃO.................................................................................................................... 25
3.1.1 Componentes .................................................................................................................. 25
3.1.2 Modo de Execução.......................................................................................................... 26
3.2 HDFS ..................................................................................................................................27
3.3 FRAMEWORK MAPREDUCE............................................................................................ 28
3.3.1 Execução do Trabalho ....................................................................................................29
3.3.2 Partitioners e Combiners.................................................................................................30
3.3.3 Shuffle e Sort................................................................................................................... 31
3.3.4 Aplicações ....................................................................................................................... 33
3.4 CONCLUSÃO ..................................................................................................................... 35
4 AG & PCV..............................................................................................................................36
4.1 ALGORITMOS GENÉTICOS ............................................................................................. 36

7
4.1.1 Indivíduos e a População................................................................................................ 37
4.1.2 Inicialização ..................................................................................................................... 39
4.1.3 Processo de Avaliação e Seleção................................................................................... 39
4.1.4 Processo de Cruzamento e Mutação.............................................................................. 40
4.1.5 Processo de Atualização e Finalização.......................................................................... 41
4.2 PROBLEMA DO CAIXEIRO VIAJANTE ............................................................................ 41
4.2.1 Codificação...................................................................................................................... 44
4.2.2 Aptidão............................................................................................................................. 46
4.2.3 Operadores de cruzamento............................................................................................. 46
4.2.4 Operadores de mutação..................................................................................................49
4.3 CONCLUSÃO ..................................................................................................................... 50
5 IMPLEMENTAÇÃO ...............................................................................................................51
5.1 TRABALHOS RELACIONADOS........................................................................................ 51
5.2 MODELO AG EM MAPREDUCE....................................................................................... 52
5.3 MODELAGEM DO PROBLEMA ........................................................................................ 54
5.3.1 Modelagem do Algoritmo Genético................................................................................. 56
5.3.2 Modelagem do MapReduce ............................................................................................ 58
5.4 IMPLEMENTAÇÃO ............................................................................................................ 61
5.4.1 Algoritmo.......................................................................................................................... 61
5.4.2 Implementação em Java .................................................................................................65
5.5 TESTES E AVALIAÇÃO DE RESULTADOS.....................................................................69
5.5.1 Ambiente operacional e cenário de execução................................................................ 69
5.5.2 Simulações e resultados obtidos .................................................................................... 71
5.5.3 Desempenho da Modelagem Dupla Geração ................................................................ 73
5.6 CONSIDERAÇÕES FINAIS ............................................................................................... 74
CONCLUSÃO...........................................................................................................................78
REFERÊNCIAS BIBLIOGRÁFICAS .......................................................................................81
ANEXO A..................................................................................................................................84

8
1 INTRODUÇÃO
Vivemos na era dos dados. Não é fácil medir o volume total de dados
armazenados eletronicamente, mas uma estimativa da IDC (EMC, 2014) colocou o
tamanho do "universo digital" em ordem do zetabytes, fenômeno chamado de Big
Data (aqui denominado com BigData). Há uma grande quantidade de dados, a
maioria dos dados está contida nas maiores propriedades da web, ou instituições
científicas ou financeiras. A New York Stock Exchange, Facebook, Ancestry.com, O
Large Hadron Collider (LHC), trabalha ou armazena dados que vai de terabytes a
petabytes (WHITE, 2010).
Atualmente há vários exemplos de aplicações sobre o BigData. Por exemplo,
a análise dos dados sobre o comportamento do usuário web recuperados de
sistemas de vendas na web e redes sociais. O registro do comportamento gera uma
quantidade de dados que muitas organizações simplesmente não conseguem lidar
com o volume, levando ao descarte desses dados depois de algum tempo. Isto
representa perda de oportunidades. Conhecer o comportamento dos usuários
permite melhores decisões de negócios e uma vantagem competitiva no mercado.
Em termos gerais, isso é conhecido como inteligência de negócios, que abrange
uma ampla variedade de tecnologias, incluindo data warehousing, data mining e
analytics (LIN & DYER, 2010).
O BigData é um conceito definido para um conjunto de dados extremamente
grande, gerado pelo crescimento do poder computacional e do surgimento de novas
fontes geradoras de informação, tornando-se um desafio na área de Tecnologia da
Informação. O BigData deve tratar de pelo menos três propriedades: volume,
velocidade, variedade. O volume está associado ao sistema de armazenamento que
extrapola os valores tradicionais a ser armazenado. A velocidade está relacionado
ao processamento e à rapidez no acesso aos dados. A variedade diz respeito à
diversidade do formato e da estrutura de armazenamento dos dados de origem.
Portanto a solução para o BigData deve possuir a característica de
escalabilidade para suprir todas as sua propriedades. Soluções convencionais, como
banco de dados relacional, não conseguem atender questões que envolvem o
Volume e a Velocidade, pois o poder de processamento, de capacidade e

9
armazenamento é melhor resolvido no modelo do processamento paralelo e
distribuído, como o presentes em grid computacional, tornado assim adaptável a
qualquer volume em nível de processamento.
Mas, empregar o paradigma de paralelização da computação, com
distribuição dos dados, não é trivial. Aspectos envolvidos com a paralelização,
tolerância a falhas, distribuição de dados e balanceamento de carga devem ser
levados em conta pelo desenvolvedor de aplicações (DEAN & GHEMAWAT, 2008).
O programador tem que pensar nas falhas da implementação, na reprogramação e
substituição de máquinas defeituosas, coordenar os processos da computação
distribuída em larga escala, saber se um processo remoto falhou ou não, enfim, um
grande desafio a superar.
Como solução para esses problemas e desafios, foi proposto o modelo
MapReduce de programação, para ser executado em um grid computacional. Como
a solução para o BigData está relacionada com escalabilidade, MapReduce extrai a
dificuldade de programação do grid computacional, provendo suporte às
propriedades do BigData. A velocidade é resolvida com as escalabilidade do
processamento do MapReduce, baseado em cada processador dos nós que fazem
parte do grid; se houver necessidade de aumentar a velocidade de resposta, basta
aumenta o número de máquinas no arranjo do grid. O Volume é resolvido com a
escalabilidade do sistema de armazenamento distribuído do MapReduce; para mais
volume, mais máquinas podem ser adicionadas para a utilização do disco rígido em
cada nó, sem prejudicar o sistema, tornado-se bem flexível. A Variedade é resolvida
com a utilização de Banco de Dados com tecnologias específicas para o modelo,
como o NoSQL, que fornece suporte a estrutura "chave/valor", um esquema
altamente escalavel para a manipulação de grandes bases de dados em formatos
diversos.
MapReduce é um modelo de programação baseado em duas funções
chamadas map e reduce, inspiradas em linguagens funcionais. Esse modelo
estabelece uma abstração que permite construir aplicações com operações simples,
escondendo os detalhes da paralelização. Em resumo, tais funções utilizam um
conjunto de pares chave/valor para entrada e saída dos dados. O modelo
MapReduce divide o processamento em duas etapas. Na primeira o Map, mapeia e

10
distribui os dados em diversos nós de processamento e armazenamento; na
segunda etapa, o Reduce, que agrega e processa os resultados principais, para
gerar um resultado final. O poder computacional da técnica MapReduce pode ser
aplicado em vários campos, como o agrupamento de dados, aprendizado de
máquina e visão computacional. Um desses casos são os Algoritmos Genéticos na
qual tende a encontra valores de alta aptidão com o aumento na escala do número
de indivíduos da população, porém esse aumento levaria um alto custo de
processamento, tornado a técnica MapReduce ideal.
Os Algoritmos Genéticos são aplicados em vários domínios, tais como, no
campo da inteligência artificial, otimização numérica e combinatória, engenharia,
química, biologia e etc. Os Algoritmos Genéticos mais simples necessitam de uma
grande população para encontrar uma boa solução, essa grande quantidade de
dados podem afetar o desempenho da máquina, pois dependendo do problema
exigiria grande quantidade de memória e de processamento, tornando impossível
para uma só máquina. Sendo os Algoritmos Genéticos um algoritmo de natureza
paralela ele pode ser processado em várias máquinas, porém isso demandaria que
o algoritmo implementasse todas as rotinas necessárias para a paralelização em
ambiente distribuído, tornado-o mais complexo. O MapReduce é uma técnica para
abstrair os detalhes de paralelização do algoritmo de execução, tornando adequado
para a necessidade dos Algoritmos Genéticos podendo escalar grande quantidade
de indivíduos e reduzir o tempo de execução.
O Algoritmo Genético é uma técnica de otimização utilizada como um
método de busca, podendo ser aplicada em situações que o número valores ou
combinações para resolver um determinado problema são muito alto como é caso
Problema do Caixeiro Viajante (PCV), em que o número de combinações de
caminhos aumenta exponencialmente em função do número de cidades. O PCV é
um problema de otimização NP-difícil, que consiste em encontrar o menor caminho
para um caixeiro viajante que visita várias cidades apenas uma vez, e tem diferentes
aplicações, como problema de roteamento de veículos e a otimização das tarefas de
máquinas industriais.
No trabalho de Verma et al.(2009), foi proposto uma forma de modelar as
iterações dos algoritmos genéticos, porém essa modelagem tem um alto custo de

11
desempenho quando implementada na técnica MapReduce, pois essa técnica não
suporta eficientemente aplicações iterativas. Para resolver esse problema de
desempenho, foi desenvolvida novas formas de modelar os Algoritmos Genéticos
para a técnica MapReduce, com objetivo de minimizar o custo de desempenho.
1.1 OBJETIVO
1.1.1 Objetivo Geral
O objetivo deste trabalho é demonstrar o uso da técnica MapReduce na
modelagem de algoritmos genéticos. Para isso, será demonstrado a implementação
de uma aplicação que busque a otimização para a melhor solução ao problema
conhecido por "caixeiro viajante".
1.1.2 Objetivo Especifico
Pesquisar conceitos, técnicas e ferramentas para o desenvolvimento de
aplicações distribuídas para processamento paralelo e massivo de dados.
Apresentar o modelo MapReduce de programação. Demonstrar uma implementação
MapReduce para armazenamento, manipulação e análise de dados. Apresentar o
Algoritmo Genético e seu processo de funcionamento. Apresentar o conceito do
Problema do Caixeiro Viajante e os métodos dos Algoritmos Genéticos específicos
para esse problema. Demonstrar as formas de modelar os Algoritmos Genéticos e
sua implementação para Framework Hadoop. Avaliar os resultados do modelo e da
aplicação utilizada para resolver o Problema do Caixeiro Viajante.
1.2 METODOLOGIA
Neste trabalho foi feita uma pesquisa bibliográfica de documentos relevantes
sobre a tecnologia do BigData, do modelo de programação MapReduce, do
Framework Hadoop, sobre o Algoritmos Genético e, especialmente, ao problema
do "Caixeiro Viajante".

12
Depois do levantamento da técnica e conceitos, foi desenvolvida uma
modelagem para implementar o algoritmo genético no MapReduce, para resolver o
problema do "caixeiro viajante".
Foi realizada uma avaliação dos resultados obtidos na simulação da
aplicação quanto a melhor solução otimizada, considerando o tamanho da
população do AG, isto é, uma análise sobre a variação da quantidade de dados que
servem de parâmetros para busca da melhor solução.
1.3 ESTRUTURA DO TEXTO
O trabalho está organizado da seguinte forma. No capítulo 2 apresenta o
modelo de programação MapReduce, seus conceitos, características,
funcionamento e implementações. No capítulo 3 é apresentada a implementação
MapReduce, o Apache Hadoop, sua estrutura, características e componentes, em
especial o HDFS e o framwork Hadoop MapReduce. No capítulo 4, apresenta-se a
técnica do Algoritmo Genético e o Problema do Caixeiro Viajante. No capítulo 5 é
apresentada a modelagem do Algoritmo Genético no modelo de programação
MapReduce para o Problema do Caixeiro Viajante, além de sua implementação no
Apache Hadoop, e relatados os resultados obtidos na simulação do algoritmo e as
considerações finais.

13
2 MODELO MAPREDUCE
O modelo de programação MapReduce é utilizado para o processamento de
grandes conjuntos de dados. É baseado no ambiente computacional paralelo e
distribuído, provendo escalabilidade e simplificação para o desenvolvimento das
aplicações para o BigData. Embora MapReduce proporcione facilidades no
processamento do BigData, as aplicações devem se projetadas como é proposto no
modelo de programação funcional, exigindo um estudo mais detalhado sobre o
domínio da aplicação, verificando-se se ela se adéqua ao modelo MapReduce.
Este capítulo apresenta a técnica MapReduce. Na seção 2.1 é apresentada
uma visão geral do modelo. Na seção 2.2, o modelo MapReduce é definido em
termos de seu funcionamento. Na seção 2.3 apresentamos as características de
execução do MapReduce. Na seção 2.4 apresentamos as implementações do
MapReduce disponíveis no mercado. Finalizamos com a conclusão do capítulo na
seção 2.5.
2.1 INTRODUÇÃO
O MapReduce foi originalmente desenvolvido pela Google no início dos anos
2000, no qual se buscava aperfeiçoar o serviço de busca de páginas Web,
almejando criar uma melhor técnica para processar e analisar regularmente o
imenso conjunto de dados da Web (GOLDMAN et al., 2012, p. 3). Para o
processamento de grande quantidade de dados, há necessidade que o
processamento seja distribuído entre centenas ou milhares de máquinas,
configuração que permite diminuir o tempo desse processamento. As questões de
como paralelizar a computação, distribuir os dados, e identificar as falhas, dificultam
a computação simples, levando o programador a lidar com grande quantidade de
código complexo (DEAN & GHEMAWAT, 2008, p. 1).
Com o objetivo de resolver esta complexidade, Jeffrey Dean e Sanjay
Ghemawat, dois engenheiros da Google, desenvolveram a tecnologia MapReduce
inspirada nas funções map e reduce presentes na linguagem de programação Lisp e
em muitas outras linguagens funcionais. Essa nova abstração permitiu a execução

14
de algoritmos mais simples, escondendo os detalhes da paralelização, tolerância a
falhas, distribuição de dados e balanceamento de carga em uma biblioteca criada
para essa finalidade (DEAN & GHEMAWAT, 2008, p. 1). Deste modo, possibilitou
otimizar a indexação e catalogação dos dados sobre as páginas Web e suas
ligações.
O MapReduce permite dividir um grande problema em vários pedaços e
distribuí-los em diversos computadores. Essa técnica deixou o sistema de busca do
Google mais rápido mesmo sendo executado em computadores convencionais e
menos confiáveis, diminuindo assim os custos ligados à infraestrutura (GOLDMAN et
al., 2012, p. 3).
MapReduce tem suas raízes em programação funcional. Uma característica
chave de linguagens funcionais é o conceito de funções de ordem-superior (higher-
order), ou funções que podem aceitar outras funções como argumentos. Duas
funções comuns de ordem superior são map e fold. Por exemplo, dada uma lista
conforme vista na Figura 2.1, a função superior map utiliza a função f, que recebe
como parâmetros todos os elementos da lista. A lista resultante da função map é
utilizada pela função superior fold, que combina os valores da lista através da função
g. A função g usa um valor inicial e o primeiro item da lista, o resultado é
armazenado em uma variável intermediária. Na segunda execução, g utiliza a
variável intermediária e o próximo item da lista. Este processo se repete até que
todos os itens da lista tenham sido processados, retornando no final o valor da
variável intermediária (LIN & DYER, 2010, p. 20).
Podemos ver map como uma forma concisa para representar a
transformação de um conjunto de dados, como definido pela função f. Na mesma
linha, podemos ver fold como uma operação de agregação, como definido pela
função g. Uma observação imediata é que a aplicação de f para cada item em uma
lista pode ser paralelizado de uma maneira simples, uma vez que cada aplicação
funcional acontece isoladamente. Em um cluster de máquinas, estas operações
podem ser distribuídas em diferentes máquinas. A operação de fold, por outro lado,
tem mais restrições quanto à localidade dos dados, pois os elementos da lista
devem ser reunidos para serem aplicados na função g. No entanto, muitas
aplicações não exigem que a função g seja aplicada a todos os elementos da lista.

15
Na medida em que elementos na lista posam ser divididos em grupos, a função fold
também pode prosseguir em paralelo. Resumidamente, descrevemos a técnica
MapReduce, em que suas fases Map e Reduce correspondam aproximadamente às
operação map e fold da programação funcional (LIN & DYER, 2010, p. 20).
Figura 2.1: Ilustração das funções de ordem-superior map e fold, e seu
funcionamento (Adaptado de: LIN & DYER, 2010, p. 20).
Visto de um ângulo diferente, MapReduce pode ser aplicado como uma
receita genérica para processamento de grandes conjuntos de dados, organizado
em duas fases que correspondem às duas funções do MapReduce. No primeiro
estágio, uma computação é aplicada paralelamente sobre todos os registros de
entrada de um conjunto de dados, produzindo uma saída intermediária que é então
agregada por uma computação na segunda fase (LIN & DYER, 2010, p. 21).
O par chave/valor é a estrutura básica de dados no MapReduce. Os
algoritmos devem levar um conjunto de pares chave/valor de entrada e produzir um
conjunto de pares chave/valor de saída. O usuário da biblioteca do MapReduce
modela o algoritmo como duas funções Map e Reduce. O Map leva um par de
entradas e produz um conjunto de pares chave/valor intermediários, que em seguida
são agrupados de acordo com a chave e passa para a função de Reduce. A função
reduce, aceita uma chave intermediária e seu conjunto de valores. Ela mescla esses
valores para formar um conjunto possivelmente menor de valores (DEAN &
GHEMAWAT, 2008, p. 1).
f f f f f
g g g g g
Lista usada no map
Lista resultante do map
Lista usada no fold
Valor Inicial Valor Final
Variável Intermediária
Função f
Função g

16
Para ser preciso, MapReduce pode referir-se a três conceitos distintos, mas
relacionados. Primeiro, MapReduce é um modelo de programação. Segundo,
MapReduce pode referir-se ao framework de execução, que coordena a execução
de programas escritos neste estilo particular de tecnologia. Finalmente, MapReduce
pode se referir à implementação de software do modelo de programação e do
framework de execução, como é o caso das várias implementação existentes, como
a ferramenta proprietária do Google, e a solução em código aberto do Hadoop, para
processadores multicore (Phoenix) e etc. (LIN & DYER, 2010, p. 21).
2.2 MAPREDUCE
Como visto, MapReduce é um modelo de programação especificado em
funções map e reduce. Pares de chave/valor formam a estrutura básica de dados
em MapReduce. Parte do projeto de algoritmos MapReduce envolve impor a
estrutura de chave/valor em conjuntos de dados com qualquer tipo de dado (inteiro,
texto, etc). Em alguns algoritmos, as chaves de entrada não são particularmente
significativas e são simplesmente ignoradas durante o processamento, enquanto em
outros casos chaves de entrada são usados para identificar exclusivamente um dado
(LIN & DYER, 2010, p. 22).
Em MapReduce, o programador define a função map e a função reduce com
as seguintes assinaturas (onde [ e ] representam uma lista de valores) :
map: (k1, v1)  [(k2, v2)]
reduce: (k2, [v2])  [(k3, v3)]
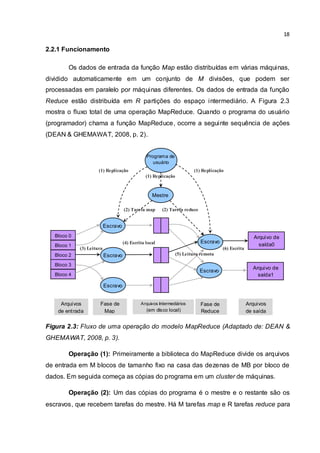
A entrada para um trabalho MapReduce começa com os dados
armazenados no sistema de arquivos distribuído. Como podemos ver na Figura 2.2,
os algoritmos devem levar um conjunto de pares chave/valor de entrada e produzir
um conjunto de pares chave/valor de saída. O usuário (programador) da biblioteca
MapReduce modela o algoritmo como duas funções Map e Reduce. O Map escrito
pelo programador leva um par de entradas e produz um conjunto de pares
chave/valor intermediários. Posteriormente, são unidos todos os valores

17
intermediários associados com a mesma chave e passa o resultado para a função
Reduce. A função Reduce, também escrita pelo programador, aceita uma chave
intermediária e seu conjunto de valores. A função Reduce mescla esses valores
para formar um conjunto possivelmente menor de valores (DEAN & GHEMAWAT,
2008, p. 1). Os dados intermediários chegam a cada redutor em ordem, classificadas
pela chave, no entanto, nenhuma relação de ordenação é garantida para chaves
através de diferentes redutores. Pares chave/valor de saída de cada redutor são
escritos persistentemente no sistema de arquivos distribuído enquanto que pares de
chave/valor intermediários são transitórios e não preservados. A saída termina em
vários arquivos no sistema de arquivos distribuído, em que corresponde ao número
de redutores (LIN & DYER, 2010, p. 22).
Figura 2.2: Vista simplificada do funcionamento de um trabalho MapReduce
(Adaptado de: LIN & DYER, 2010, p. 23).
K1 V1 K1 V1 K1 V1 K1 V1
reducer reducer reducer
K2 V2 K2 V2 K2 V2 K2 V2
K3 V3
Shuffle e Sort: Agregação de Valores por Chaves
K2 [V2] K2 [V2] K2 [V2]
mapper mapper mapper mapper
K3 V3 K3 V3

18
2.2.1 Funcionamento
Os dados de entrada da função Map estão distribuídas em várias máquinas,
dividido automaticamente em um conjunto de M divisões, que podem ser
processadas em paralelo por máquinas diferentes. Os dados de entrada da função
Reduce estão distribuída em R partições do espaço intermediário. A Figura 2.3
mostra o fluxo total de uma operação MapReduce. Quando o programa do usuário
(programador) chama a função MapReduce, ocorre a seguinte sequência de ações
(DEAN & GHEMAWAT, 2008, p. 2).
Figura 2.3: Fluxo de uma operação do modelo MapReduce (Adaptado de: DEAN &
GHEMAWAT, 2008, p. 3).
Operação (1): Primeiramente a biblioteca do MapReduce divide os arquivos
de entrada em M blocos de tamanho fixo na casa das dezenas de MB por bloco de
dados. Em seguida começa as cópias do programa em um cluster de máquinas.
Operação (2): Um das cópias do programa é o mestre e o restante são os
escravos, que recebem tarefas do mestre. Há M tarefas map e R tarefas reduce para
Arquivos
de entrada
Fase de
Map
Fase de
Reduce
Arquivos
de saída
Arquivos Intermediários
(em disco local)
Programa de
usuário
Mestre
Escravo
Escravo
Escravo
Escravo
Escravo
Bloco 0
Bloco 1
Bloco 2
Bloco 3
Bloco 4
Arquivo de
saída0
Arquivo de
saída1
(1) Replicação (1) Replicação
(1) Replicação
(2) Tarefa map (2) Tarefa reduce
(4) Escrita local
(3) Leitura (6) Escrita
(5) Leitura remota

19
ser atribuído, o mestre escolhe as máquinas ociosas e atribui a cada um delas uma
tarefa map ou reduce.
Operação (3): O escravo que executa uma tarefa map lê o conteúdo do
bloco de entrada e analisa os pares chave/valor encontrados, passando-os para a
função map definida pelo usuário. A função map produz os pares chave/valor
intermediários, que são armazenados em buffer na memória.
Operação (4): Periodicamente, os pares em buffer são gravados no disco
local, dividido em R regiões pela função de particionamento. Os endereços desses
pares no disco local são passados para o mestre, que é responsável por encaminhar
esses endereços para os escravos reduce.
Operação (5): Quando um escravo reduce é notificado pelo mestre sobre
esses endereços, ele usa chamadas de procedimento remoto para ler os dados do
disco local de cada escravo map. Quando um escravo reduce tem que ler todos os
dados intermediários para sua partição, ele classifica os dados pela chave para que
todos os valores que têm a mesma chave sejam agrupados juntos.
Operação (6): O escravo reduce itera sobre os dados classificados e para
cada chave intermediária única, ele passa a chave e o conjunto correspondente de
valores intermediários para a função reduce do usuário. A saída da função de
reduce é anexada a um arquivo de saída final para cada partição do reduce.
Operação (7): Quando todas as tarefas map e reduce forem concluídas, o
mestre reativa o programa do usuário para a recuperação do resultado final.
Após a conclusão, a saída da execução do MapReduce está disponível em
R arquivos de saída. Normalmente, os programadores não precisam combinar esses
arquivos em um único arquivo, pois muitas vezes eles são usados como entrada
para outra trabalho MapReduce ou são usados para outro aplicativo distribuído
(DEAN & GHEMAWAT, 2008, p. 3).
Para cada tarefa map e reduce, o mestre armazena o estado (ocioso, em
andamento ou concluído) e a identidade da máquina escravo. O mestre é o canal
através do qual a localização das regiões de arquivo intermediário é transferida das
tarefas map para as tarefas reduce. Antes, para cada tarefa map concluída, o mestre

20
armazena os endereços e os tamanhos das regiões de arquivo intermediário
produzidos pela tarefa map. Essas informações são recebidas quando as tarefas
map são concluídas e é enviada incrementalmente para o escravo que tem em
andamento as tarefas reduce (DEAN & GHEMAWAT, 2008, p. 3).
2.3 FRAMEWORK DE EXECUÇÃO MAPREDUCE
O MapReduce separa os algoritmos de execução dos detalhes do
sistema paralelo e distribuído, como a distribuição de dados, o balanceamento de
carga, o tratamento de falhas entre outros. Um programa MapReduce, é referido
como um trabalho (work), consistindo em um código para fase Map, um código para
fase Reduce e mais os parâmetros de configuração. O desenvolvedor envia o
trabalho para um nó mestre do cluster e o framework de execução (runtime) cuida
de tudo (LIN & DYER, 2010, p. 26).
Cada trabalho MapReduce é dividido em unidades menores chamadas de
tarefas (job). Existem trabalhos que têm milhares de tarefas que precisam ser
atribuídas ao cluster. Em muitos casos o número das tarefas é maior que o número
de máquinas em um cluster, levando o framework definir a ordem de prioridade de
execução das tarefas. A ideia do MapReduce é mover o código e não os dados. O
agendador de tarefas localiza as máquinas que têm os dados para ser processados,
se isso não for possível, as novas tarefas serão iniciadas em outros lugares e os
dados necessários serão transmitidos através da rede (LIN & DYER, 2010, p. 26-
27).
Em MapReduce , a sincronização é realizada entre a fases Map e Reduce. A
tarefa reduce não pode começar antes que todas as emissões dos pares chave/valor
das tarefas map tenham sido concluídas e que todos os pares chave/valor
intermediários tenham sido transferidos, agrupados e classificados (LIN & DYER,
2010, p. 27-28).
O framework de execução MapReduce deve realizar todas as tarefas
anteriores em um ambiente onde os erros e falhas são frequentes. A biblioteca
MapReduce é projetada para tolerar falhas de máquina com elegância em uma

21
ambiente de centenas ou milhares de máquinas. Para lidar com falhas das máquinas
escravas, o mestre se comunica com todos os escravos periodicamente, se
nenhuma resposta for recebida em um determinado período de tempo, o mestre
marca o escravo como “falho”. Com isso, qualquer tarefa map ou reduce em
andamento é reagendamento para outra máquina (DEAN & GHEMAWAT, 2008, p.
3).
2.4 IMPLEMENTAÇÃO
Implementação MapReduce pode se referir a implementação de software do
modelo de programação e do framework de execução. Muitas implementações
diferentes do modelo de programação MapReduce são possíveis, dependendo
somente do ambiente (DEAN & GHEMAWAT, 2008, p. 2). Já existem várias
implementações do modelo, mantendo ou não a mesma abstração básica, mas suas
capacidades variam consideravelmente. Entre elas foram desenvolvidas várias
implementações de código fonte aberto, mantido pela comunidade de software livre,
destacando-se o Apache Hadoop, que é utilizado neste trabalho.
2.4.1 Google MapReduce
Google MapReduce é uma implementação proprietária da Google, projetado
em C++ podendo executar aplicações escritos em várias linguagens de
programação. Essa implementação do MapReduce é direcionada para o ambiente
de computação da Google feito por grandes aglomerados de PCs. O GFS (Google
File System) é um sistema de arquivos distribuído desenvolvido pela Google, é
usado para gerenciar os dados armazenados sobre os discos rígidos do grid
computacional. O sistema de arquivos usa replicação para fornecer disponibilidade e
confiabilidade em cima de hardware não confiável. O programador envia trabalhos
para um sistema de agendamento e cada tarefa do trabalho é mapeado pelo
agendador para um conjunto de máquinas disponíveis dentro de um cluster (DEAN
& GHEMAWAT, 2008, p. 2).

22
2.4.2 Apache Hadoop
Apache Hadoop é uma implementação de código aberto do MapReduce
implementado em Java, que permite o processamento distribuído e o
armazenamento de grandes conjuntos de dados em clusters de computadores de
máquinas comuns. Ele fornece um sistema de arquivos distribuído (HDFS) que
armazena dados sobre os nós do cluster, proporcionando elevada largura de banda
agregada em todo o cluster. Hadoop MapReduce pode executar aplicações
implementada em várias linguagem, podendo ser escrita em Java , Ruby , Python e
C++.
As tecnologias MapReduce e Hadoop Distributed File System são projetadas
para detectar e lidar com falhas na camada de aplicação, entregando um serviço
altamente disponível em ambiente propenso a falhas. Outros projetos de código
aberto para uma proposta específica foram construídos com Hadoop, na qual foram
incorporados ao seu ecossistema, tornando uma infraestrutura cada vez mais
completa (HADOOP, 2014).
A aplicação Hadoop em um aglomerado de máquinas utiliza cinco
componentes diferentes, o NameNode, o DataNode, o SecondaryNameNode, o
JobTracker e o TaskTracker. O NameNode gerencia os arquivos de metadados
armazenados no HDFS, como a estrutura de diretório de arquivos e a localização
das cópias dos blocos de dados. O DataNode é o responsável pelo armazenamento
dos dados no HDFS. O SecondaryNameNode fornece backup e compactação de
metadados do sistema de arquivos. O JobTracker fornece comando e controle para
o gerenciamento do trabalho, lidando com a distribuição e gerenciamento das
tarefas. O TaskTracker fornece serviços de execução para as tarefas MapReduce,
gerenciando a execução no cluster e executando as tarefas Map e as tarefas
Reduce.
2.4.3 Twister
Twister é uma implementação em Java de código aberto e uma extensão do
MapReduce otimizado para computação iterativa. O Twister usa uma infraestrutura

23
de mensagens, publicação/assinatura, para a comunicação e transferência de dados
e suporta longa duração de tarefas map e reduce. Além disso, fornece uma
extensão de programação para o MapReduce, permitindo o Twister suportar
computação MapReduce iterativa, isso é feito através do adicionamento de uma
nova fase para o MapReduce chamado "Combine", que atua como um outro nível de
redução, pode ser usada para produzir uma saída coletiva a partir de todas as
saídas da fase reduce (EKANAYAKE et al., 2010, p. 1).
2.4.4 Phoenix
O Phoenix é uma versão do MapReduce implementada em C e de código
aberto, direcionado para sistemas multicore e multiprocessadores simétricos de
memória compartilhada. Em contraste com o sistema MapReduce original que foi
projetado para clusters, o Phoenix usa threads de memória compartilhada para
implementar o paralelismo. A implementação lança vários threads de trabalho para
executar as funções map e reduce do usuário (YOO et al., 2009, p. 2). Phoenix
consiste em uma API (bibliotecas) para a programação de aplicativo e um
framework que lida com a paralelização, gerenciamento de recursos e de
recuperação de falhas. A implementação do Phoenix fornece uma API para C e C++.
(RANGER et al., 2007, p. 3).
2.4.5 Mars
Mars é uma implementação MapReduce para processadores gráficos
(GPUs). Mars explora grande quantidades threads paralelo dentro da GPU, esconde
a complexidade de programação da GPU por trás da interface MapReduce. Mars
fornece um pequeno conjunto de APIs, implementadas em C/C++, para os
desenvolvedores que não requer nenhum conhecimento de renderização gráfica (HE
et al., 2008, p. 4-5).

24
2.4.6 CELL MapReduce
Cell MapReduce é uma implementação do modelo MapReduce escrito em C
para processador Cell. Este modelo fornece uma abstração para máquina simples,
escondendo a paralelização e o hardware. A arquitetura Cell é uma arquitetura de
memória distribuída, é um projeto de alto nível que se assemelha ao projeto do
Google, enquanto a granularidade das operações é semelhante ao Phoenix. O
modelo de programação é adequado a vários programas de dados paralelos,
mapeando naturalmente para a arquitetura Cell (KRUIJF & SANKARALINGAM,
2007).
2.4.7 MRPGA
Uma extensão para o MapReduce para paralelização automática de
Algoritmos Genéticos com a programação sequencial através de três componentes:
Map, Reduce, e Reduce, chamado MRPGA (MapReduce for Parallel Genetic
Algorithms). A aplicação do usuário pode ser implementado em C++, C# e Visual
Basic, ou com qualquer linguagem suportada pela plataforma “.NET” (JIN et al.,
2008, p. 1-6).
2.5 CONCLUSÃO
MapReduce é um modelo de programação para o processamento de
grandes conjuntos de dados em ambiente computacional paralelo e distribuído. O
paradigma é poderoso, mas simples o suficiente para o desenvolvimento das
aplicações BigData. Além disso, existe uma variedade de implementação, algumas
de código fonte aberto para diversos ambientes e propósitos.
Para testar o modelo de programação MapReduce apresentaremos no
próximo capítulo a implementação MapReduce de código aberto Apache Hadoop,
demonstrando suas características, estrutura e funcionamento.

25
3 HADOOP
O Apache Hadoop, ou simplesmente Hadoop, é uma ferramenta para
processamento de grande quantidade de dados em aglomerados computacionais,
disponibilizando recursos para o desenvolvimento de soluções em sistemas paralelo
e distribuídos em um único arcabouço.
Este capítulo descreve o Apache Hadoop, suas características, estrutura e
funcionamento. Na seção 3.1 é apresentando uma visão geral da ferramenta. Na
seção 3.2 é demonstrado o sistema de arquivos distribuído HDFS. Na seção 3.3,
demonstra-se o framework Hadoop MapReduce, suas características e execução,
finalizando com uma conclusão na seção 3.4.
3.1 INTRODUÇÃO
Hadoop é um implementação MapReduce de código aberto, escrito em Java
para o processamento e armazenamento em larga escala, utilizando máquinas
comuns, sendo seus principais componentes o Framework MapReduce e o Hadoop
Distributed File System (HDFS).
Hadoop permite o processamento distribuído e o armazenamento de
grandes conjuntos de dados em clusters de computadores, fornecendo um sistema
de arquivos distribuído que armazena dados sobre os nós de computação,
proporcionando elevada largura de banda agregada em todo o cluster. O Framework
MapReduce e Hadoop Distributed File System (HDFS) são projetados para detectar
e lidar com falhas na camada de aplicação, entregando um serviço altamente
disponível em ambiente propenso a falhas (HADOOP, 2014).
3.1.1 Componentes
A aplicação Hadoop em um aglomerado utiliza cinco componentes
(daemons) diferentes. Três deles, o NameNode, o DataNode e o
SecondaryNameNode, compõem o sistema de arquivos HDFS; os outros dois
componentes, o JobTracker e o TaskTracker, integram o framework MapReduce.

26
O NameNode gerencia os arquivos de metadados armazenados no HDFS
incluindo informações críticas, como a estrutura de diretório de arquivos e a
localização das cópias dos blocos de dados do arquivo. A máquina que executa o
processo do servidor NameNode é o mestre HDFS (VENNER, 2009, p. 73).
O DataNode realiza o armazenamento dos dados no HDFS. Como o HDFS
é um sistema de arquivos distribuído, necessita diversas instâncias do DataNode.
Cada DataNode fornece serviços de armazenamento em blocos para o HDFS
(VENNER, 2009, p. 73).
O SecondaryNameNode fornece backup e compactação de metadados do
sistema de arquivos fornecendo backup quase em tempo real dos metadados para o
NameNode. Há pelo menos um caso deste servidor executando em um cluster. O
NameNode secundário também mescla o histórico de alterações de metadados, o
log de edição, na imagem do sistema de arquivos do NameNode (VENNER, 2009, p.
73).
O JobTracker fornece comando e controle para o gerenciamento do
trabalho. Ele também lida com a distribuição e gerenciamento de tarefas. Há uma
instância desse servidor executando em um cluster. A máquina que executa o
servidor JobTracker é o mestre MapReduce (VENNER, 2009, p. 72).
O TaskTracker fornece serviços de execução para a tarefa MapReduce.
Cada TaskTracker gerencia a execução de tarefas em um nó do cluster. Um
TaskTracker executa uma tarefa Map ou uma tarefa Reduce designada a ele. Há
uma instância do TaskTracker por nó escravo no cluster (VENNER, 2009, p. 72).
3.1.2 Modo de Execução
Há três modos de execução: Modo Local, Modo Pseudo Distribuído e Modo
Completamente Distribuído.
Modo Local (Standalone Mode) é a configuração padrão de execução do
Hadoop. Não existem daemons sendo executados e tudo é executado em uma única
Máquina Virtual Java (JVM). Nessa configuração, todo o processamento da

27
aplicação é executado apenas na máquina local, não sendo necessário usar o HDFS
para armazenar os arquivos. Esse modo é adequado para a execução de programas
MapReduce durante o desenvolvimento, uma vez que é mais fácil de testar e
depurar.
Modo Pseudo Distribuído (Pseudo Distributed Mode) é o modo no qual são
aplicadas todas as configurações necessárias para execução em um aglomerado,
porém os daemons do Hadoop são executados na máquina local, simulando assim
um aglomerado de pequena escala.
Modo Completamente Distribuído (Fully Distributed Mode) é o modo no qual
os daemons do Hadoop rodam em um cluster de máquinas. Este modo é utilizado
para o processamento distribuído da aplicação Hadoop em um aglomerado real.
3.2 HDFS
Quando um conjunto de dados supera a capacidade de armazenamento de
uma única máquina física, torna-se necessário particioná-lo através de um número
de máquinas separadas. Sistemas de arquivos que gerenciam o armazenamento
através de uma rede de máquinas são chamados de sistemas de arquivos
distribuído (WHITE, 2010, p. 41).
O HDFS é um sistema de arquivos distribuído projetado para armazenar de
forma confiável grandes conjuntos de dados e para proporcionar alta tolerância a
falhas, funciona em grandes aglomerados de máquinas comuns, destinado ao
armazenamento e transmissão de arquivos de centenas de Megabytes a Terabytes
de dados. O HDFS fornece acesso de alta taxa de transferência de dados adequado
para aplicações que têm grandes conjuntos de dados (WHITE, 2010, p. 41-42).
HDFS utiliza o conceito de bloco, cujo tamanho padrão é de 64 MB. Como
em um sistema de arquivos tradicionais, os arquivos no HDFS são quebrados em
pedaços de blocos, que são armazenados como unidades independentes.
Entretanto, quando um arquivo for menor do que um único bloco, o espaço restante
do bloco poderá ser utilizado. O beneficio que o bloco de abstração traz para um
sistema de arquivos distribuído é que um arquivo pode ser maior do que qualquer

28
disco único na rede. Além disso, os blocos se encaixam bem com a replicação para
fornecer tolerância a falhas e disponibilidade. Para evitar problemas com os blocos
corrompidos e disco e falha da máquina, cada bloco é replicado para um pequeno
número de máquinas fisicamente separado (WHITE, 2010, p. 43-44).
Um cluster HDFS tem dois tipos de nó que operam em um padrão de
mestre/escravo. Possui um nó mestre chamado NameNode, e uma série de
escravos chamados DataNodes. O NameNode gerencia o espaço de nomes do
sistema de arquivos, mantém as informação da árvore de arquivos e dos metadados
no disco local. O NameNode também conhece os DataNodes onde todos os blocos
dos arquivos estão localizados. DataNode armazenam e recuperam blocos quando é
solicitado e apresentam um relatório ao NameNode periodicamente com listas de
blocos que estão sendo armazenado (WHITE, 2010, p. 44).
Sem o NameNode, o sistema de arquivos não pode ser usado, pois os
arquivos seriam irrecuperáveis. Por esse motivo, o Hadoop proporciona dois
mecanismos para fazer a NameNode resistente a falhas, através do backup ou
SecondaryNameNode .
O primeiro mecanismo é fazer backup dos arquivos que compõem o estado
persistente de metadados do sistema de arquivos. Hadoop pode ser configurado
para que o NameNode grave seu estado de persistente para múltiplos sistemas de
arquivos.
O segundo mecanismo é por execução de um NameNode secundário
chamado de SecondaryNameNode, que age diferente do NameNode. O seu
principal papel é mesclar periodicamente a imagem namespace com o log de
edição. Ele mantém uma cópia da imagem namespace mesclado, que pode ser
usado em caso de falha do NameNode (WHITE, 2010, p. 44-45).
3.3 FRAMEWORK MAPREDUCE
Um dos principais componente do Hadoop é um framework para
processamento paralelo e distribuído de grandes conjuntos de dados para grandes
aglomerados computacionais. Permite a execução de tarefa simples, escondendo os

29
detalhes da paralelização, tolerância a falhas, distribuição de dados e
balanceamento.
3.3.1 Execução do Trabalho
Há quatro entidades independentes na execução do trabalho MapReduce: o
cliente, que envia o trabalho de MapReduce; o JobTracker, que coordena a
execução do trabalho; os TaskTrackers, que executam as tarefas do trabalho que foi
dividido; e, o sistema de arquivos distribuídos HDFS, que é usado para o
compartilhamento de arquivos de trabalho entre as outras entidades (WHITE, 2010,
p. 167).
O processo de execução do trabalho MapReduce no Hadoop é feito através
das seguintes etapas: processo de envio do trabalho, inicialização, atribuição e
execução de tarefa e a conclusão do trabalho MapReduce. Esses passos são
explicados a seguir.
Envio de Trabalhos: O processo de submissão solicita ao JobTracker um
novo ID de trabalho, em seguida verifica a especificação de saída do trabalho e
calcula as divisões de entrada para o trabalho. Os recursos necessários para
execução do trabalho são copiados, incluindo o arquivo JAR do trabalho, o arquivo
de configuração, e as divisões de entrada, para o sistema de arquivos do
JobTracker. E no final indica ao JobTracker que o trabalho está pronto para
execução (WHITE, 2010, p. 167-169).
Inicialização do Trabalho: Quando o JobTracker recebe uma chamada de
submissão de trabalho, ele coloca o trabalho em uma fila interna onde o agendador
de tarefas vai buscá-lo e inicializá-lo. A inicialização envolve a criação de um objeto
para representar o trabalho que está sendo executado, que encapsula as tarefas e
informações para o acompanhamento do seu status e progresso. Para criar a lista
de tarefas a serem executadas, o agendador de tarefas recupera primeiro as
divisões de entrada do sistema de arquivos compartilhado. Em seguida, cria uma
tarefa map para cada divisão de entrada, e o número de tarefas reduce é definido
pelo agendador (WHITE, 2010, p. 169).

30
Atribuição de tarefas: Tasktrackers executam um loop simples que envia
periodicamente chamadas Heartbeats1
para o JobTracker. O Heartbeats funcionam
como um canal de mensagens que dizer ao JobTracker que uma TaskTracker está
ativo. Como parte dos Heartbeats, o TaskTracker vai indicar se ele está pronto para
executar uma nova tarefa. Tasktrackers tem um número fixo de slots2
para as tarefas
map e para tarefas reduce, podendo executar tarefas map e reduce
simultaneamente. O agendador padrão preenche os slots vazios com as tarefas map
antes das tarefas reduce (WHITE, 2010, p. 169).
Execução de Tarefas: Após a atribuição da tarefa no TaskTracker, o
próximo passo é a execução da tarefa. Para isso ele deve localizar a aplicação
"JAR", copiando do sistema de arquivos compartilhado para o sistema de arquivos
do TaskTracker. Em seguida, ele deve criar um diretório de trabalho local para a
tarefa, e criar uma instância de TaskRunner para execução dela. TaskRunner lança
uma nova JVM para executar cada tarefa, de modo que todos os erros da aplicação
map e reduce do usuário não afetem o TaskTracker (WHITE, 2010, p. 170).
Conclusão do trabalho: Quando o JobTracker recebe uma notificação de
que a última tarefa para um trabalho é concluído, ele muda o status do trabalho para
"sucesso". Se o trabalho foi concluído com êxito, o usuário é informado e
posteriormente o JobTracker limpa o estado de funcionamento do trabalho e instrui
TaskTrackers a fazer o mesmo (WHITE, 2010, p. 172-173).
3.3.2 Partitioners e Combiners
Existem dois elementos adicionais que completam o modelo de
programação: Partitioners (particionadores) e Combiners (combinadores).
Partitioners são responsáveis por dividir as chaves intermediárias e atribuir
os pares chave/valor intermediário para as tarefas reduce, ou seja, especifica para
onde o par chave/valor intermediário deve ser copiado. Dentro de cada tarefa
reduce, as chaves são processadas em ordem de classificação. O Particionador
1
São “sinais de vida” para verificar se o componente hadoop está “vivo”.
2
São espaços para armazenamento e execução das tarefas.

31
mais simples envolve calcular o valor Hash da chave e, em seguida, tomar o resto
da divisão (mod) desse valor com o número de tarefas reduce, ou seja, hash(key)
mod R. Isso atribui aproximadamente o mesmo número de chaves para tarefas
reduce (LIN & DYER, 2010, p. 28-29).
Combiners são uma otimização no MapReduce que permite a agregação
local. O combinadores é como se fosse um “mini-reducers” que ocorrem na saída da
fase Map, antes da fase shuffle e sort (especificado em seguida) podendo reduzir o
número de pares de chave/valore intermediários, tonando mais eficiente, pois os
pares de chave/valor precisam ser copiados em toda a rede, tornado a troca de
dados mais rápido. Cada combinador opera isoladamente e, portanto, não tem
acesso a saída intermediária de outras funções map. O combinador recebe os pares
chave/valore associados a cada chave. O combinador pode emitir qualquer número
de pares chave/valor, mas o seu tipo deve ser o mesmo da saída da fase Map, pois
se o combinador não ocorrer, a saída da função map será a entrada da função
reduce (LIN & DYER, 2010, p. 29).
3.3.3 Shuffle e Sort
MapReduce garante que a entrada para cada reduce é classificada por
chave. O processo pelo qual o sistema executa a classificação (Sort), e transfere
das saídas do map para a entrada do reduce, é conhecido como o Shuffle. De certa
maneira, o shuffle é o coração do MapReduce (WHITE, 2010, p. 177).
Na fase Map quando a função map começa a produzir a saída, não é
simplesmente gravado no disco. O processo é mais complexo, é tira proveito de
buffer, escrevendo na memória e fazer algumas pré-classificação por razões de
eficiência como pode se visto na Figura 3.1. Cada tarefa map tem um buffer de
memória circular na qual é escrito sua saída. O buffer é de 100 MB por padrão, um
tamanho que pode ser alterado. Quando o conteúdo da memória intermediária
atinge um determinado tamanho começará a transferência (spill) do conteúdo para o
disco. A saída map continuará sendo escrito no buffer, enquanto o spill acontece,
mas se o buffer enche durante este tempo, o map irá bloquear até que o spill estiver
completo (WHITE, 2010, p. 177).

32
Figura 3.1. Shuffle e Sort em MapReduce (WHITE, 2010, p.178).
Antes de gravar no disco, ocorre uma divisão dos dados em partições
(partition) correspondentes aos reduce. Em cada partição é executada uma
classificação (sort) por chave na memória, e se existe uma função Combiner, esta é
executada usando saída da classificação. Para cada spill um novo arquivo é criado,
então no fim da tarefa map pode haver vários arquivos Spill. Antes que a tarefa seja
concluída, os arquivos Spill são mesclados (merge) em um único arquivo de saída
dividido e classificado. Se a função combinadora for especificada, o número de spill
será menor, reduzindo assim o espaço em disco, e a quantidade de dados a ser
transferida para o reduce (WHITE, 2010, p. 178).
Na fase Reduce, o arquivo de saída map é armazenado no disco local do
TaskTracker que executou a tarefa map, mas agora é necessário pelo TaskTracker
que executará as tarefas de reduce. Além disso, a tarefa reduce precisa das
partiçãos específicas das saídas map de todas as tarefas map do cluster. As tarefas
map podem terminar em momentos diferentes, por isso a tarefa reduce começará a
copiar os seus resultados, assim que cada um é concluído. Isto é conhecido como a
fase de cópia da tarefa reduce (WHITE, 2010, p. 179).
As saídas de map são copiados para a memória do TaskTracker Reduce, se
forem pequenas o suficiente, se não, são copiados para o disco. Quando o buffer de
memória atinge um tamanho limite, ou atinge um limite do número de saídas de

33
map, os dados são fundidos e transferidos (Spill) para o disco. Como as cópias são
acumuladas no disco, é feito antecipadamente a fusão (merge) em um grande
arquivo ordenado (WHITE, 2010, p. 179).
Quando todas as saídas map forem copiadas, a tarefa reduce passa para a
fase de classificação, que funde as saídas map, mantendo a sua ordem de
classificação. A fusão salva em um caminho para o disco, alimentando diretamente a
função reduce, que é a última fase, a fase reduce. Durante a fase de redução, a
função reduce é chamada para cada chave da saída classificada. A saída resultante
dessa fase é escrito diretamente no sistema de arquivos de saída, geralmente o
HDFS. Neste caso o nó do TaskTracker também executará um DataNode (WHITE,
2010, p. 179-180).
3.3.4 Aplicações
A aplicação MapReduce do Hadoop usa uma biblioteca do MapReduce (API)
que está no pacote org.apache.hadoop.mapreduce e outras do pacote
org.apache.hadoop, como o subpacote io e fs.Path além das API do próprio Java. A
aplicação deve ter as classes que representam as funções map e reduce, uma
classe principal (Drive) e as classes auxiliares da lógica de execução.
Ao invés de usar tipos Java, Hadoop fornece seu próprio conjunto de tipos
básicos que são otimizados para serialização de rede. Estes se encontram no
pacote org.apache.hadoop.io.
Hadoop usa seu próprio formato de serialização de dados, através da
interface Writables. Essa interface define dois métodos, o write() para escrever o
seu estado no fluxo binário pelo DataOutput, e o readFields() para a leitura de seu
estado no fluxo binário pelo DataInput. Qualquer chave ou valor do framework
MapReduce Hadoop implementa essa interface. Hadoop vem com uma grande
variedade de classes de Writable, na qual possui implementação para quase todos
os tipos primitivos do Java, conforme a Tabela 3.1.

34
Tabela 3.1: Representação do tipo primitivo Java em implementação do Writable.
Tipo Primitivo do Java Implementação Writable
boolean BooleanWritable
byte ByteWritable
int IntWritable
long LongWritable
float FloatWritable
double DoubleWritable
Além do que estão na Tabela 3.1 há várias outras implementações, como os
tipos: Text, um Writable para sequencias UTF-8; NullWritable, um tipo que tem uma
serialização de comprimento zero; ObjectWritable, para propósito geral. É possível
escrever uma implementação personalizada tendo o controle sobre a representação
binária e a ordem de classificação (WHITE, 2010, p. 96-97).
A função map é representada por uma classe derivada da classe abstrata
Mapper, que é encontrada no pacote org.apache.hadoop.mapreduce. A classe
abstrata Mapper é um tipo genérico, que lhe permite trabalhar com qualquer tipo de
chave ou valor, os quatro parâmetros especificam a chave de entrada, valor de
entrada, a chave de saída e valor de saída (WHITE, 2010, p. 20-21).
Essa classe declara quatro métodos, o setup, o map, o cleanup e o run, que
pode ser usada pela aplicação do usuário. O framework primeiro chama o método
setup() que é executado uma vez no início da tarefa, em seguida é chamado o
método map() para cada par chave/valor da divisão de entrada. Finalizando com a
chamada do método cleanup() que é executado uma vez no fim da tarefa. O método
run() é utilizado para ter um controle mais completo sobre a execução do Mapper.
A função reduce é representada por uma classe derivada da classe abstrata
Reducer, um tipo genérico semelhante ao Mapper que se encontram no mesmo
pacote. O Reducer tem quatro parâmetros que são usados para especificar o tipo de
entrada e saída da função reduce. Os tipos de entrada da função reduce devem
coincidir com os tipos de saída da função de map. A classe Reducer tem quatro
métodos, o setup, o reduce, o cleanup e o run, três são semelhantes ao do Mapper.

35
O framework executa os métodos da mesma forma que é executado na tarefa map,
porém o método reduce() é chamado uma vez para cada chave.
Os parâmetros de configuração do trabalho são efetuados na classe
principal (Drive), onde são definidos os caminhos de entrada e saída dos arquivos,
as classes Mapper, Reducer, Combiner e Partitioner, os tipos de saída e entrada,
além disso, é efetuado o controle, a execução e monitoramento do trabalho.
3.4 CONCLUSÃO
Hadoop é uma implementação MapReduce de código aberto, utilizado para
o processamento e armazenamento em larga escala, utilizando máquinas comuns, e
traz simplicidade para o desenvolvimento e execução de aplicação paralelo e
distribuídos. Os principais componente são o Hadoop Distributed File System o
Framework MapReduce que dão suporte a execução da aplicação MapReduce. No
capítulo seguinte apresentaremos a base teórica do Algoritmo Genético (AG) e do
Problema do Caixeiro Viajante (PCV) para a modelagem de uma aplicação
MapReduce.

36
4 AG & PCV
O Algoritmo Genético (AG) é uma técnica de otimização utilizada como
busca global, empregada em situações nas quais o número de valores ou
combinações aplicáveis para resolver um determinado problema é muito alto
(BRYANT, 2000; MISHRA, 2011; PACHECO, 1999). Este é o caso do Problema do
Caixeiro Viajante (PCV), em que o número de combinações de caminhos aumenta
exponencialmente em função do número de cidades.
O PCV é um problema de otimização que consiste em encontrar o menor
caminho em um conjunto de cidades, sendo utilizada em pesquisas e aplicações de
diferentes áreas, como da matemática, da engenharia e ciência da computação.
Para essa classe de problema não existe recurso computacional para resolvê-lo em
tempo hábil, tornando a utilização de método de força bruta difícil, necessitando o
uso de técnica de busca, como o caso dos Algoritmos Genéticos que não necessita
explorar todas as soluções possíveis para encontrar uma boa solução.
Este capítulo apresenta a técnica do Algoritmo Genético e o Problema do
Caixeiro Viajante, apresentando uma visão geral e seus conceitos. Na seção 4.1 é
definida a técnica do Algoritmo Genético e as características dos Operadores
Genéticos. Na seção 4.2 é apresentado o Problema do Caixeiro Viajante seus
conceitos e métodos AG particulares. Finalizando, na seção 4.3 com as
considerações do capítulo.
4.1 ALGORITMOS GENÉTICOS
Algoritmos Genéticos (AG) são técnicas de otimização baseadas na
evolução natural. Essas técnicas incluem a ideia da sobrevivência do mais apto em
um algoritmo de pesquisa, que não necessita explorar todas as soluções possíveis
no espaço de busca para obter um bom resultado (BRYANT, 2000, p. 2).
O AG usa um processo evolutivo para criar uma população de possíveis
respostas para um problema, em seguida, combina as melhores soluções criando
uma nova geração de soluções que devem ser melhor do que a geração anterior.

37
Este processo é constituído pelas seguintes etapas:
a) Inicialização: é a criação da população inicial para o primeiro ciclo do
algoritmo; a criação é geralmente realizada de forma aleatória.
b) Avaliação: avalia-se a aptidão das soluções analisando sua resposta
ao problema proposto.
c) Seleção: indivíduos são selecionados para a reprodução; a seleção é
baseada na aptidão dos indivíduos.
d) Cruzamento: características das soluções escolhidas são
recombinadas, gerando novos indivíduos.
e) Mutação: características dos indivíduos resultantes do processo de
reprodução são alteradas.
f) Atualização: os indivíduos criados nesta geração são inseridos na
população.
g) Finalização: verifica se as condições de encerramento da evolução
foram atingidas.
Inicialmente deve ser definido o conceito para "indivíduo", encontrando a
melhor codificação adequada para a solução do problema. A população inicial é
então selecionada, geralmente de forma aleatória, calculando-se a aptidão de cada
indivíduo. Esta aptidão é usada para encontrar os indivíduos para cruzamento, e
recombinados para criar novos indivíduos que são copiados para a nova geração.
Alguns indivíduos são escolhidos ao acaso para sofrer mutação. Após esse
processo, uma nova geração é formada e o processo é repetido até que algum
critério de parada tenha sido atingido. Neste ponto, o indivíduo que está mais
próximo do ideal é decodificado e o processo é concluído (BRYANT, 2000, p. 2-3).
4.1.1 Indivíduos e a População
Os indivíduos codificam possíveis soluções do espaço de busca de um
problema. A representação dessas soluções define a estrutura do cromossomo3
a
3
Segundo Pacheco (1999) o cromossomo é uma estrutura de dados que representa uma das possíveis
soluções do espaço de busca do problema.

38
ser manipulado, e depende do tipo de problema e do que se deseja manipular pelo
algoritmo genético.
O AG usa nomenclatura relacionada com os termos que podemos encontrar
na biologia. O indivíduo do AG, de acordo com a Figura 4.1, é composto de um ou
mais cromossomo e um valor adaptativo associado (fitness). O cromossomo é uma
cadeia de caracteres codificada de parâmetros. Normalmente, um indivíduo contém
apenas um cromossomo, que representa o conjunto de parâmetros chamados de
genes. O gene (ou caractere) é a versão codificada de um parâmetro do problema a
ser resolvido. O alelo é o valor que um gene pode assumir e o lócus é a posição que
gene ocupa no cromossomo (ALBA, 1999, p. 3).
Figura 4.1. Detalhe do indivíduo AG (ALBA, 1999, p. 4).
A população é um conjunto de indivíduos candidatos à solução do problema,
ela é uma parte do espaço de busca de um problema. O tamanho da população irá
depender do problema (HUANG & LIN, 2010, p. 5).
A população possui como características o número de geração, o grau de
convergência, a diversidade e o elitismo. O número de geração é quantas vezes a
população passa pelo processo de seleção, reprodução, mutação e atualização. O
grau de convergência representa a aproximação da média de adaptação da geração
atual em relação a anteriores. A diversidade mede o grau de variação entre os
indivíduos presentes na população; ela é fundamental para a amplitude da busca. O
baixo valor da diversidade está vinculado ao fenômeno de convergência prematura,
isto é, quando a população converge e não consegue sair de uma média de
adaptação sub-ótima (ótima local). O elitismo é composto pelos indivíduos mais
adaptados da população, onde são sempre mantidos a cada geração (LUCAS, 2002,
p. 9).

39
4.1.2 Inicialização
A inicialização da população de um AG determina o processo de criação dos
indivíduos para o primeiro ciclo do algoritmo. Geralmente, a população inicial é
formada a partir de um conjunto de indivíduos aleatoriamente criados, com o objetivo
de fornecer maior diversidade, para garantir uma boa abrangência do espaço de
busca.
Existem várias alternativas ao método randômico, destinadas a suprir
deficiências na criação aleatória de indivíduos de representação mais complexa,
algumas técnicas são: Inicialização Randômica Uniforme, em que cada gene do
indivíduo é um valor do conjunto de alelos, sorteado de forma aleatoriamente
uniforme; Inicialização Randômica não Uniforme, em que os valores do gene tendem
a ser escolhidos com uma frequência maior do que o restante; e na Inicialização
Randômica Com “Dope”, no qual os indivíduos otimizados são inseridos em meio à
população aleatoriamente gerada (LUCAS, 2002, p. 10-11).
4.1.3 Processo de Avaliação e Seleção
A avaliação é feita através de uma função que representa o problema,
fornecendo uma medida de aptidão para cada indivíduo na população. A função de
aptidão indica a qualidade de um indivíduo para solução do problema. Em muitos
casos, calcular o grau de adaptação dos indivíduos pode ser uma tarefa complexa, e
se levarmos em conta que esta operação é massivamente repetida ao longo do
processo de evolução, seu custo pode ser consideravelmente alto (LUCAS, 2002, p.
12).
No algoritmo genético, o processo de seleção escolhe os melhores
indivíduos para o cruzamento, baseada na aptidão dos indivíduos, efetuando-se um
sorteio, onde os mais aptos possuem maior probabilidade de serem escolhidos para
a reprodução, perpetuando-o para a próxima geração, mantendo as boas
características da espécie.

40
A seleção opera de forma determinística, isto é, um indivíduo só consegue
sobreviver em um ambiente se for capaz de se reproduzir, de acordo com suas
características, de responder de forma adequada a todos os fenômenos de seu
meio. A seleção também é cumulativa, pois os benefícios do processo de seleção
são mantidos de uma geração para a outra (LUCAS, 2002, p. 12).
Existem vários métodos para efetuar a seleção, dentre os quais se
destacam: a seleção por Ranking, onde os indivíduos da população são ordenados
de acordo com seu valor de aptidão, sendo os melhores ranqueados (os mais aptos)
os escolhidos para a próxima geração. A seleção por Giro de Roleta, onde é
atribuída uma probabilidade para cada indivíduo em função do seu valor de aptidão;
os que possuem as maiores possibilidades são os escolhidos a passar para a
próxima geração. Seleção por Torneio, em que grupos de soluções são escolhidos
aleatoriamente e os indivíduos mais aptos dentro de cada grupo são selecionados
para ficar para a próxima geração. E a seleção Uniforme, em que todos os
indivíduos possuem a mesma probabilidade de serem selecionados.
4.1.4 Processo de Cruzamento e Mutação
O cruzamento (crossover) é um mecanismo de recombinação de soluções. É
o processo fundamental dos AG, que possibilita a troca e manipulação de material
genético entre indivíduos trazendo melhoria para sua população. O cruzamento
consiste na escolha de dois indivíduos, resultante do processo de seleção, que são
combinados para permitir a criação de um ou mais indivíduos filhos. Há vários
métodos de escolha de pares para o cruzamento, que pode ser por escolha
aleatória, escolha entre indivíduos semelhantes ou entre indivíduos diferentes.
A mutação é realizada após o cruzamento. Baseado em uma probabilidade
predeterminada, é feita uma escolha aleatória de um indivíduo, em seguida, é
escolhido aleatoriamente um ponto ou uma parte do cromossomo do indivíduo para
fazer mutação.
A mutação é um operador exploratório, responsável por provocar pequenas
alterações genéticas nos indivíduos, permitindo ampliar o espaço de busca do

41
problema, na tentativa de chegar a soluções possíveis na qual o operador de
cruzamento não encontraria. As principais funções da mutação é a inserção de
novas características e a reposição de material genético perdido nos outros
processos, aumentando assim a diversidade na população.
4.1.5 Processo de Atualização e Finalização
Os indivíduos resultantes do processo de cruzamento e mutação são
inseridos na população de acordo com a técnica de atualização adotada pelo AG,
gerando assim uma nova população. Essa técnica determina o critério de
substituição dos indivíduos de uma população para a próxima geração.
Segundo Pacheco (1999), a atualização pode ser feita pela troca de todos os
indivíduos da população anterior pelos novos indivíduos gerados, ou ainda, a troca
de toda a população com elitismo, ou seja, o indivíduo mais apto da população
anterior é mantido na nova população. Outra técnica elitista é a troca parcial da
população em que são gerados novos indivíduos para substitui os piores indivíduos
da população anterior, permitindo ou não a presença de indivíduos duplicados.
O último passo é realizado por um teste que observa se algum critério de
parada foi satisfeito, finalizando o processo de evolução. Nos AGs, o critério de
parada pode ser: pelo número de gerações que corresponde ao total de ciclos de
evolução de um AG; pelo total de indivíduos, que é o total de tentativas em um
experimento, ou seja, o produto do tamanho da população pelo número de
gerações; e pelo grau de convergência da população, ou seja, o grau de
proximidade dos valores da avaliação de cada indivíduo da população.
4.2 PROBLEMA DO CAIXEIRO VIAJANTE
O Problema do Caixeiro Viajante (PCV), no inglês Traveling Salesman
Problem (TSP), é um problema de otimização NP-difícil mais estudada. Sua
popularidade se deve ao fato que PCV é fácil de formular, apesar de difícil solução,
tem um grande número de aplicações, tais como problema de roteamento de

42
veículos, a reformulação de motores de turbinas em aeronaves e otimização das
tarefas de máquinas industriais (GUTIN, 2009, p. 1). O PCV consiste em encontrar o
menor caminho para um caixeiro viajante que, dado um conjunto de cidades, deve
visitar todas elas precisamente uma vez, com exceção à cidade de origem na qual
deve ser feito o retorno.
Tem duas versões do PCV, o simétrico e o assimétrico. O PCV Simétrico
(PCVS) é um grafo completo não direcionado com pesos nas arestas, como pode
ser visto na Figura 4.2. O PCV Assimétrico (PCVA) é um grafo direcionado completo,
também com pesos sobre suas arestas, cujo objetivo é encontrar um ciclo
Hamiltoniano de peso mínimo, ou seja, que a soma dos pesos das arestas do ciclo
seja o menor possível. Um ciclo Hamiltoniano em um grafo e é frequentemente
chamado de tour (turnê ou caminho).
Figura 4.2: Grafo completo no plano Euclidiano.
O PCVA tem o número de caminhos possíveis dada pela fórmula ,
onde n é o número de cidades e o PCVS tem o número de caminhos igual a
, pois a direção do caminho não importa (GUTIN, 2009, p. 1). Nos dois
casos o número de caminhos possíveis para n cidades é muito grande, quase
exponencial como se pode ver na Tabela 4.1. A utilização do método de força bruta,
que examina todos os passeios possíveis, torna-se impraticável mesmo para
instâncias de problemas de tamanho moderado.

43
Tabela 4.1: Números possíveis de caminho em função do número de cidades no
problema do caixeiro viajante simétrico (PCVS).
Número
de
cidades
Número
de
caminhos
Escala
Número
de
cidades
Número de caminhos Escala
3 1 13 239.500.800
4 3 14 3.113.510.400 Bilhões
5 12 15 43.589.145.600
6 60 16 653.837.184.000
7 360 17 10.461.394.944.000 Trilhões
8 2.520 Mil 18 177.843.714.048.000
9 20.160 19 3.201.186.852.864.000 Quatrilhões
10 181.440 20 60.822.550.204.416.000
11 1.814.400 Milhões 21 1.216.451.004.088.320.000 Quintilhões
12 19.958.400 22 25.545.471.085.854.720.000
O PCV Euclidiana é um caso especial de PCVS em que os vértices são
pontos no plano euclidiano e o peso em cada aresta é a distância euclidiana entre os
seus terminais, conforme é visto na Figura 4.2. Se os vértices de um grafo
representar um conjunto de cidades e a distância euclidiana for calculada em um
sistema de coordenadas cartesianas, então a distância entre duas cidades i e j é
dada pela equação (4.1), onde cada cidade é representada por uma coordenada (x,
y).
Para resolver o PCV é necessário conhecer as distâncias entre todas as
cidades. Os métodos de resolução podem ser divididos em duas grandes classes:
Algoritmos Exatos e Heurísticas PCV ou Algoritmos de Aproximação PCV.
Algoritmos Exatos são métodos para resolver o problema PCV, ou seus
casos especiais para otimização, quando queremos obter um passeio ideal. Isto não
pode ser possível, se o algoritmo exigir tempo de execução de várias horas ou dias.

44
Heurísticas PCV ou Algoritmos de Aproximação PCV é aplicado se houver
alguma garantia de aproximação, aplicado quando o tempo de execução for limitado
ou os dados não são exatos (GUTIN, 2009, p. 4).
O AG é uma técnica de otimização que pode ser empregada no caso do
PCV. Para isso, é necessário definir a representação da solução, a função que
avalia a aptidão das soluções gerada pelo algoritmo e os operadores genéticos para
gerar novas soluções, preservando as condições inerentes do problema. Tais
questões são detalhadas a seguir.
4.2.1 Codificação
No problema do caixeiro viajante a solução (indivíduo) é codificada em uma
lista sequenciada de n cidades a serem visitadas. As cidades (gene) são
representadas pelos caracteres de um alfabeto válido. Esta lista de cidades é o
cromossomo do algoritmo genético, representando uma cadeia de caracteres. Além
da forma básica de codificação binária, também pode ser usada uma sequência de
letras, de números inteiros ou qualquer sequência de símbolos, desde que a
decodificação tenha algum significado para o problema.
A codificação conhecida como Representação Matricial é um dos métodos
usado para codificação de um caminho do problema do caixeiro viajante. A partir de
um problema envolvendo um grafo é preciso codificar uma lista de auxílio, conforme
é visto na Figura 4.3. Essa lista é uma matriz que é criada pela seguinte condição:
se houver aresta entre o nó i ao nó j, a matriz recebe 1 (um) na posição (i,j), caso
contrário recebe 0 (zero). Poderíamos, então, usar a matriz ou concatenar suas
linhas para criar uma longa sequência de zeros e uns (BRYANT, 2000, p. 10-11).

45
Figura 4.3: Codificação da “Representação Matricial”.
Outro método é o sequenciamento de caracteres4
de duas maneiras
diferentes, conforme é visto na Figura 4.4. O primeiro (a) é uma Sequência
Ordenada (C1, C2,...,Cn) o que implica que o caminho vai de C1 a C2 seguindo a
ordem até Cn, e retornando para C1. A segunda (b) maneira de representar o
problema do caixeiro viajante é com a Notação do Ciclo (Cycle Notation), com uma
cadeia de caracteres (C1, C2,..., Cn), no qual o caminho é feito indo da cidade i para
cidade Ci, até formar um ciclo (BRYANT, 2000, p. 11).
Figura 4.4: Codificação “sequencial”: a) Sequência Ordenada; b) Notação do Ciclo.
4
Em Bryant (2000) os caracteres são números inteiro, mas se usar outros tipos de caracteres indexados com
um número inteiro funciona da mesma forma.
D
A
B
C
Caminho
Sequência: C1 C2 C3 C4 índice: A=1, B=2, C=3, D=4
a)
Caminho codificado: ACBD
A  C  B  D
C1  C2  C3  C4
b)
(C1, C2, C3, C4) = (C, D, B, A)
Caminho codificado: CDBA
A  C  B  D
1 3 2 4
C4 ↘ C1 ↘ C3 ↘ C2
A  C C B B  D D A
i  Ci i  Ci i  Ci i  Ci
1 C1 3C3 2 C2 4 C4
C D B A
A C B D
Trajetória do Caminho
Trajetória do Caminho
D
A
B
C
i
j
A B C D
A 0 0 1 0 A  C
B 0 0 0 1 B  D
C 0 1 0 0 C  B
D 1 0 0 0 D  A
Caminho codificado: 0010.0001.0100.1000
Caminho Lista de auxílio Trajetória do Caminho

46
4.2.2 Aptidão
A avaliação do indivíduo é realizada através de uma função que representa
o problema, fornecendo uma medida de aptidão para cada indivíduo da população.
A função de avaliação para problema PCV deve encontrar o peso do ciclo
Hamiltoniano sobre um grafo do problema, ou seja, a soma dos pesos de todas as
arestas do ciclo. Sendo o peso de cada aresta a distância entre duas cidades, então
o peso (custo) de cada caminho é distância total percorrida pelo caixeiro viajante ao
visitar todas as cidades, conforme a equação (4.2). Quanto menor o custo
(distância), maior será a aptidão de um cromossomo (caminho) e, portanto melhor
será a solução. O objetivo do PCV, portanto, é encontrar uma solução de menor
custo (distância).
O custo de uma solução (C1, C2,..., Cn) é dado por (4,2), onde n e o número
de cidades e d(Ci, Cj) é a distância entre as cidades Ci e Cj.
4.2.3 Operadores de cruzamento
Vários métodos de cruzamento foram desenvolvidos para o problema do
caixeiro viajante. Esses operadores devem preservar a condição de que todas as
cidades devem ser visitadas exatamente uma vez, e sua função deve aplicar
permutações de valores, pois o problema PCV é de natureza combinatória.
O operador de Cruzamento de Mapeamento Parcial (PMX), do inglês
Partially Mapped Crossover, primeiramente seleciona aleatoriamente dois pontos de
corte nos cromossomos pais, conforme é visto na Figura 4.5, no qual formam a
seção de mapeamento. Em seguida, é feito o mapeamento entre os genes das
seções a partir de suas posições, então os genes dos cromossomos dos pais são
trocados de acordo com o mapeamento, ou seja, se o mapeamento for feito entre x
e y então onde houver x será trocado por y e vice-versa. Assim os pais 1 e 2 forma
respectivamente os filhos 1 e 2.

47
Figura 4.5: Funcionamento do operador PMX.
Este cruzamento é mais adequado quando é usado com a representação da
Notação do Ciclo, pois preserva mais da estrutura dos pais, ou seja, mais arestas
são transferidas para os filhos. No entanto, esta representação pode obter caminhos
ilegais, necessitando elaborar uma rotina de reparo para criar caminhos legais
(BRYANT, 2000, p. 12-13).
O operador Cycle Crossover (CX) cria descendentes cujas posições são
ocupadas por elementos correspondentes de cada um dos pais, conforme é visto na
Figura 4.6. Inicialmente é feito a escolha do primeiro gene de um dos pais, para
permanecer no cromossomo; assim, o próximo gene que permanecerá no primeiro
cromossomo será o correspondente do gene atual no segundo cromossomo, de
acordo com sua posição. Dessa forma, se o gene atual for x e seu correspondente
for y, então o y do primeiro cromossomo permanecerá. Esse procedimento ocorre
até retornar ao gene inicial. Completando o ciclo, as posições que não passaram
pelo processo são preenchidas com os genes correspondentes do outro
cromossomo, sendo este procedimento válido para os dois pais.
D  J
E  A
F  B
Mapeamento
Pai 1  ABC | DEF | GHIJ
Pai 2  GHI | JAB | EFCD
Seção de mapeamento
Pontos de corte
Pai 2  GHI | JAB | EF C D
DEF AB J
Filho 2  GHI | DEF | AB C J
Filho 1: EFCJABGHID
Filho 2: GHIDEFABCJ
Pai 1  AB C | DEF | GHI J
EF JAB D
Filho 1  EF C | JAB | GHI D

48
Figura 4.6: Funcionamento do operador CX.
Este cruzamento é mais adequado com a representação de Sequência
Ordenada. Este processo assegura que cada cromossomo seja legal, porém é
possível que a herança genética dos pais acabe. Isso não é um problema, pois
geralmente só ocorre se os pais tiverem alta aptidão, podendo ainda ser uma boa
escolha (BRYANT, 2000, p. 14).
O operador Order Crossover (OX) parte da escolha de dois pontos de corte
e reorganiza o resto dos genes para gerar um caminho válido, conforme é visto na
Figura 4.7. Um filho é criado com a seção de um dos cromossomos, completando a
parti do segundo ponto de corte, com os genes do outro cromossomo a partir do
mesmo ponto, exceto com os genes que se repete na seção inicial. Este mesmo
processo é feito para o segundo filhos com a seção do cromossomo do segundo pai.
Pai 1: ABCDEFGHIJ
Pai 2: GHIJABEFCD
ABCDEFGHIJ
GHIJABEFCD
ABCDEFGHIJ
GHIJABEFCD
ABCDEFGHIJ
GHIJABEFCD
ABCDEFGHIJ
GHIJABEFCD
Filho 1: AHIJEBGFCD
Filho 1:
Inicio do ciclo Fim do ciclo Cruzamento
ABCDEFGHIJ
GHIJABEFCD
Filho 2: GBCDAFEHIJ
Filho 2:
ABCDEFGHIJ
GHIJABEFCD
ABCDEFGHIJ
GHIJABEFCD
ABCDEFGHIJ
GHIJABEFCD

49
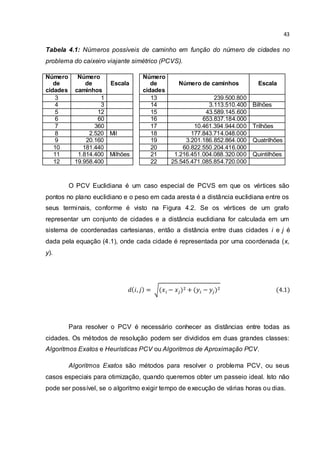
Figura 4.7: Funcionamento do operador OX.
Este cruzamento é mais adequado quando é usado com a representação de
Sequência Ordenada, pois preserva mais as estruturas ordenadas dos
cromossomos dos pais, promovendo assim a herança genética.
Além desses, existem outros operadores que se aplicam ao problema do
caixeiro viajante, como o operador Matrix Crossover (MX), um operador que usar a
representação matricial, e o Modified Order Crossover (MOX), que é semelhante ao
operador OX, mas com apenas um ponto de corte (BRYANT, 2000, p. 15-16).
4.2.4 Operadores de mutação
Há vários operadores de mutação apropriados para problemas de
permutações de valores, até operadores de mutação heurística apropriados para o
problema do caixeiro viajante.
Alguns operadores de mutação que podem ser usados são: por inserção,
deslocamento, intercâmbio recíproco e por inversão. A mutação por inserção é
quando há uma seleção aleatória de uma cidade e sua inserção em uma posição
aleatória. A mutação por deslocamento é quando selecionamos um subcaminho e
insere-o em uma posição aleatória. Temos também intercâmbio recíproco onde há
uma escolha de duas cidades aleatórias e há uma troca de posição. O operador de
inversão é uma forma diferente de mutação, que consiste na escolha aleatória de
Pai 1  ABC | DEF | GHIJ
Pai 2  GHI | JAB | EFCD
1º 2 º
XXX | DEF | XXXX
[EF]C[D]GHIJAB  CGHIJAB
JABDEFCGHI
Filho 1:
XXX | JAB | XXXX
GHI[JAB]CDEF  GHICDEF
DEFJABGHIC
Filho 2:

50
dois pontos de inversão no cromossomo e em seguida, inverte-se a ordem dos
genes entre os dois pontos.
Há também operadores de mutação heurística como os operadores 2-opt, 3-
opt e Or-opt, que efetuam a recombinação de arestas (subcaminho) se a condição
de redução do custo for satisfeita. A diferença entre esses operadores é o número
de arestas que sofrem a mutação (BRYANT, 2000, p. 18).
4.3 CONCLUSÃO
Algoritmo Genético é uma técnica para busca global, ideal para problema,
como o Problema do Caixeiro Viajante, que tem um espaço de busca muito grande.
O próximo capítulo apresenta a modelagem do Algoritmo Genético no
modelo de programação MapReduce para o Problema do Caixeiro Viajante e sua
implementação para o Hadoop.

51
5 IMPLEMENTAÇÃO
Os Algoritmos Genéticos possuem características que não permitem ser
exatamente expressa no modelo MapReduce. Para resolver esse problema, foi
desenvolvido formas de modelar o AG usando a proposta original da técnica
MapReduce. O uso da técnica MapReduce no AG proporciona uma alta capacidade
de encontrar um bom resultado em um espaço de busca extremamente grande,
podendo resolver problemas complexos como o do PCV.
Este capítulo apresenta a modelagem do Algoritmo Genético no modelo de
programação MapReduce para o Problema do Caixeiro Viajante. Na seção 5.1 é
feita uma análise dos modelos proposto por outros autores para a modelagem do
AG. Na seção 5.2 são comparadas as formas e características das modelagens
proposta e de outros possíveis modelos. Na seção 5.3 é demonstrada a modelagem
do AG para o problema do caixeiro viajante no MapReduce e seu funcionamento.
Na seção 5.4 são apresentadas as características da implementação do algoritmo
para Hadoop. Na seção 5.5 são relatados os resultados obtidos na simulação do
algoritmo. Finalizando com as considerações finais na seção 5.6.
5.1 TRABALHOS RELACIONADOS
A técnica MapReduce permite fácil desenvolvimento de aplicações
distribuídas, porém muitas aplicações não podem ser exatamente expressa com
MapReduce devido suas características. É o caso das aplicações de natureza
iterativa, pois não segue o padrão de duas fases do MapReduce (JIN et al., 2008, p
1).
Segundo Ekanayake et al. (2010), MapReduce pode ser aplicada em vários
campos, como agrupamento de dados, aprendizado de máquina e visão
computacional, onde muitos algoritmos iterativos são comuns, como é caso dos
Algoritmos Genéticos. Entretanto, para criar as iterações em uma implementação
MapReduce é necessário a execução de várias tarefas MapReduce, porém isso
gera múltiplos acessos ao sistema de arquivos distribuído, provocando um alto custo
de desempenho.

52
Considerando que a técnica MapReduce não fornece suporte eficiente para
as aplicações iterativas, algumas melhorias foram propostas com o uso de
extensões, como o Twister (EKANAYAKE et al., 2010) , o HaLoop (BU et al., 2010) e
o MRPGA (JIN et al., 2008), implementações que modificam o modelo original para
poder implementar a iteratividade.
Sendo o Algoritmo Genético uma aplicação iterativa, autores apresentaram
pesquisas para modelar o AG usando a proposta original da técnica MapReduce. No
trabalho de Verma et al.(2009) foi definido que cada iteração do AG fosse uma tarefa
MapReduce separada em que as funções map executassem as operações de
avaliação, e as funções reduce o restante das outras operações. Essa mesma
modelagem é utilizada no trabalho de Huang & Lin (2010), na implementação de um
AG para resolver o problema Job Shop Scheduling Problem5
(JSSP), com objetivo
de demonstrar o impacto do tamanho da população no resultado e no tempo de
convergência. Outro trabalho que usa a mesma modelagem é de Er & Erdogan
(2014), que avalia a aplicação dos Algoritmos Genéticos para resolver o Problema
do Caixeiro Viajante usando o framework MapReduce Hadoop; essa mesma linha de
pesquisa é utilizada também por Mishra (2011).
No trabalho de Keco & Subasi (2012) é apresentado um modelo de
paralelização de Algoritmo Genético usando o Hadoop. O modelo usa apenas uma
tarefa MapReduce para todas as iterações do AG e também concentra todo o seu
processamento na função map, reduzindo a quantidade operação de
leitura/gravação no HDFS. Esse modelo foi comparado com o modelo apresentado
em Verma et al.(2009), ambos usando o problema OneMax6
.
5.2 MODELO AG EM MAPREDUCE
Ao contrário da modelagem proposta por Verma et al.(2009), a modelagem
deste trabalho propõe que as iterações do AG sejam criadas em uma única tarefa
MapReduce, semelhante ao apresentado por Keco & Subasi (2012). Isso minimiza o
acesso ao sistema de arquivos distribuído, reduzindo o custo de desempenho, pois
5
Problema de Sequenciamento de Tarefas.
6
Problema para maximizar o número de variáveis com o valor 1 (um) em uma String Binária.

53
as iterações do algoritmo ocorrem sobre a memória principal das máquinas
presentes na rede de computadores. Na Tabela 5.1 são demonstradas as possíveis
formas de se criar as gerações da iteração do AG, com as gerações locais e globais
criadas respectivamente pela iteração na função map e reduce.
Tabela 5.1: Possíveis formas de modelagem do AG para o MapReduce.
Modelagem
do AG
Iteração
(Gerações)
Map Combiner Partitioner Reduce
Proposta por
Verma et
al.(2009)
Por tarefa
MapReduce
separada
Avaliação
da Aptidão
Não é
utilizado
Modificado
para partição
randômico
Seleção,
Cruzamento
e Mutação
Proposta de
Verma
modificado
Gerações
Globais Na
função
Reduce
Avaliação
da Aptidão
Não é
utilizado
Padrão ou
modificação
se
necessário
Seleção,
Cruzamento,
Mutação e
Avaliação
Proposta de
Keco & Subasi
(2012)
Gerações
Locais na
função Map
Avaliação,
Seleção,
Cruzamento
e Mutação
Não é
utilizado
Padrão Seleção
Combiner Gerações
Locais na
função
Combiner
Avaliação
da Aptidão
Seleção,
Cruzamento,
Mutação e
Avaliação
Padrão Seleção
Dupla
Geração
Gerações
Locais &
Globais
Avaliação,
Seleção,
Cruzamento
e Mutação
Não é
utilizado
Padrão ou
modificação
se
necessário
Seleção,
Cruzamento,
Mutação,
Avaliação
Conforme é visto na Tabela 5.1, a modelagem proposta por Verma et
al.(2009) define que cada geração do AG é feita em uma única tarefa MapReduce,
mas como pretende-se que todas as gerações sejam criadas em uma única tarefa
MapReduce esse modelo é inadequado. Entretanto, modificando esse modelo para
que as gerações fossem criadas na fase Reduce não aproveitaria todo o poder do
processamento distribuído, acarretando mais tempo para convergência.
Para ter mais aproveitamento do sistema distribuído, podem ser usadas
iterações na fase Map para criar gerações, como proposto por Keco & Subasi
(2012). Isso pode ser feito com as técnicas de agregação local Combiner ou In-
Mapper Combining (LIN & DYER, 2010), porém essa abordagem não aproveitaria a
diversidade da população que estaria em outras subpopulações. Portanto, para
aproveitar todo o poder computacional do MapReduce e a diversidade da população
é proposta a modelagem Dupla Geração, que cria gerações locais na fase Map,e
gerações globais na fase Reduce.

54
A modelagem de Dupla Geração cria paralelamente várias gerações em
uma única tarefa MapReduce. Há dois tipos de gerações, as gerações locais criada
na fase map e as gerações globais, criadas na fase reduce. As gerações locais
podem ser criadas pela função Combiner, porém o Hadoop não garante quantas
vezes o Combiner é aplicado, ou se é mesmo aplicado. A alternativa é que as
gerações locais sejam criadas pela função map, através da técnica In-Mapper
Combining, na qual incorpora as funcionalidades do Combiner diretamente dentro da
função map. As gerações globais são criadas pela função reduce que usa uma
subpopulação composta por vários indivíduos provenientes de diferentes gerações
locais.
Na modelagem do fluxo de dados proposta por Verma et al.(2009), a chave
é representada pelo indivíduo (cadeia de cidades a serem visitadas), e o valor pela
aptidão do indivíduo, que corresponde à distância percorrida no caminho. O fluxo de
dados proposto neste trabalho equivale ao inverso da modelagem anterior, ou seja,
a chave é representada pela aptidão e o valor é representado pelo indivíduo, isso
permite o agrupamento dos indivíduos pela aptidão, criando subpopulações7
de
indivíduos de alta aptidão, possibilitando que a função reduce utilize os melhores
materiais genéticos (sub-caminho) para gerar novos indivíduos com melhor aptidão.
Essa abordagem foi usada para acelerar a convergência, pois o modelo de Dupla
Geração usa uma só tarefa MapReduce.
5.3 MODELAGEM DO PROBLEMA
O problema do caixeiro viajante tem o objetivo de encontrar o menor
caminho para se percorrer em um conjunto de cidades. A codificação desse caminho
pode ser feita através dos métodos apresentados na seção 4.2.1. Neste trabalho é
usado um PCV Simétrico Euclidiano, como é exemplificado na Figura 5.1 para um
PCVS de dez cidades. Os caminhos são codificados através da representação de
Sequência Ordenada8
, em que as cidades são representadas pela letra do alfabeto
(A, B,..., Z). Para simplificar a demonstração da solução, optou-se por empregar uma
7
Deve-se notar que nem todas as subpopulações criadas são de alta aptidão.
8
Essa codificação é usada por ser mais simples e adequada para os arquivos de texto de entrada e saída usados
no Hadoop.

55
cadeia de cidades (letras) que represente um passeio circular completo, sem
repetição de visitas entre trechos, como é explicado a seguir.
Figura 5.1: Mapa das cidades do PCVS no plano euclidiano.
Para resolver o problema é necessário conhecer as distâncias entre todas as
cidades. Considerando que as cidades são ponto no plano euclidiano, como visto na
Figura 5.1, o processo para encontrar a distância euclidiana entre as cidades é
realizado pelo uso das coordenadas dessas cidades com a equação (1).
(1)
Onde: .
A título de exemplo, adotou-se os valores de coordenadas relativas para
cálculo das distâncias entre as cidades, como visto na Tabela 5.2. Para esse
problema, os caminhos podem ser representados pela sequência das dez primeiras
letras do alfabeto, como a sequência “ABCDEFGHIJ”.
1 2 3 4 5 6 7 8 9 10 11 x
y
11
10
9
8
7
6
5
4
3
2
1
0
A
B
C
D
E
F
G
H
I
J

56
Tabela 5.2: Coordenadas relativas das cidades no plano euclidiano.
Cidade x y
A 1 2
B 7 9
C 3 3
D 1 5
E 4 3
F 5 6
G 2 4
H 8 3
I 9 2
J 6 9
Dessa forma, pode-se calcular a distância percorrida em um caminho, por
exemplo, no cálculo do caminho “ABCDEFGHIJ” da Figura 5.2.
Figura 5.2: Exemplo do cálculo da distância entre as cidades.
5.3.1 Modelagem do Algoritmo Genético
Normalmente, os Algoritmos Genéticos necessitam lidar com grandes
quantidades de indivíduos, pois grandes populações aceleram a convergência para
A
B
C
D
E H
I
J
F
G
Caminho: ABCDEFGIJ = )
Sendo as coordenadas e então:
.
Sendo esse cálculo válido para todo então:
) =
Caminho: ABCDEFGIJ
Distância:

57
uma ótima solução. Isso requer o uso de técnicas para o processamento dessa
grande quantidade de dados, fato que justifica a adoção da técnica MapReduce.
O algoritmo básico para ser aplicado no MapReduce pode ser resumido da
seguinte forma. Antes de começar o processo do AG, é criada uma população com
indivíduos aleatórios; em seguida, são calculadas as aptidões dos novos indivíduos.
Dando início ao processo AG, as iterações criam varias gerações; em cada geração
são selecionados os melhores indivíduos que são utilizados pelos métodos de
cruzamento e de mutação. Para gerar uma nova população, esses novos indivíduos
são submetidos a um novo cálculo de aptidão, em seguida, verifica-se se o AG
atingiu um determinado número de gerações para poder finalizar. Tais
procedimentos são detalhados a seguir.
Inicialmente, é usada uma função aleatória para gerar populações com
grande diversidade. Existem várias alternativas para essa função, como apresentado
na seção 4.1.2. Neste trabalho é usada a Inicialização Randômica Uniforme.
Cada indivíduo da população é avaliado para determinar o valor de sua
aptidão - essa avaliação é feita de acordo com seção 4.2.2. O valor de aptidão é
usado por vários métodos que efetuam a seleção, como os que são apresentados
na seção 4.1.3. Este trabalho usa a seleção por Ranking, e a atualização é feita
através da troca de toda a população.
Após o processo de seleção, os indivíduos são escolhidos em pares de
acordo com a sua ordem na população, esses pares são usados pelo operador de
cruzamento para criar novos indivíduos. Há vários operadores de cruzamento
especializados para o PCV, que podem ser vistos na seção 4.2.3. O operador OX é
o método de cruzamento mais adequado para representação de Sequência
Ordenada (codificação usada neste trabalho), preservando assim mais as estruturas
ordenadas dos cromossomos pais, promovendo a herança genética aos seus
descendentes.
Após o cruzamento, uma amostra dos indivíduos sofre a operação de
mutação. Alguns operadores de mutação são descritos na seção 4.2.4,
especializados para o PCV; neste trabalho é usado o operador de mutação por
intercâmbio recíproco.

58
Durante o processo de cada geração, o melhor indivíduo é comparado com
o melhor encontrado anteriormente, isso permite que o AG armazene o melhor
indivíduo entre todas as gerações, procedimento que se repete até atingir o número
predefinido de gerações.
5.3.2 Modelagem do MapReduce
Para implementar o AG na técnica MapReduce, deve-se utilizar um modelo
que se adapte à organização dessa técnica. Neste trabalho é usada a modelagem
Dupla Geração para que o AG seja executado em uma única tarefa MapReduce. O
modelo Dupla Geração cria dois tipos de gerações, as gerações locais e as
gerações globais, cada uma executa todo o processo do AG descrito na seção
anterior, além disso, a fase Shuffle e Sort9
funciona como um processo de seleção
global.
As gerações locais são criadas por uma iteração na função map. Com uma
população de entrada o processo AG cria novas gerações de indivíduos, que no final
são enviados junto com o melhor indivíduo encontrado (elitismo global) para a fase
intermediária (Shuffle e Sort).
As gerações globais são criadas por uma iteração na função reduce, que
recebe da fase intermediária um conjunto de indivíduos que forma a população
inicial para o processo AG criar novas gerações. No final, o melhor individuo
encontrado é enviado para a saída da função.
O resumo de todo o processo é melhor visto na Figura 5.3. A população de
entrada é gerada randomicamente fora da tarefa MapReduce. Essa população é
dividida entre as tarefas map. Cada divisão forma uma subpopulação local, que é
processada pela função map através do processo AG. Dependendo do tamanho
dessa subpopulação, ela pode ser dividida em grupos menores, que são usadas
como entrada para novos processos AG. A saída da função tem como chave a
aptidão e o como valor um indivíduo, que é representado por um cromossomo
9
É a fase intermediária em que o framework MapReduce executa a classificação (Sort) e a transferência de
dados da fase map para a fase reduce, que é conhecida como o Shuffle (embaralhamento).

59
(caminho) e sua aptidão (a distância do caminho). A função reduce recebe uma
subpopulação formada por indivíduos de aptidão aproximada que é usada por um só
processo AG, enviando um só indivíduo no final de cada função reduce.
Figura 5.3: Funcionamento do processamento MapReduce para o Algoritmo
Genético no modelo Dupla Geração.
O poder do processamento paralelo permite dividir a população em várias
tarefas map, que corresponde à execução paralela de vários processos AG sobre
uma subpopulação. Na fase reduce podem ser criadas varias tarefas reduce, que
proporciona a execução paralela de vários processos AG, em que cada tarefa
reduce executa um só processo AG.
Sob a perspectiva da visão de fluxo de dados, o funcionamento do AG na
técnica MapReduce é descrito da seguinte forma, considerando a codificação de
cidades (em forma de letras) adotado neste capítulo.
Inicialmente os dados utilizados são provenientes de um arquivo texto, em
que cada linha é uma representação codificada de um indivíduo, como por exemplo:
ABCDEIGHFJ
GIJABEFCDH
BEFGHIJACD
EBGFHCDIJA
Entrada Map SaídaReduceShuffle
& Sort
População
Randômica
Subpopula
ção Local
AG AGSubpopula
ção Geral
Melhores
Indivíduos

60
Os dados do arquivo de entrada formam pares chave/valor: a chave é o
número da linha (que não é tratado no arquivo), e o valor é própria linha que
representa o indivíduo. A função map avalia e armazena uma quantidade de linhas
(indivíduos) em uma lista, formando a população inicial para o processo AG gerar
novos indivíduos, esses são emitidos na forma do par aptidão/indivíduo
(chave/valor), sendo que a chave é o arredondamento da aptidão para um número
inteiro e o valor é um par <cromossomo/aptidão>10
. No final de cada emissão há um
retorno da coleta de dados de entrada, se ainda houver dados de entrada, o
processo AG da função map se repete, emitindo novos pares aptidão/indivíduo como
no exemplo:
( 53, <ABCDEFGHIJ, 53.3475288096413>)
( 51, <GHIJABEFCD, 50,6532924781218>)
( 53, <EBFHGIJACD, 52.8074130652778>)
( 51, <EBHFCDIJGA, 51.4288322764095>)
A saída da função map é processada pela fase intermediária (Shuffle e Sort),
agrupando os pares aptidão/indivíduo (chave/valor) pela aptidão, porém essa forma
gera o risco de executar várias funções reduce com um só indivíduo, tornando inútil
o processo AG; isso é evitado se a chave do par aptidão/indivíduo for uma
aproximação da aptidão. Após a fase intermediária os dados são enviados para a
fase reduce da seguinte forma:
(51, [<GHIJABEFCD, 50,6532924781218>, <EBHFCDIJGA, 51.4288322764095>])
(53, [<ABCDEFGHIJ, 53.3475288096413>, <EBFHGIJACD, 52.8074130652778>])
Para cada chave há uma lista de indivíduos, que é usada pela função reduce
para gerar uma nova população através do processo AG. Na função reduce a chave
não é utilizada e a lista é usada como população inicial. No final da tarefa é emitido o
melhor indivíduo de cada função reduce através do par aptidão/indivíduo, como
desta forma:
(27.866056254812328, ACEHIBJFDG)
(28.014106081769356, GFJBHIECAD)
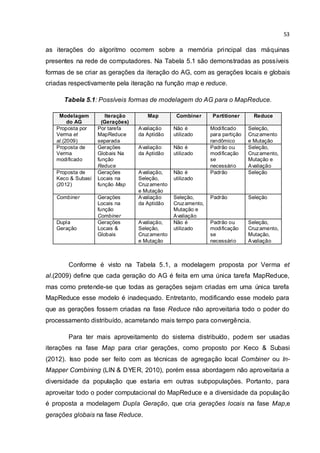
Todo esse processo de fluxo de dados pode ser visto na Figura 5.4.
10
Na modelagem MapReduce o par <cromossomo/aptidão> e o cromossomo (caminho) tem a mesma
denominação “Indivíduo”.

61
Figura 5.4: Fluxo lógico de dados do processo MapReduce para o AG.
Na essência do processo, as funções map e reduce mantém o controle dos
melhores indivíduos, no qual são sempre enviados pelo fluxo de dados. Isso resulta
na saída dos melhores indivíduos encontrados para o PCV. No término do processo
é realizada a gravação das saídas da fase reduce em um arquivo no sistema de
arquivos do Hadoop (o HDFS).
5.4 IMPLEMENTAÇÃO
Com base na estrutura de funcionamento do algoritmo genético PCV, esta
seção apresenta a implementação da aplicação denominado PCV-AG, no contexto
da tecnologia MapReduce do Hadoop. Para facilitar o entendimento da solução, as
funções principais de mapeamento e redução estão codificadas em forma de
algoritmos; as listagens em código Java encontram-se na seção de anexos.
5.4.1 Algoritmo
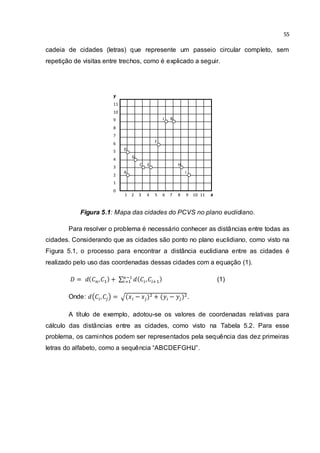
A função map é implementada pela classe MAPPER, descrito no algoritmo
da Figura 5.5. Nessa classe há três métodos:
1) MAP: trata e processa os valores de entrada para criar novos indivíduos,
inserindo cada um em uma nova população (grupo da subpopulação), que tem o
tamanho gerenciado por um controle de balanceamento, esse controle chama o
método GERACAOLOCAL quando a população atingir um determinado tamanho.
Entrada | map |
| shuffle
reduce > Saída
ABCDEIGHFJ
GIJABEFCDH
BEFGHIJACD
EBGFHCDIJA
( 0, ABCDEIGHFJ)
( 1, GIJAB EFCDH)
( 2, BEFGHIJACD)
( 3, EBGFHCDIJA)
( 53, < ABCDEFGHIJ, 53.3475288096413>)
( 51, <GHIJABEFCD, 50,6532924781218>)
( 53, <EBFHGIJACD, 52.8074130652778>)
( 51, <EBHFCDIJGA, 51.4288322764095>)
(51, [<GHIJABEFCD, 50,6532924781218>, <EBHFCDIJGA, 51.4288322764095>])
(53, [<ABCDEFGHIJ, 53.3475288096413>, <EBFHGIJACD, 52.8074130652778>])
(27.866056254812328, ACEHIBJFDG)
(28.014106081769356, GFJBHIECAD)
27.866056254812328, ACEHIBJFDG
28.014106081769356, GFJBHIEC AD

62
2) GERACAOLOCAL: responsável por criar a iteração que executa o
processo AG, para criar uma nova geração de indivíduos que são emitidos para fase
intermediária.
3) CLEANUP: é a última função executada pela classe MAPPER, que
chama o método GERACAOLOCAL para processar os últimos indivíduos que não
passaram pelo controle de balanceamento.
Os métodos MAP e GERACAOLOCAL implementam o Algoritmo Genético e
os métodos CLEANUP e GERACAOLOCAL são os que implementam a técnica In-
Mapper Combining.
O Indivíduo do algoritmo é uma estrutura de dados formada pelos atributos
Cromossomo e Aptidão, instanciado como um objeto (Indivíduo) que irá compor a
lista População. Tal lista (População) fornece os métodos Adicionar, Tamanho e
Limpar, que respectivamente realizam as operações de inserir um novo elemento,
retornar o número de elementos, e excluir todos os elementos da lista.
O objeto OperaçãoGenética é uma instância de uma classe de apoio que
implementa todos os métodos do processo AG (seleção, cruzamento, mutação e
cálculo da aptidão), como podem ser vistos nas linhas 16-19. Além desses há
também dois métodos, TaxaMutação e MelhorIndivíduo, que proveem suporte às
operações principais. A TaxaMutação recebe um valor (taxa) que é usado pelo
método mutação; essa taxa varia entre os algoritmos Map e Reduce, que deve ser,
respectivamente, um valor baixo (BaixaTaxa) e um valor alto (AltaTaxa). O método
MelhorIndivíduo retorna (inserindo na lista) o melhor indivíduo encontrado nas
execuções dos métodos do objeto OperaçãoGenética. A variável
ValorDeBalanceamento define o tamanho da lista População e controla quando
processo AG será executado. As variáveis Geração e CondiçãoDeParada define,
respectivamente, o número da execuções do processo AG e o número máximo de
iteração desse processo.
O algoritmo Map provê dois métodos de apoio, o Arredondar e o Emite. O
Arredondar é usado para transformar o número real do atributo Aptidão do Indivíduo
para um número inteiro; esse valor é armazenado na variável Aptidão. O método

63
Emite permite gerar os dados (a variável Aptidão e o Indivíduo) para fase
intermediária.
1: classe MAPPER
2: atributo População  novo objeto lista [Indivíduo ]
3: atributo OperaçãoGenética  novo objeto OperaçãoGenética
4: método MAP (chave, valor)
5: Indivíduo  novo objeto Indivíduo
6: Indivíduo.Cromossomo  valor
7: Indivíduo.Aptidão  OperaçãoGenética.CalcularAptidão(Indivíduo)
8: População.Adicionar(Indivíduo)
9: OperaçãoGenética.TaxaMutação(BaixaTaxa)
10: se (População.Tamanho() = ValorDeBalanceamento)
11: GeracaoLocal ()
12: método GERACAOLOCAL ()
13: variável CondiçãoDeParada  NúmeroMáximoDeGerações
14: variável Geração  0
15: enquanto (Geração < CondiçãoDeParada)
16: População  OperaçãoGenética.Seleção(População)
17: População  OperaçãoGenética.Cruzamento(População)
18: População  OperaçãoGenética.Mutação(População)
19: População  OperaçãoGenética.CalcularAptidão(População)
20: Geração  Geração + 1
21: fimEnquanto
22: População.Adicionar(OperaçãoGenética.MelhorIndivíduo())
23: para todo Indivíduo em População faça
24: variável Aptidão  Arredondar(Indivíduo. Aptidão)
25: Emite (Chave Aptidão, Valor Indivíduo)
26: fimParaTodo
27: População.Limpar()
28: método CLEANUP ()
29: GeraçãoLocal ()
Figura 5.5: Código Map do Algoritmo Genético MapReduce.
A função reduce é implementada pela classe REDUCER, descrita no
algoritmo da Figura 5.6. Essa classe tem o método REDUCE, responsável por criar a
iteração que executa o processo AG, que manipula uma subpopulação de indivíduos
de entrada, que é processada para gerar novos indivíduos. No final, o melhor
indivíduo encontrado na subpopulação é emitido para a saída da função.

64
1: classe REDUCER
2: atributo População  novo objeto lista [Indivíduo ]
3: atributo OperaçãoGenética
4: método REDUCE (Chave Aptidão, Valor [Indivíduo ] )
5: População  Valor
6: OperaçãoGenética  novo objeto OperaçãoGenética
7: OperaçãoGenética.TaxaMutação(AltaTaxa)
8: variável CondiçãoDeParada  NúmeroMáximoDeGerações
9: variável Geração  0
10: enquanto (Geração < CondiçãoDeParada)
11: População  OperaçãoGenética.Seleção(População)
12: População  OperaçãoGenética.Cruzamento(População)
13: População  OperaçãoGenética.Mutação(População)
14: População  OperaçãoGenética.CalcularAptidão(População)
15: Geração  Geração + 1
16: fimEnquanto
17: Indivíduo  OperaçãoGenética.MelhorIndivíduo()
18: variável Cromossomo  Indivíduo.Cromossomo
19: variável Aptidão  Indivíduo.Aptidão
20: Emite (Chave Aptidão, Valor Cromossomo)
21: População.Limpar()
Figura 5.6: Código Reduce do Algoritmo Genético MapReduce.
A técnica MapReduce define que os dados do fluxo de dados podem ser de
qualquer tipo. Isso permite que os indivíduos (presentes no fluxo de dados) do
modelo Dupla Geração, sejam definidos como um par cromossomo/aptidão. Dessa
forma, os indivíduos podem ser definidos por uma classe em uma instância que é
vista na linha 5 do algoritmo da Figura 5.5. Tais objetos (indivíduos) são os principais
dados da tarefa MapReduce para a aplicação PCV-AG.
As operações do Algoritmo Genético estão fracamente acoplados ao
algoritmo do MapReduce, isso permite abstraí-los da implementação apresentada na
tecnologia MapReduce, concentrando-os separadamente em uma só classe
denominada “OperaçãoGenética”, como pode-se observar na linhas 16-19 da Figura
5.5, e 11-14 da Figura 5.6, especificamente onde ocorre o processo AG. Assim,
torna o algoritmo Map e Reduce mais simples e flexível para ser adaptado a outros
contextos de problema que sigam o paradigma do Caixeiro Viajante.

65
5.4.2 Implementação em Java
Com base no diagrama de classes da Figura 5.7, e dos algoritmos
apresentados na seção anterior, a aplicação PCV-AG pode é codificada na
linguagem Java (linguagem nativa do Hadoop), cuja listagem completa está
localizada na seção de Anexos. A seguir, trechos dos códigos na implementação
são destacados para explicar as características particulares na tecnologia Hadoop.
Figura 5.7: Diagrama de classe do PCV-AG para o MapReduce.
A Figura 5.8 apresenta o código simplificado da classe Individuo. A classe
Indivíduo é uma implementação da interface Writable (ver seção 3.3.4) que
armazena dois valores: o cromossomo do indivíduo que é uma cadeia de caractere
(String) e sua aptidão que é um número real (double). Os objetos dessa classe são
usados em todo processamento da aplicação PCV-AG e no fluxo de dados do
MapReduce.

66
Figura 5.8: Código simplificado da classe Indivíduo.
A Figura 5.9 apresenta o código simplificado do CaixeiroViajanteMapper. A
classe CaixeiroViajanteMapper é uma extensão da superclasse Mapper (ver seção
3.3.4), onde é definido os tipos de entradas e de saída. Os tipos da chave e valor de
entrada são respectivamente Object e Text. Os tipos da chave e valor de saída são
respectivamente IntWritable e Indivíduo. A classe possui os atributos população e
operacaoGenetica que são, respectivamente, uma lista de Indivíduo e um objeto do
tipo OperaçãoGenética, que são usados para a criação dos grupos de indivíduos,
para o armazenamento do melhor indivíduo e para fornecer as operações para o
processo AG.
Figura 5.9: Código simplificado da classe CaixeiroViajanteMapper.
A classe CaixeiroViajanteMapper também possui dois métodos herdadas
da classe Mapper, os métodos map() e cleanup(), e um método auxiliar
geraçãoLocal(). O método map() tem três parâmetros, os dois primeiros são
public class CaixeiroViajanteMapper extends Mapper<Object, Text,
IntWritable, Individuo> {
private ArrayList<Individuo> populacao = new ArrayList<Individuo>();
private OperacaoGenetica operacaoGenetica = new OperacaoGenetica();
@Override
public void map(Object key, Text value, Context context)
throws IOException, InterruptedException {…}
public void geracaoLocal(Context context) throws IOException,
InterruptedException {…}
@Override
protected void cleanup(Context context) throws IOException,
InterruptedException {…}
}
public class Individuo implements Writable {
private String cromossomo;
private double aptidao;
@Override
public void write(DataOutput out) throws IOException {…}
@Override
public void readFields(DataInput in) throws IOException {…}
}

67
corespondentes ao par chave/valor de entrada e o último ao objeto Context11
. O
método geraçãoLocal() recebe como argumento o objeto Context, usado para a
emissão dos indivíduos para a fase intermediária.
Na Figura 5.10 é visto o código simplificado do CaixeiroViajanteReducer. A
classe CaixeiroViajanteReducer é uma extensão da superclasse Reducer (ver
seção 3.3.4), onde é definido os tipos de entradas e de saída. Os tipos da chave e
valor de entrada são, respectivamente, IntWritable e Indivíduo. Os tipos da chave e
valor da saída são, respectivamente, DoubleWritable e Text. A classe possui os
mesmos atributos da classe CaixeiroViajanteMapper para a mesma finalidade.
Figura 5.10: Código simplificado da classe CaixeiroViajanteReducer.
A classe CaixeiroViajanteReducer herda da superclasse Reducer o método
reduce(), no qual tem três parâmetros, os dois primeiro são correspondentes ao par
chave/valor de entrada, e o último ao objeto Context. O método cria as gerações
através do mesmo processo AG através do atributo operacaoGenetica, empregando
o objeto Context para a emissão do melhor indivíduo encontrado.
Na Figura 5.11 é apresentado o código simplificado da classe
OperacaoGenetica. A classe OperaçãoGenética é uma classe auxiliar que executa
todas as funcionalidades das operações do AG. Os principais atributos são
melhorIndivíduo, alfabeto, distâncias e taxaMutação. O atributo melhorIndivíduo tem
o objetivo de guardar o melhor indivíduo encontrado durante o processo AG. Os
atributos alfabeto e distâncias armazenam as principais informações das cidades. O
atributo taxaMutação define a porcentagem de mutação da população. A classe
11
Objeto que permite que aplicação se comunique e envie dados para o framework do Hadoop.
public class CaixeiroViajanteReducer extends Reducer<IntWritable,
Individuo, DoubleWritable, Text> {
private OperacaoGenetica operacaoGenetica;
@Override
public void reduce(IntWritable key, Iterable<Individuo> values,
Context context) throws IOException, InterruptedException {…}
}

68
OperaçãoGenética tem os métodos principais, calcularAptidão(), seleção(),
cruzamento(), mutação() e os auxiliares setTaxaMutação() e getMelhorIndivíduo().
Figura 5.11: Código simplificado da classe OperacaoGenetica.
Os métodos calcularAptidão, seleção, cruzamento e mutação, recebem uma
população de indivíduos para efetuar sua operação genética, e no final retornam a
população processada. O método setTaxaMutação() define a porcentagem usada
pelo método mutação(); essa taxa é diferente para as funções map e reduce. O
método getMelhorIndivíduo() retorna o melhor indivíduo armazenado no atributo
melhorIndivíduo.
Finalmente, a classe CaixeiroViajante é a classe que executa o trabalho
MapReduce. Para isso, a partir do método estático main(), há o controle da
execução do trabalho, a definição da entrada e saída do caminho do arquivo ou
diretório dos dados, a especificação de quais classes fazem parte da função map e
reduce, e o controle dos tipos de entrada e saída das funções map e reduce. No
final, o método monitora o progresso do trabalho MapReduce.
public class OperacaoGenetica {
private Individuo melhorIndividuo = new Individuo();
private int tamanhoIndividuo = 10;
private double taxaMutacao = 5/100;
private String alfabeto = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
private int[][] distancias = {{ 1, 2 }, { 7, 9 }, { 3, 3 }, { 1, 5 }, {
4, 3 }, { 5, 6 }, { 2, 4 }, { 8, 3 }, { 9, 2 }, { 6, 9 }};
public ArrayList<Individuo> calcularAptidao(ArrayList<Individuo>
populacao)
public ArrayList<Individuo> selecao( ArrayList<Individuo> populacao)
public ArrayList<Individuo> cruzamento(ArrayList<Individuo> populacao)
public ArrayList<Individuo> mutacao(ArrayList<Individuo> populacao)
public Individuo getMelhorIndividuo()
public void setTaxaMutacao(double taxa)
}

69
5.5 TESTES E AVALIAÇÃO DE RESULTADOS
Para testar o algoritmo da aplicação PCV-AG foi usado um PCVS de vinte
cidades, com base no desempenho do algoritmo, para encontrar as melhores
soluções em função do número de indivíduos da população inicial. A aplicação é
executada em um só computador, no modo local (standalone mode) do Hadoop, que
é o mais indicado para o desenvolvimento da aplicação AG MapReduce, porém não
fornece todo o poder de processamento paralelo presente no modo distribuído em
uma rede de computadores. Portanto, as análises estão focadas apenas no
potencial da modelagem MapReduce, e não no poder de processamento paralelo,
que é apenas simulado no modo local.
5.5.1 Ambiente operacional e cenário de execução
A aplicação PCV-AG é implementado em Java e utiliza a API do Hadoop
1.2.1, Java 1.7, e a IDE12
Eclipse JEE Enterprise (Juno) com o hadoop-eclipse-
plugin 1.2.
A execução foi realizada em modo local (standalone mode) em uma
máquina de 1,67 GHz de processamento, com 1GB de memória principal. O sistema
operacional é o Ubuntu (versão 12.04.3), simulando o ambiente Hadoop no Eclipse,
com o uso do plugin hadoop-eclipse-plugin 1.2.
O PCVS usado para os testes tem a mesma descrição do exemplo anterior,
porém o número de cidades e as coordenadas são diferentes. Esse novo cenário
apresenta 20 (vinte) cidades, cujo espaço de busca é maior que 60,822 quatrilhões
de possibilidades de caminhos. As coordenadas cartesianas dessas cidades estão
descritas na Tabela 5.3.
12
Ambiente de Desenvolvimento Integrado.

70
Tabela 5.3: Coordenada das cidades do problema.
Cidade X Y Cidade x y
A 1 8 K 17 10
B 1 10 L 17 8
C 2 13 M 16 5
D 3 15 N 15 3
E 5 16 O 13 2
F 8 17 P 10 1
G 10 17 Q 8 1
H 13 16 R 5 2
I 15 15 S 3 3
J 16 13 T 2 5
As coordenadas das cidades formam uma figura circular de acordo com a
Figura 5.12, escolhida pelo fato de ser possível reconhecer visualmente o melhor
caminho e comparar com os caminhos encontrados pela aplicação. O melhor
indivíduo é representado pela ordem da sequência dos pontos
“ABCDEFGHIJKLMNOPQRST”, com aptidão igual a 51,1867651013453.
Figura 5.12: Mapa do conjunto de 20 cidades no plano euclidiano.
As funções map e reduce da aplicação PCV-AG possuem em cada
processo AG uma iteração de 10 (dez) gerações. Na função map, a taxa de
mutação é definida em 5% da população, e o balanceamento em 100 (cem)
indivíduos.
Na função reduce a taxa de mutação é de 90%. Essa taxa deve ser alta, pois
cada tarefa reduce recebe indivíduos de aptidão aproximados, aumentando assim a
A
G
C
E
F
I
J
H
B
D
L
K
PQ
M
N
OR
S
T

71
possibilidade de indivíduos semelhantes e, com isso, elevando o risco de
convergência prematura. A população inicial é gerado aleatoriamente, através de
uma aplicação MapReduce.
5.5.2 Simulações e resultados obtidos
No trabalho de Huang & Lin (2010) é demonstrada uma implementação de
um AG MapReduce para resolver o problema Job Shop Scheduling Problem, com o
objetivo de demonstrar o impacto do tamanho da população no resultado e no tempo
de convergência. O resultado obtido no trabalho demonstra que quanto maior a
escala da população, não só tendem a encontrar melhores soluções, mas também
exige menos gerações. O teste realizado aqui, demonstra o mesmo resultado,
porém não é avaliado o tempo de convergência por estar sendo usada uma só
maquina. Outro item que não é avaliado é o número de geração, pois esse número é
um valor predefinido no algoritmo do MapReduce, que impossibilita a análise do
desempenho do algoritmo baseado no número de geração.
O teste foi realizado sobre 5 (cinco) escalas de população, de acordo com a
Tabela 5.4, em que cada escala foi gerada 4 (quatro) populações de indivíduos
aleatórios, que por sua vez são realizadas cinco execuções da aplicação PCV-AG,
resultando na saída de várias dezenas de indivíduos, na faixa de 80 a 150, na qual
só foi selecionado o melhor.
Em cada escala houve 20 execuções, resultando em 20 melhores
indivíduos. Desses, foi retirado o melhor, o pior e uma média. Para comparação, foi
retirado de cada população inicial a aptidão dos melhores, e definido o melhor, o pior
e a média das melhores aptidões por escala.

72
Tabela 5.4: Aptidão das Populações Iniciais e das Populações Finais resultante das
execuções do PCV-AG.
Escala População Inicial População Final
Melhor
Inicial
Pior
Inicial
Média
Inicial
Melhor
Gerado
Pior
Gerado
Média
Gerada
1000 124,0074 151,8577 132,2208 80,59109 110,0509 98,69151
10000 123,6807 148,7945 136,6492 69,36951 94,82906 84,77589
20000 120,0181 139,7515 131,6790 71,57708 93,43644 82,72006
30000 129,9764 134,2425 131,9972 59,28971 88,4677 77,65220
40000 130,0537 136,1151 132,2208 65,53783 83,86628 75,50903
Os resultados obtidos são comprovados no gráfico da Figura 5.13,
enfatizando que o aumento no número de indivíduos da população, demonstra que a
aplicação gera indivíduos próximos da melhor solução. Esta afirmação pode ser
observada pela linha da média gerada, e também pela tendência das linhas do
melhor e pior individuo gerado. A média dos melhores indivíduos iniciais tende a
permanecer constante, reforçando que a convergência dos indivíduos gerados se
deve ao número de indivíduos da população inicial.
Figura 5.13: Tendência gerada pelo aumento de escala da população.
O melhor e pior indivíduo encontrados podem ser vistos graficamente na
Figura 5.14. O melhor indivíduo é o caminho representado pela sequência
0
20
40
60
80
100
120
140
160
0 10000 20000 30000 40000 50000
Aptidão(Tamanhodocaminho)
Número de indivíduo da população
PIORINICIAL
MÉDIA INICIAL
MELHOR INICIAL
PIORGERADO
MÉDIA GERADA
MELHOR GERADO
MELHOR CAMINHO

73
“ONMKLJHIGFEDCBATSRQP” de aptidão 59.289708664779766, e o pior indivíduo
é o caminho “JIHSCFEDBARTQPONKLMG”, de aptidão 110.05093343072689.
Figura 5.14: Melhor e pior indivíduo encontrado entre os melhores.
Por não estar sendo executado no modo distribuído, o tempo de execução
da aplicação foi de 5 a 49 segundos, dependendo do tamanho da escala da
população.
5.5.3 Desempenho da Modelagem Dupla Geração
Na modelagem Dupla Geração, para a criação das iterações na fase map é
utilizada a técnica in-mapper combining, cujo efeito colateral danoso é provocar um
gargalo de escalabilidade, um problema para o modelo que pretende escalar e
trabalhar com grande população. A solução é utilizar um controle de balanceamento
para processar um número predefinido de indivíduos. Entretanto, nesse tipo de
abordagem o número de indivíduos dessas subpopulações deve ser definido
empiricamente, o que afeta a qualidade da geração local, pois como foi
demonstrado, o tamanho da população inicial afeta o grau de convergência.
A condição de convergência do algoritmo foi determinada com base em um
número predefinido de gerações, situação que pode não encontrar o melhor
indivíduo, mas uma aproximação. Se for utilizada uma condição de convergência
Melhor Indivíduo Pior Indivíduo

74
que dependa do valor da aptidão, uma tarefa map pode levar muito tempo para a
convergência, até travar todo o processo MapReduce, pois a fase Reduce depende
da conclusão da fase anterior, podendo induzir o framework MapReduce a finalizar a
tarefa pela sua lentidão. A consequência da abordagem adotada é que a aplicação
pode não gerar o melhor individuo, e sim um indivíduo de alta aptidão, como pode
ser visto no gráfico da Figura 5.13, tendo como fator de convergência mais
significativo o tamanho da escala da população.
Na modelagem do fluxo de dados, o par chave/valor de saída da função map
é definido pelo par aptidão/indivíduo, dessa forma, durante a fase intermediária os
indivíduos de diferentes populações são agrupados por aptidão aproximada, no qual
são usados pela função reduce, criando novas gerações. Essa abordagem foi usada
para acelerar a convergência, mas surge a dificuldade com o aumento da
possibilidade de cruzamento de indivíduos semelhantes, elevando o risco de
convergência prematura, ficando presa no ótimo local. Para resolver esse problema,
foi definido no algoritmo genético, na fase Reduce, uma alta taxa de mutação,
suficiente para sair do ótimo local. Apesar disso, independente da taxa de mutação,
a função reduce tende a gerar melhores indivíduos em relação à entrada, causada
pela diversidade da população das tarefas map.
5.6 CONSIDERAÇÕES FINAIS
Este capítulo apresentou a modelagem de Algoritmo Genético na técnica
MapReduce, para resolver o Problema do Caixeiro Viajante. Foi proposta uma
modelagem e implementação para a execução simples do AG em uma única tarefa
MapReduce.
O AG é uma técnica de otimização usada para encontrar solução de um
problema, como no caso do Problema do Caixeiro Viajante. O MapReduce fornece a
escalabilidade de dados e o processamento necessário para o AG, potencializando
a capacidade de encontrar um bom resultado em um espaço de busca
extremamente grande.

75
Os Algoritmos Genéticos possuem características que não permitem ser
exatamente expressa no modelo MapReduce. Para resolver esse problema, foi
desenvolvido formas diferentes de modelar o AG.
A modelagem do AG desse trabalho usa as melhores características
apresentadas por outros modelos, criando um novo modelo que aproveita os
recursos da diversidade da população, do processamento e do tempo de execução.
É possível usar outras formas de modelagem, como o uso do Combiner para criar
novas iterações, e do Partitioner para criar novas formas de seleção global para a
fase Reduce.
A medição do tempo de convergência da aplicação não foi avaliada pelo fato
da aplicação está sendo executada no modo local. Para fazer essa avaliação seria
necessário executar em modo distribuído do Hadoop em um cluster de máquinas
organizados em uma rede de computadores.
Considerando as limitações do ambiente operacional (modo local), foi
escolhido um cenário mais simples, com um exemplo considerado pequeno de
cidades, ainda assim produzindo um bom espaço de busca para as análises dos
resultados.
O controle de balanceamento possui um valor que define o tamanho das
subpopulações da tarefa map. Nos testes realizados foi definido um baixo valor, mas
dependendo do problema pode aumentar até a capacidade dos recursos
computacionais que o Hadoop e a máquina podem fornecer. Tais recursos são
demandados a partir da definição do número de divisões da população inicial, que
provoca a criação de várias subpopulações e, consequentemente, na criação de
vários processos AG. Quando maior o número do valor de balanceamento menor
será o número de processos AG, que, por sua vez, maior será o tamanho da
subpopulação. O resultado desse ajuste, pode melhorar a qualidade dos indivíduos
nas gerações, mas também necessitará de mais recurso computacional, podendo
atingir o limite dos recursos disponíveis para uma única tarefa map.
A aplicação usa a técnica MapReduce para processar grande volume de
indivíduos, dessa forma a avaliação da aplicação é baseada nos resultados
encontrados em função do tamanho da população inicial. O número de gerações foi

76
definido baixo para que a diversidade da população se sobressaia e seja verificado o
impacto da população inicial, mas o número de gerações pode ser maior,
dependendo da necessidade do problema a ser usado. O resultado encontrado na
simulação da aplicação não diz o tamanho da população necessário para encontrar
uma solução próxima do ideal, e sim que ela deve ser um volume grande de
indivíduos, fato que justifica a utilização do MapReduce para escalar esse grande
volume.
A condição de parada do processo AG por número de gerações é utilizado
para evitar que o framework MapReduce interrompa a execução das tarefas map da
aplicação. No entanto, o processo AG pode utilizar outra condição de parada, como
a por grau de convergência da população, modelando em uma forma adequada em
que todas as tarefas não sejam interrompidas na execução.
A saída da função map é processada pela fase intermediária. Os dados são
agrupados pela aptidão, porém essa forma pode gerar população unitária (de único
indivíduo) para a função reduce. A possível solução para esse problema é definir
uma chave intermediária que seja uma aproximação da aptidão. A forma adotada
neste trabalho foi um arredondamento da chave intermediária para um número
inteiro, no entanto isso pode não ser o suficiente. Neste caso, a melhor alternativa é
o calcular o arredondamento da chave para a dezena ou centena mais próxima.
Assim, o método de arredondamento a ser adotado depende somente da dispersão
dos valores das aptidões. O impacto na qualidade das gerações que o
arredondamento tem no Reduce é semelhante ao controle de balanceamento tem no
Map, pois ambos são responsáveis por delimitar a população inicial para os
processos AGs.
A modelagem proposta não foi comparada com outros modelos para verificar
sua vantagem e desvantagem. Para verificar se o modelo sana os problemas
apresentados por outros modelos, o ambiente de execução (deste trabalho) deveria
executar em modo distribuído, assim seria possível comparar os resultados da
execução da implementação com os outros modelos que aplicam a eficiência dos
ambientes operacionais.

77
O resultado avaliado, foi um modelo para a execução simplificada do AG em
única tarefa MapReduce, aproveitando as característica paralela e distribuída da
técnica MapReduce, bem como a diversidade oferecida por uma grande população.
Dessa forma, o modelo não realiza a distribuição das operações do AG, e sim o
paralelismo de vários processos AG em várias tarefas do MapReduce.

78
CONCLUSÃO
A técnica MapReduce é um modelo de programação utilizado para o
processamento de grandes conjuntos de dados, baseado no ambiente
computacional paralelo e distribuído, que provê escalabilidade e simplificação para o
desenvolvimento de aplicações com essas características. Alguns frameworks
MapReduce estão disponíveis no mercado de software, entre eles o Hadoop, que é
utilizado para o processamento e armazenamento de dados em larga escala,
organizados em clusters de computadores de máquinas comuns. Os recursos e
vantagem que a técnica MapReduce proporciona, torna essa tecnologia adequada
para ser aplicada em vários campos, como o tratamento e análise de agrupamentos
de dados, aprendizado de máquina, visão computacional, entre outros, como é caso
dos Algoritmos Genéticos.
Algoritmo Genético é uma técnica de otimização utilizada como busca
global, empregada em problemas nas quais o número de soluções possíveis para
sua resolução é muito alto. Dessa forma, os recursos computacionais tradicionais
tornam-se inviáveis para resolvê-lo em tempo hábil. Exemplo disso, é o caso do
Problema do Caixeiro Viajante (PCV), no qual o número de combinações de
caminhos para percorrer um conjunto de cidades aumenta exponencialmente em
função do número de cidades. PCV é um problema típico de otimização que é
bastante utilizado em pesquisas e aplicações de diferentes áreas.
Um dos desafios presentes em AG é a necessidade de ter uma grande
quantidade de indivíduos para encontrar uma boa solução, exigindo poder e
escalabilidade dos recursos computacionais. Os AGs possuem algumas
características de natureza paralela, fato que permite ser processado em um arranjo
computacional em uma rede, ou cluster de computadores. Porém, isso requer uma
preparação de rotinas adicionais para a paralelização e distribuição dos processos
AG, dificultando a programação da solução. Para resolver esse problema, uma
alternativa viável é a adoção da técnica MapReduce, que simplifica o algoritmo de
implementação, permitindo processar grande quantidade de indivíduos e reduzindo
o tempo de execução na busca de um bom resultado. Porém, modelar um AG em

79
MapReduce não é trivial, exigindo a criação de estratégias para o uso eficiente das
duas técnicas.
Este trabalho investigou pesquisas acadêmicas que foram desenvolvidas
para modelar AGs usando a técnica MapReduce. A modelagem proposta neste
trabalho foi empregada e adaptadas algumas características apresentadas nos
modelos investigados, resultando em uma proposição de projeto simplificada para o
AG do tipo PCV. Isso foi possível ser realizado em uma única tarefa MapReduce,
aproveitando as qualidades paralela e distribuída da técnica.
Com base no modelo proposto, foi implementado uma aplicação para a
resolução do PCV. Para facilitar o desenvolvimento do software, a aplicação foi
projetada e executada em modo local, em apenas um computador, fato que
influenciou na escolha de exemplos mais simples, com população de indivíduos que
fossem adequadas para o processamento em uma máquina, e para a melhor
compreensão da codificação da solução. O número de gerações foi definido baixo e
a avaliação da aplicação foi baseada nos resultados encontrados em função do
tamanho da população inicial.
O modelo proposto apresenta algumas restrições: apresenta um método
pouco flexível para controle da população, possui um risco elevado de convergência
prematura, além da possibilidade de ocorrer o travamento da execução em
decorrência de uma escolha inadequada do número predefinido de gerações.
Apesar dessas limitações, o resultado demonstra que o modelo proposto é eficiente
na execução de grande quantidade de dados, situação que reforça o uso da técnica
MapReduce. A evidência disso é comprovada quando se estabelece um tamanho
maior da população inicial, fator que eleva a tendência de encontrar indivíduos de
alta aptidão, mas, em contrapartida, exige poder de processamento distribuído e
paralelo, qualidades presentes na solução MapReduce.
Como trabalhos futuros, pretende-se avaliar o modelo proposto na execução
de testes em cluster de computadores para resolver PCV mais complexos; analisar o
desempenho e o tempo médio de execução em um cenário real; comparar o
desempenho da proposta com outras pesquisas disponíveis na literatura; adaptar o

80
modelo para resolver outros problemas de otimização; aplicar as funções Combiner
e Partitioner para melhorar o desempenho do modelo proposto.
Enfatiza-se a contribuição deste trabalho em situações reais enfrentados no
cotidiano, como a identificação de melhores rotas para a logística de distribuição de
cargas, na visitação de turistas em localidades e logradouros em um grande centro
urbano, além de problemas típicos de otimização no planejamento do transporte
público. Outras aplicações encontram-se na área industrial de manufatura de
equipamentos eletrônicos, com a otimização de layout de placas de circuito
impresso, buscando encontrar as melhores configurações.

81
REFERÊNCIAS BIBLIOGRÁFICAS
ALBA, E.; TROYA, J. M. A Survey of Parallel Distributed Genetic Algorithms.
Complexity, v. 4, n. 4, p.31-52, 1999. Disponível em: < http://
http://neo.lcc.uma.es/Articles/albatroyaxx_2.pdf >. Acesso em: 10 jan. 2014, 17:16.
BU, Y.; HOWE, B.; BALAZINSKA, M.; ERNST D. M. HaLoop: Efficient Iterative
Data Processing on Large Clusters. In: Proceeding of the VLDB Endowment, v.3,
n. 1-2, p. 285-296, 2010. Disponível em: <
http://www.ics.uci.edu/~yingyib/papers/HaLoop_camera_ready.pdf>. Acesso em: 07
set. 2014, 21:15.
BRYANT, K.; BENJAMIN, A. Genetic Algorithms and the Traveling Salesman
Problem. In: Proceeding of 1st
GNT Regional Conference on Mathematics, Statistics
and Applications. 2000. Disponível em: < http://... >. Acesso em: 06 fev. 2014,
19:57.
DEAN, J.; GHEMAWAT, S. MapReduce: Simplified Data Processing on Large
Clusters. Communications of the ACM, 51 (1): 107-113, 2008. Disponível em:
<http://www.ccs.neu.edu/home/lieber/courses/csg113/f08/materials/p107-dean.pdf>.
Acesso em: 28 set. 2013, 18:47.
EMC. Disponível em: <http://brazil.emc.com/>. Acesso em: 20 set. 2014, 17:31.
EKANAYAKE, J.; LI, H.; ZHANG, B.; GUNARATHNE, T.; BAE, S.-H.; QIU, J.; FOX,
G.; Twister: A Runtime for Iterative MapReduce. In: HPCA ’10: Proceedings of the
19th ACM International Symposium on High Performance Distributed Computing.
ACM, 2010. p. 810–81.
<http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.212.5045&rep=rep1&type
=pdf>Acesso em: 29 set. 2013, 19:13.
ER, H.; ERDOGAN, N. Parallel Genetic Algorithm to Solve Traveling Salesman
Problem on MapReduce Framework using Hadoop Cluster. arXiv preprint arXiv:
1401.6267, 2014. Disponível em:
<http://arxiv.org/ftp/arxiv/papers/1401/1401.6267.pdf> Acesso em: 25 abr. 2014,
17:47.
GOLDMAN, A.; KON, F.; PEREIRA. F.; POLATO, I.; PEREIRA, R.F. Apache
Hadoop: conceitos teóricos e práticos, evolução e novas possibilidades. XXXI
Jornadas de Atualizações em Informática, 2012. Disponível em: <
http://www.ime.usp.br/~ipolato/JAI2012-Hadoop.pdf>. Acesso em: 29 set. 2013,
17:44.
GUTIN, G. Traveling salesman problem. In: Floudas, C.A., Pardalos, P.M. (eds)
Encyclopedia of Optimization, pp. 3935-3944. Springer, New York, 2009. Disponível
em: <http://eprints.pascal-network.org/archive/00005214/01/TSPentry.pdf >. Acesso
em: 25 abr. 2014, 17:35.
HADOOP. Disponível em: <http://hadoop.apache.org/>. Acesso em: 04 mar. 2014,
12:52.

82
HE, B.; FANG, W.; LUO, Q.; GOVINDARAJU, N.; WANG, T. Mars: A MapReduce
Framework on Graphics Processors. In: PACT ‘08, Proceedings of the 17th
International Conference on Parallel Architectures and Compilation Techniques,
Toronto, Ontario, Canada, 2008. p. 260-269 Disponível em: <
http://www.cse.ust.hk/gpuqp/Mars_tr.pdf>. Acesso em: 11 dez. 2013, 19:05.
HUANG, D.; LIN, J.; Scaling Populations of a Genetic Algorithm for Job Shop
Scheduling Problems using MapReduce. In: Cloud Computing Technology and
Science (CloudCom), 2010 IEEE Second International Conference on. Washington
DC, IEEE, 2010. p. 780-785. Disponível em: < http://hcil2.cs.umd.edu/trs/2010-
14/2010-14.pdf >. Acesso em: 10 jan. 2014, 17:23.
JIN, C.; VECCHIOLA, C.; BUYYA, R. MRPGA: An Extension of MapReduce for
Parallelizing Genetic Algorithms. In: eScience ’08: Fourth IEEE International
Conference on eScience. Washington DC, EUA, 2008. p. 214-221. Disponível em:
<http://www.buyya.com/papers/MapReduce-GA-eScience2008.pdf>. Acesso em: 29
set. 2013, 19:54.
KRUIJF, M.; SANKARALINGAM, K. MapReduce for the Cell B.E. Architecture.
Technical Report TR1625, Department of Computer Sciences, The University of
Wisconsin-Madison, Madison, 2007, Disponível em: <
http://pages.cs.wisc.edu/~dekruijf/docs/mapreduce-cell.pdf >. Acesso em: 21 dez.
2013, 11:04.
KECO, D.; SUBASI, A. Parallelization of genetic algorithms using Hadoop
Map/Reduce. SouthEast Europe Journal of Sorft Computing, v. 1, n. 2, 2012.
Disponível em: <
http://www.researchgate.net/profile/Abdulhamit_Subasi/publication/258858471_Paral
lelization_of_genetic_algorithms_using_Hadoop_ Map/Reduce >. Acesso em: 09
set. 2014, 23:17.
LIN, J.; DYER, C. Data-Intensive Text Processing with MapReduce. Morgan &
Claypool Publishers, 2010. Disponível em: <http://beowulf.csail.mit.edu/18.337-
2012/MapReduce-book-final.pdf>. Acesso em: 29 set. 2013, 20:02.
LUCAS, Diogo C. Algoritmos Genéticos: uma Introdução. 2002. Disponível em: <
.inf.ufrgs.br alvares INF01048IA ApostilaAlgoritmosGeneticos.pdf >. Acesso
em: 01 set. 2013, 11:33.
MISHRA, A.; Genetic Algorithm for the Travelling Salesman Problem on
Hadoop. New York, Rochester, 2011. Tese de Doutorado. Rochester Institute of
Technology. Disponível em:
<http://www.cs.rit.edu/~axm1820/Project_Report_Final.pdf >. Acesso em: 08 set.
2014, 10:32.
PACHECO, M. Algoritmos Genéticos: Princípios e Aplicações. ICA: Laboratório
de Inteligência Computacional Aplicada. Departamento de Engenharia Elétrica.
Pontifícia Universidade Católica do Rio de Janeiro, 1999. Disponível em:
<http://www2.ica.ele.puc-rio.br/Downloads/38/CE-Apostila-Comp-Evol.pdf>. Acesso
em: 01 set. 2013, 11:36.

83
RANGER, C.; RAGHURAMAN, R.; PENMETSA, A.; BRADSKI , G.; KOZYRAKIS, C.,
Evaluating MapReduce for multi-core and multiprocessor systems. In: HPCA
’07: Proceedings of the 2007 IEEE 13th International Symposium on High
Performance Computer Architecture, 2007, Washington, DC, USA. Anais... IEEE
Computer Society, 2007. p.13–24. Disponível em: <
http://pages.cs.wisc.edu/~david/courses/cs758/Fall2009/papers/mapreduce.pdf>.
Acesso em: 11 dez. 2013, 19:11.
VERMA, A.; LLOR`A, X.; GOLDBERG, D.; CAMPBELL, R. Scaling Genetic
Algorithms using MapReduce. In: Intelligent Systems Design and Applications,
2009, ISDA ’09. Ninth International Conference on. IEEE, 2009. P. 13-18. Disponível
em: < http://www.verma7.com/pdfs/ISDA09_MR_GA.pdf>. Acesso em: 29 set. 2013,
17:26.
VENNER, Jason. Pro Hadoop : Build Scalable, Distribuited Applications in the
Cloud. USA, Apress, 2009. Disponível em: < http:// >. Acesso em: 10 jan. 2014,
17:40.
WHITE, Tom. Hadoop: The Definitive Guide. 2.ed. Sebastopol, O'Reilly Media,
2010. Disponível em: <
http://ce.sysu.edu.cn/hope/UploadFiles/Education/2011/10/201110221516245419.pd
f>. Acesso em: 29 set. 2013, 16:45.
YOO, R.M.; ROMANO, A.; KOZYRAKIS, C., Phoenix Rebirth: Scalable
MapReduce on a Large-Scale Shared-Memory System. In IISWC, 2009. p. 198-
207, Disponível em: <
http://csl.stanford.edu/~christos/publications/2009.scalable_phoenix.iiswc.pdf>.
Acesso em: 11 dez. 2013, 18:56.

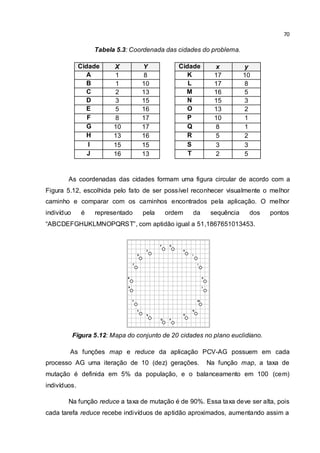
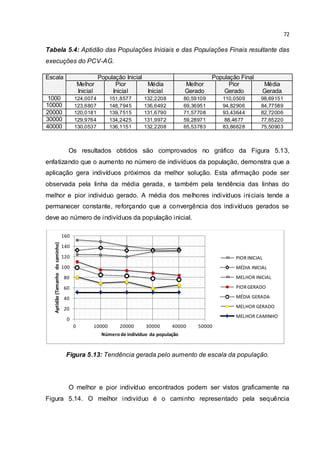
84
ANEXO A
Implementação da classe Individuo.
import java.io.DataInput;
import java.io.DataOutput;
import java.io.IOException;
import org.apache.hadoop.io.Writable;
public class Individuo implements Writable {
private String cromossomo;
private double aptidao;
@Override
public void write(DataOutput out) throws IOException {
out.writeUTF(cromossomo);
out.writeDouble(aptidao);
}
@Override
public void readFields(DataInput in) throws IOException {
this.cromossomo = in.readUTF();
this.aptidao = in.readDouble();
}
@Override
public String toString() {
return cromossomo + "t" + aptidao;
}
public String getCromossomo() {
return this.cromossomo;
}
public void setCromossomo(String individuo) {
this.cromossomo = individuo;
}
public double getAptidao() {
return aptidao;
}
public void setAptidao(double aptidao) {
this.aptidao = aptidao;
}
public String[] getIndArray() {
String[] individuo = new String[this.cromossomo.length()];
for (int i = 0; i < this.cromossomo.length(); i++) {
individuo[i] = ""+this.cromossomo.charAt(i);
}
return individuo;
}
public void setIndArray(String[] individuo) {
this.cromossomo = "";
for (String i: individuo) {
if(i != null){
this.cromossomo += i;
}
}
}
}

85
Implementação da classe CaixeiroViajanteMapper .
import java.util.ArrayList;
import org.apache.hadoop.io.IntWritable;
import org.apache.hadoop.io.Text;
import org.apache.hadoop.mapreduce.Mapper;
public class CaixeiroViajanteMapper extends
Mapper<Object, Text, IntWritable, Individuo> {
private OperacaoGenetica operacaoGenetica = new OperacaoGenetica();
@Override
public void map(Object key, Text value, Context context)
throws IOException, InterruptedException {
ArrayList<Individuo> popula = new ArrayList<Individuo>();
Individuo individuo = new Individuo();
individuo.setCromossomo(value.toString());
popula.add(individuo);
popula = operacaoGenetica.calcularAptidao(popula);
populacao.add(popula.get(0));
operacaoGenetica.setTaxaMutacao(0.05);
if (populacao.size() == 100) {
geracaoLocal(context);
}
}
public void geracaoLocal(Context context) throws IOException,
InterruptedException {
int CondicaoDeParada = 10;
int geracao = 0;
while (CondicaoDeParada != geracao) {
populacao = operacaoGenetica.selecao(populacao);
populacao = operacaoGenetica.cruzamento(populacao);
populacao = operacaoGenetica.mutacao(populacao);
populacao = operacaoGenetica.calcularAptidao(populacao);
geracao++;
}
populacao.add(operacaoGenetica.getMelhorIndividuo());
int Aptidao;
for (Individuo individuo : populacao) {
Aptidao = (int) Math.round(individuo.getAptidao());
context.write(new IntWritable(Aptidao), individuo);
}
populacao.clear();
}
@Override
protected void cleanup(Context context) throws IOException,
InterruptedException {
geracaoLocal(context);
}
}

86
Implementação da classe CaixeiroViajanteReducer .
import org.apache.hadoop.io.DoubleWritable;
import org.apache.hadoop.mapreduce.Reducer;
public class CaixeiroViajanteReducer extends
Reducer<IntWritable, Individuo, DoubleWritable, Text> {
private OperacaoGenetica operacaoGenetica;
@Override
public void reduce(IntWritable key, Iterable<Individuo> values,
Context context) throws IOException, InterruptedException {
operacaoGenetica = new OperacaoGenetica();
operacaoGenetica.setTaxaMutacao(0.9);
for (Individuo val : values) {populacao.add(val); }
if(populacao.size() == 1) {
operacaoGenetica.setMelhorIndividuo(populacao.get(0));
}
int CondicaoDeParada = 10;
int geracao = 0;
while (geracao < CondicaoDeParada) {
populacao = operacaoGenetica.selecao(populacao);
populacao = operacaoGenetica.cruzamento(populacao);
populacao = operacaoGenetica.mutacao(populacao);
populacao = operacaoGenetica.calcularAptidao(populacao);
geracao++;
}
Individuo ind = operacaoGenetica.getMelhorIndividuo();
context.write(new DoubleWritable(ind.getAptidao()), new
Text(ind.getCromossomo()));
populacao.clear();
}
}
Implementação da classe CaixeiroViajante .
import org.apache.hadoop.fs.Path;
import org.apache.hadoop.io.DoubleWritable;
import org.apache.hadoop.mapreduce.Job;
import org.apache.hadoop.mapreduce.lib.input.FileInputFormat;
import org.apache.hadoop.mapreduce.lib.output.FileOutputFormat;
public class CaixeiroViajante {
public static void main(String[] args) throws Exception {
if (args.length != 2) {
args = new String[2];
args[0] = System.getProperty("user.dir") + "/Input";
args[1] = System.getProperty("user.dir") + "/Output";
}
Job job = new Job();
job.setJarByClass(CaixeiroViajante.class);
job.setJobName("Problema do Caixeiro Viajante");

87
FileInputFormat.addInputPath(job, new Path(args[0]));
FileOutputFormat.setOutputPath(job, new Path(args[1]));
job.setMapperClass(CaixeiroViajanteMapper.class);
job.setReducerClass(CaixeiroViajanteReducer.class);
job.setMapOutputKeyClass(IntWritable.class);
job.setMapOutputValueClass(Individuo.class);
job.setOutputKeyClass(DoubleWritable.class);
job.setOutputValueClass(Text.class);
System.exit(job.waitForCompletion(true) ? 0 : 1);
}
}
Implementação da classe OperacaoGenetica.
import java.util.Random;
public class OperacaoGenetica {
private Individuo melhorIndividuo = new Individuo();
private int tamanhoIndividuo = 20;
private double taxaMutacao = 5/100;
private String alfabeto = "ABCDEFGHIJKLMNOPQRSTUVWXYZ";
private int[][] distancias = {
{ 1, 8 }, { 1,10 }, { 2,13 }, { 3,15 }, { 5,16 },
{ 8,17 }, { 10,17}, { 13,16}, { 15,15}, { 16,13},
{ 17,10}, { 17,8 }, { 16,5 }, { 15,3 }, { 13,2 },
{ 10,1 }, { 8, 1 }, { 5, 2 }, { 3, 3 }, { 2, 5 } };
public ArrayList<Individuo> calcularAptidao(ArrayList<Individuo> populacao)
throws IOException {
ArrayList<Individuo> popula = new ArrayList<Individuo>();
double aptidao =0;
int x1, x2, y1, y2, pos;
String[] indString;
for (Individuo indi : populacao) {
indString = new String[tamanhoIndividuo];
indString = indi.getIndArray();
for (int j = 0; j < tamanhoIndividuo; j++) {
pos = alfabeto.indexOf(indString[j]);
x1 = distancias[pos][0];
y1 = distancias[pos][1];
pos=alfabeto.indexOf(indString[(j+1)%tamanhoIndividuo]);
x2 = distancias[pos][0];
y2 = distancias[pos][1];
aptidao+=Math.sqrt(Math.pow(x1-x2,2)+Math.pow(y1-y2,2));
}
indi.setAptidao(aptidao);
setMelhorIndividuo(indi);
popula.add(indi);
aptidao = 0;
}
return popula;
}
public ArrayList<Individuo> selecao( ArrayList<Individuo> populacao) throws
IOException {
int tamanhoPop = populacao.size();
Individuo[] popula = new Individuo[tamanhoPop];
popula = populacao.toArray(popula);

88
popula = QuickSort(popula, 0, tamanhoPop - 1);
populacao.clear();
for(int i=0;i<(popula.length*(1-0.3));i++){populacao.add(popula[i]);}
for(int i=0; i<(popula.length*0.3); i++){populacao.add(popula[i]);}
return populacao;
}
private Individuo[] QuickSort(Individuo[] pop, int inicio, int fim) {
int meio;
if (inicio < fim) {
int topo, indice;
Individuo pivo;
pivo = pop[inicio];
topo = inicio;
for (indice = inicio + 1; indice <= fim; indice++) {
if (pop[indice].getAptidao() < pivo.getAptidao()) {
pop[topo] = pop[indice];
pop[indice] = pop[topo + 1];
topo++;
}
}
pop[topo] = pivo;
meio = topo;
QuickSort(pop, inicio, meio);
QuickSort(pop, meio + 1, fim);
}
return pop;
}
public ArrayList<Individuo> cruzamento(ArrayList<Individuo> populacaoA)
throws IOException {
int tamanhoPop = populacaoA.size();
Individuo[] populacao = new Individuo[tamanhoPop];
populacao = populacaoA.toArray(populacao);
populacaoA.clear();
String[] indPai1,indPai2, indFilho1, indFilho2;
int pp = 3, sp = 7, k, c1, c2;
int tamanhoSecao = (int) tamanhoIndividuo/2;
Random r = new Random();
boolean presente;
for (int i = 0; i < tamanhoPop; i += 2) {
indFilho1 = new String[tamanhoIndividuo];
indFilho2 = new String[tamanhoIndividuo];
pp = r.nextInt(tamanhoSecao - 1);
sp = pp+tamanhoSecao;
if (i + 1 < tamanhoPop) {
indPai1 = populacao[i].getIndArray();
indPai2 = populacao[i + 1].getIndArray();
for (int c = pp; c <= sp; c++) {
indFilho1[c] = indPai1[c];
indFilho2[c] = indPai2[c];
}
c1 = sp + 1;
c2 = sp + 1;
for (int j=sp+1; j!=pp; j=(j + 1)%tamanhoIndividuo) {
do {
presente = false;
for (k = pp; k <= sp; k++) {
presente |= indPai2[c2].equals(indFilho1[k]);}
if (!presente) {indFilho1[j] = indPai2[c2];}
c2 = (c2 + 1) % tamanhoIndividuo;

89
} while (presente);
do {
presente = false;
for (k = pp; k <= sp; k++) {
presente |= indPai1[c1].equals(indFilho2[k]);}
if (!presente) {indFilho2[j] = indPai1[c1];}
c1 = (c1 + 1) % tamanhoIndividuo;
} while (presente);
}
Individuo indF1 = new Individuo();
Individuo indF2 = new Individuo();
indF1.setIndArray(indFilho1);
indF2.setIndArray(indFilho2);
populacaoA.add(indF1);
populacaoA.add(indF2);
} else {
populacaoA.add(populacao[i]);
}
}
return populacaoA;
}
public ArrayList<Individuo> mutacao(ArrayList<Individuo> populacao) throws
IOException {
int tamanhoPop = populacao.size();
String cidade;
String[] indString;
Individuo indi;
Random indRandom = new Random();
int ri, rc1, rc2;
if(tamanhoPop == 1){taxaMutacao = 1;}
for (int i = 0; i < tamanhoPop * taxaMutacao; i++) {
ri = indRandom.nextInt(tamanhoPop);
indi = populacao.get(ri);
indString = indi.getIndArray();
rc1 = indRandom.nextInt(tamanhoIndividuo);
rc2 = indRandom.nextInt(tamanhoIndividuo);
cidade = indString[rc1];
indString[rc1] = indString[rc2];
indString[rc2] = cidade;
indi.setIndArray(indString);
populacao.set(ri, indi);
}
return populacao;
}
public Individuo getMelhorIndividuo() {return melhorIndividuo;}
public void setMelhorIndividuo(Individuo ind) {
if (getMelhorIndividuo().getAptidao() == 0
|| getMelhorIndividuo().getAptidao()
> ind.getAptidao()){
Individuo MelhorInd = new Individuo();
MelhorInd.setCromossomo(ind.getCromossomo());
MelhorInd.setAptidao(ind.getAptidao());
this.melhorIndividuo = MelhorInd;
}
}
public double getTaxaMutacao(){return this.taxaMutacao;}
public void setTaxaMutacao(double taxa){this.taxaMutacao = taxa; }
}

Aplicação da Técnica Mapreduce na Modelagem de Algoritmos Genéticos para o “Problema do Caixeiro Viajante”

Mais conteúdo relacionado

Destaque

Aplicação da Técnica Mapreduce na Modelagem de Algoritmos Genéticos para o “Problema do Caixeiro Viajante”