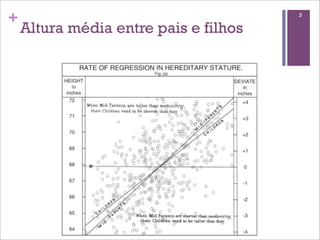
O documento discute modelagem estatística linear e p-values. Ele apresenta um modelo de regressão linear entre a altura dos pais e filhos, simula amostras deste modelo, e discute como p-values podem ser usados para testar hipóteses sobre os coeficientes do modelo à medida que o tamanho da amostra aumenta.

1. +
Bioestatística - Universidade Católica de Brasília
Inferências e P-values
Prof. Dr. Gabriel da Rocha Fernandes
Universidade Católica de Brasília
gabrielf@ucb.br - fernandes.gabriel@gmail.com

2. +
Modelagem estatística
2
nDescrever a distribuição das variáveis.
nDescrever a relação entre as variáveis.
nFazer inferências sobre distribuições ou relações.

3. +
Altura média entre pais e filhos
3

4. +
Modelo linear
nCarregando os dados:
n install.packages('UsingR')
n library('UsingR')
n data(galton)
nObservando os dados:
n hist(galton$child,col="blue",breaks=100)
n hist(galton$parent,col="blue",breaks=100)
nE se eu só sei a média?
n hist(galton$child,col="blue",breaks=100)
n meanChild <- mean(galton$child)
n lines(rep(meanChild,100),seq(0,150,length=100),col="red",lwd=5)
4

5. +
Modelando
nObserve os pontos:
n plot(galton$parent,galton$child,pch=19,col="blue")
n smoothScatter(galton$parent,galton$child)
nEncontrando os modelo:
n lm1 <- lm(galton$child ~ galton$parent)
n lines(galton$parent,lm1$fitted,col="red",lwd=3)
nEquação de uma linha:
n y = a + bx
nNem todos os pontos estão na linha, isso pode ser explicado
por outras variávies residuais (alimentação, esportes...)
n y = a + bx + e
5

6. +
O que fica de fora da linha?
nResíduo.
n smoothScatter(galton$parent,lm1$residuals)
n abline(c(0,0),col="red",lwd=3)
nQuais os coeficientes:
n lm1
nEquação final:
n Altura da criança = 23.942 + 0.646 * Altura do Pai
6

7. +
Simulação
nGerando 1 milhão de famílias:
n newGalton <- data.frame(parent=rep(NA,1e6),child=rep(NA,1e6))
n newGalton$parent <- rnorm(1e6,mean=mean(galton
$parent),sd=sd(galton$parent))
n newGalton$child <- lm1$coeff[1] + lm1$coeff[2]*newGalton$parent +
rnorm(1e6,sd=sd(lm1$residuals))
n smoothScatter(newGalton$parent,newGalton$child)
n abline(lm1,col="red",lwd=3)
nSubamostra:
n set.seed(134325)
n sampleGalton1 <- newGalton[sample(1:1e6,size=50,replace=F),]
n sampleLm1 <- lm(sampleGalton1$child ~ sampleGalton1$parent)
n plot(sampleGalton1$parent,sampleGalton1$child,pch=19,col="blue")
n lines(sampleGalton1$parent,sampleLm1$fitted,lwd=3,lty=2)
n abline(lm1,col="red",lwd=3)
7

8. +
Muitas subamostras
nGerando:
n sampleLm <- vector(100,mode="list")
n for(i in 1:100){
sampleGalton <- newGalton[sample(1:1e6,size=50,replace=F),]
sampleLm[[i]] <- lm(sampleGalton$child ~ sampleGalton$parent)
}
nO que posso inferir sobre meu modelo (linha vermelha), se o
que eu tenho quando faço subamostras é isso:
n smoothScatter(newGalton$parent,newGalton$child)
n for(i in 1:100){abline(sampleLm[[i]],lwd=3,lty=2)}
n abline(lm1,col="red",lwd=3)
8

9. +
Histogramas das estimativas (a e b)
nHistograma de a:
n hist(sapply(sampleLm,function(x){coef(x)
[1]}),col="blue",xlab="Intercept",main="")
nHistograma de b:
n hist(sapply(sampleLm,function(x){coef(x)
[2]}),col="blue",xlab="Slope",main="")
nb0 ∼ N(b0,Var(b0))
9

10. +
Estimando os valores em R
nEntendendo um modelo linear:
n sampleGalton4 <- newGalton[sample(1:1e6,size=50,replace=F),]
n sampleLm4 <- lm(sampleGalton4$child ~ sampleGalton4$parent)
n summary(sampleLm4)
nObservando as diferenças entra a população e a amostra:
n hist(sapply(sampleLm,function(x){coef(x)
[2]}),col="blue",xlab="Slope",main="",freq=F)
n lines(seq(0,5,length=100),dnorm(seq(0,5,length=100),mean=coef(sam
pleLm4)[2], sd=summary(sampleLm4)$coeff[2,2]),lwd=3,col="red")
10

11. +
Intervalos de confiança
n Se temos uma estimativa b, e queremos saber quão bom esta
estimativa é.
n Um jeito é criar um nivel de confiança.
n Fazendo:
n summary(sampleLm4)$coeff
n confint(sampleLm4,level=0.95)
n Vendo:
n par(mar=c(4,4,0,2));plot(1:10,type="n",xlim=c(0,1.5),ylim=c(0,100),
xlab="Coefficient Values",ylab="Replication")
n for(i in 1:100){
n ci <- confint(sampleLm[[i]]); color="red";
n if((ci[2,1] < lm1$coeff[2]) & (lm1$coeff[2] < ci[2,2])){color = "grey"}
n segments(ci[2,1],i,ci[2,2],i,col=color,lwd=3)}
n lines(rep(lm1$coeff[2],100),seq(0,100,length=100),lwd=3)
11

12. +
P-value
nPrincipal medida de significância estatística.
nComumente citado em artigos.
nUsado para tomada de decisões.
nControverso entre os estatísticos.
nSuponha que nada tenha acontecido. Quão incomum é ver as
estimativas que obtivemos?
nAbordagens:
n Definir uma distribuição hipotética de um dado quando nada está
acontecendo (hipótese nula)
n Calcular a estatística com os dados que obtivemos.
n Comparar os valores calculados.
12

13. nSeus dados obedecem a uma distribuição:
nH0: Não há relação entre a altura do pai e do filho (b1=0).
nSob essa hipótese, temos:
nSimulando uma distribuição nula:
n x <- seq(-20,20,length=100)
n plot(x,dt(x,df=(928-2)),col="blue",lwd=3,type="l")
nEstatística observada:
n arrows(summary(lm1)$coeff[2,3],0.25,summary(lm1)$coeff[2,3],
0,col="red",lwd=4)
+
Hipoteses
13

14. +
Exemplo simulado
n Regressão linear:
n set.seed(9898324)
n yValues <- rnorm(10); xValues <- rnorm(10)
n lm2 <- lm(yValues ~ xValues)
n summary(lm2)
n Comparando:
n x <- seq(-5,5,length=100)
n plot(x,dt(x,df=(10-2)),col="blue",lwd=3,type="l")
n arrows(summary(lm2)$coeff[2,3],0.25,summary(lm2)$coeff[2,3],0,col="red",lwd=4)
n Marcando:
n xSequence <- c(seq(summary(lm2)$coeff[2,3],
5,length=10),summary(lm2)$coeff[2,3])
n ySequence <- c(dt(seq(summary(lm2)$coeff[2,3],5,length=10),df=8),0)
n polygon(xSequence,ySequence,col="red"); polygon(-
xSequence,ySequence,col="red")
14

15. +
Tamanho da amostra e P-value
n Amostra simulada:
n set.seed(8323); pValues <- rep(NA,100)
n for(i in 1:100){xValues <- rnorm(20);yValues <- rnorm(20); pValues[i] <-
summary(lm(yValues ~ xValues))$coeff[2,4] }
n hist(pValues,col="blue",main="",freq=F)
n abline(h=1,col="red",lwd=3)
n Adicionando um vies:
n set.seed(8323); pValues <- rep(NA,100)
n for(i in 1:100){xValues <- rnorm(20); yValues <- 0.2 * xValues + rnorm(20); pValues[i] <-
summary(lm(yValues ~ xValues))$coeff[2,4] }
n hist(pValues,col="blue",main="",freq=F)
n abline(h=1,col="red",lwd=3)
n Adicionando amostras:
n set.seed(8323); pValues <- rep(NA,100)
n for(i in 1:100){xValues <- rnorm(100); yValues <- 0.2 * xValues + rnorm(100); pValues[i] <-
summary(lm(yValues ~ xValues))$coeff[2,4] }
n hist(pValues,col="blue",main="",freq=F)
n abline(h=1,col="red",lwd=3)
15