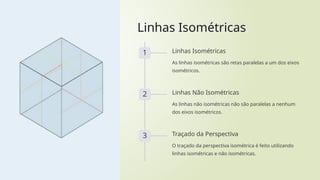
O documento fornece uma introdução às figuras geométricas, explicando conceitos como pontos, linhas e sólidos geométricos, além de descrever as diferentes formas de perspectiva, especialmente a isométrica. Ele detalha a importância da perspectiva isométrica em desenhos técnicos e apresenta instruções sobre como traçar essa perspectiva com precisão. Finalmente, o texto inclui exercícios práticos para ajudar os leitores a dominar o traçado da perspectiva isométrica.