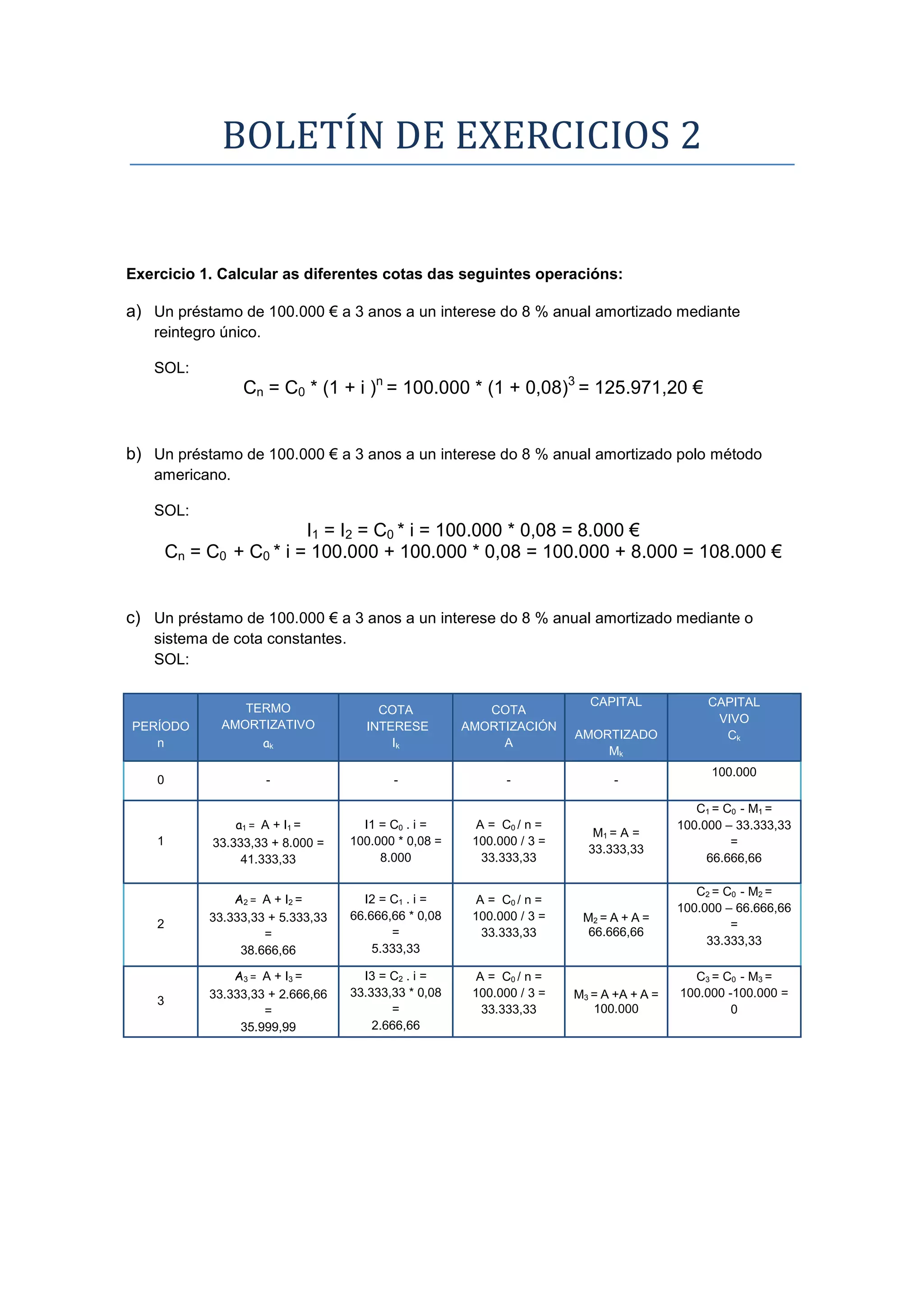
1) O documento apresenta vários exercícios de cálculo de juros e amortização de empréstimos com diferentes taxas de juros e métodos de pagamento. 2) Inclui cálculos para empréstimos de 3 anos a 8% de juros anual com pagamento único, método americano e cota constante. 3) Também determina o montante a pagar em 8 anos para um empréstimo de 50.000€ a 6% e as variáveis para um empréstimo de 200.000€ a 8% por 10 anos pelo método americano

1. BOLETIN DE EXERCICIOS 2
Exercicio 1. Calcular as diferentes cotas das seguintes operacións:
a) Un préstamo de 100.000 € a 3 anos a un interese do 8 % anual amortizado mediante
reintegro único.
SOL:
Cn = C0 * (1 + i )n = 100.000 * (1 + 0,08)3 = 125.971,20 €
b) Un préstamo de 100.000 € a 3 anos a un interese do 8 % anual amortizado polo método
americano.
SOL:
I1 = I2 = C0 * i = 100.000 * 0,08 = 8.000 €
Cn = C0 + C0 * i = 100.000 + 100.000 * 0,08 = 100.000 + 8.000 = 108.000 €
c) Un préstamo de 100.000 € a 3 anos a un interese do 8 % anual amortizado mediante o
sistema de cota constantes.
SOL:
CAPITAL CAPITAL
TERMO COTA COTA
AMORTIZATIVO VIVO
PERÍODO INTERESE AMORTIZACIÓN
AMORTIZADO Ck
n ak Ik A
Mk
100.000
0 - - - -
C1 = C0 - M1 =
a1 = A + I1 = I1 = C0 . i = A = C0 / n = 100.000 – 33.333,33
M1 = A =
1 33.333,33 + 8.000 = 100.000 * 0,08 = 100.000 / 3 = =
33.333,33
41.333,33 8.000 33.333,33 66.666,66
C2 = C0 - M2 =
A2 = A + I 2 = I2 = C1 . i = A = C0 / n =
100.000 – 66.666,66
33.333,33 + 5.333,33 66.666,66 * 0,08 100.000 / 3 = M2 = A + A =
2 =
= = 33.333,33 66.666,66
33.333,33
38.666,66 5.333,33
A3 = A + I 3 = I3 = C2 . i = A = C0 / n = C3 = C0 - M3 =
33.333,33 + 2.666,66 33.333,33 * 0,08 100.000 / 3 = M3 = A +A + A = 100.000 -100.000 =
3
= = 33.333,33 100.000 0
35.999,99 2.666,66

2. d) Determinar o montante a devolver dentro de 8 anos por un préstamo de 50.000 € pactando a
operación ó 6 %.
SOL:
an = Cn = C0 * (1 + i)n = 50 000 * (1 + 0, 06)8 = 79.692, 40 €
e) Determinar as variables dun préstamo de 200.000 € amortizado polo sistema americano se i
= 8% e terá unha duración de 10 años.
I1 = I2 = · · · = I10 = 200.000 * 0, 08 = 16.000 €
a1 = a2 = · · · = a9 = C0 * i = 200.000 * 0, 08 = 16.000 €
a10 = C0 + C0 * i = 200.000 + 16.000 = 216.000 €