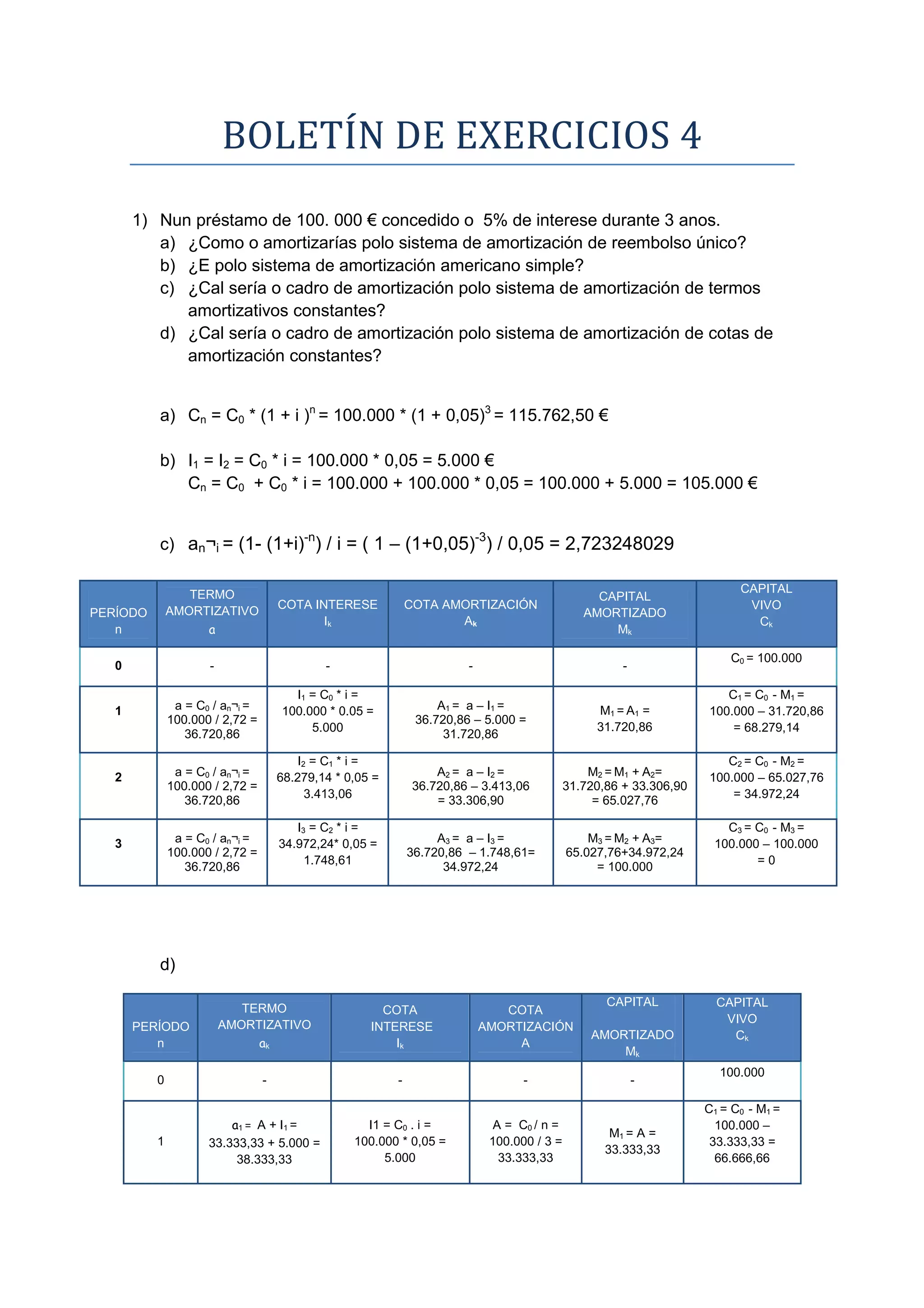
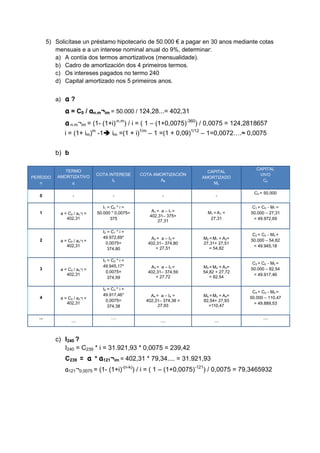
O documento apresenta vários exercícios sobre amortização de empréstimos utilizando diferentes métodos como amortização única, americano simples, termos amortizativos constantes e cotas de amortização constantes. Calcula valores como capital, juros, amortização para cada período, dados os parâmetros do empréstimo como capital inicial, taxa de juros e prazo.

1. BOLETIN DE EXERCICIOS 4
1) Nun préstamo de 100. 000 € concedido o 5% de interese durante 3 anos.
a) ¿Como o amortizarías polo sistema de amortización de reembolso único?
b) ¿E polo sistema de amortización americano simple?
c) ¿Cal sería o cadro de amortización polo sistema de amortización de termos
amortizativos constantes?
d) ¿Cal sería o cadro de amortización polo sistema de amortización de cotas de
amortización constantes?
a) Cn = C0 * (1 + i )n = 100.000 * (1 + 0,05)3 = 115.762,50 €
b) I1 = I2 = C0 * i = 100.000 * 0,05 = 5.000 €
Cn = C0 + C0 * i = 100.000 + 100.000 * 0,05 = 100.000 + 5.000 = 105.000 €
c) an¬i = (1- (1+i)-n) / i = ( 1 – (1+0,05)-3) / 0,05 = 2,723248029
TERMO CAPITAL
CAPITAL
COTA INTERESE COTA AMORTIZACIÓN VIVO
PERÍODO AMORTIZATIVO AMORTIZADO
Ik Ak Ck
n a Mk
C0 = 100.000
0 - - - -
I1 = C0 * i = C1 = C0 - M1 =
1 a = C0 / an¬i = 100.000 * 0.05 = A1 = a – I1 = M1 = A1 = 100.000 – 31.720,86
100.000 / 2,72 = 36.720,86 – 5.000 =
5.000 31.720,86 = 68.279,14
36.720,86 31.720,86
I2 = C1 * i = C2 = C0 - M2 =
2 a = C0 / an¬i = 68.279,14 * 0,05 = A2 = a – I2 = M2 = M1 + A2= 100.000 – 65.027,76
100.000 / 2,72 = 36.720,86 – 3.413,06 31.720,86 + 33.306,90
3.413,06 = 34.972,24
36.720,86 = 33.306,90 = 65.027,76
I3 = C2 * i = C3 = C0 - M3 =
3 a = C0 / an¬i = 34.972,24* 0,05 = A3 = a – I3 = M3 = M2 + A3= 100.000 – 100.000
100.000 / 2,72 = 36.720,86 – 1.748,61= 65.027,76+34.972,24
1.748,61 =0
36.720,86 34.972,24 = 100.000
d)
CAPITAL CAPITAL
TERMO COTA COTA
AMORTIZATIVO VIVO
PERÍODO INTERESE AMORTIZACIÓN
AMORTIZADO Ck
n ak Ik A
Mk
100.000
0 - - - -
C1 = C0 - M1 =
a1 = A + I1 = I1 = C0 . i = A = C0 / n = 100.000 –
M1 = A =
1 33.333,33 + 5.000 = 100.000 * 0,05 = 100.000 / 3 = 33.333,33 =
33.333,33
38.333,33 5.000 33.333,33 66.666,66

2. C2 = C0 - M2 =
A2 = A + I 2 = A = C0 / n =
I2 = C1 . i = 100.000 –
33.333,33 + 100.000 / 3 = M2 = A + A =
2 66.666,66 * 0,05 = 66.666,66 =
3.333,33 = 33.333,33 66.666,66
3.333,33 33.333,33
36.666,66
C3 = C0 - M3 =
A3 = A + I 3 = A = C0 / n =
I3 = C2 . i = 100.000 -100.000
33.333,33 + 100.000 / 3 = M3 = A +A + A =
3 33.333,33 * 0,05 = =
1.666,66 = 33.333,33 100.000
1.666,66 0
34.999,99
2) Préstanse 500.000 € ó 8% efectivo anual, para devolver en 10 anos mediante
termos amortizativos anuais constantes. Calcula:
a) A anualidade
b) O capital pendente de amortizar o final do quinto ano.
c) O capital amortizado nos catro primeiros anos.
d) A cota de amortización do oitavo ano.
e) A cota de interese do terceiro ano.
a) a?
a = C0 / an¬i = 500.000 / 6,710081399 = 74.514,74
an¬i = (1- (1+i)-n) / i = ( 1 – (1+0,08)-10) / 0,08 = 6,710081399
b) C5 ?
Ck = a * an-k¬i = 74.514,74 * 3,992710037 =297.515,75
an-k¬i = (1- (1+i)-(n-k)) / i = ( 1 – (1+0,08)-5) / 0,08 = 3,992710037
c) M4 ?
Mk = C0 - Ck = 500.000 - 344.472,68 = 155.527,33
C4 = a * an-k¬i = 74.514,74 * 4,622879664 = 344.472,68
an-k¬i = (1- (1+i)-(n-k)) / i = ( 1 – (1+0,08)-6) / 0,08 = 4,622879664
d) A8 ?
Ak = A1 *(1+i )k-1 = 34.514,74 * (1+0,08 )7 = 59.152,20
A 1 = a - I 1 = a - c0 * i
A1 = 74.514,74 – (500.000 * 0,08) = 74.514,74 – 40.000 = 34.514,74
e) I3 ?
Ik = a - Ak = 74.514,74 - 40.257,99 = 34.256,74
A3 = A1 *(1+i )2 = 34.514,74 * (1+0,08 )2 = 40.257,99

3. 3) Concédese un préstamo de 2 millóns de euros para ser amortizado en 10 anos a
un tipo de interese do 9 % anual. Calcula o termo amortizativo se:
a) Durante os 3 primeiros anos so se pagan intereses e nos restantes unha
anualidade constante.
SOL:
- 3 primeiros anos:
a = c0 * i = 2.000.000 * 0,09 = 180.000
- Restantes 7 anos:
C3 = C0 = a * an-k¬i
a = C0 / an¬i = 2.000.000 / 5,032952835 =397.381,03
an¬i = (1- (1+i)-n) / i = ( 1 – (1+0,09)-7) / 0,09 = 5,032952835
4) Fai catro anos concedeuse un préstamo amortizable polo método Francés ó 6%
anual. Se o capital pendente de amortizar hoxe é de 804.393 € e a cota de
amortización do quinto período será 70.000 €. Determina:
a) O capital que se prestou.
b) A duración da operación.
a) C0 ?
C0 = C4 + M4 = 804.393 + 242.557,41 =1.046.950,41
Mk = A1 + A2 + A3 +... + Ak = A1 * Sk¬i
M4 = A1 * S4¬i = 55.446,56 * ((1+0,06)4 -1)/ 0,09 = 242.557,41
A5 = A1 *(1+i )4 A1 = A5 / (1+i )4 = 70.000 /(1+0,06)4 = 55.446,56
b) n?
C0 = a * an-k¬i an-k¬i = C0 /a = 1.046.950,41 / 118.263,58 = 8,8526
(1- (1+0,06)-n) / 0,06 = 8,8526
-(1,06)-n = 8,8526 * 0,06 -1= - 0,468844
(1,06)-n = 0,468844
-n * lg1,06 = lg 0,468844
-n = lg 0,468844/ lg1,06 = -0,32897 / 0,0253
-n = -12,9999 ≈ -13
n = 12,9999 ≈ 13
a= A5 + I5 = 70.000 + 48.263,58 = 118.263,58
I5 = C4 * i = 804.393 * 0.06 = 48.263,58

4. 5) Solicítase un préstamo hipotecario de 50.000 € a pagar en 30 anos mediante cotas
mensuais e a un interese nominal anual do 9%, determinar:
a) A contía dos termos amortizativos (mensualidade).
b) Cadro de amortización dos 4 primeiros termos.
c) Os intereses pagados no termo 240
d) Capital amortizado nos 5 primeiros anos.
a) a?
a = C0 / an.m¬im = 50.000 / 124,28...= 402,31
a n.m¬im = (1- (1+i)-n.m) / i = ( 1 – (1+0,0075)-360) / 0,0075 = 124,2818657
i = (1+ im)m -1 im =(1 + i)1/m – 1 =(1 + 0,09)1/12 – 1=0,0072….≈ 0,0075
b) b
TERMO CAPITAL
CAPITAL
COTA INTERESE COTA AMORTIZACIÓN VIVO
PERÍODO AMORTIZATIVO AMORTIZADO
Ik Ak Ck
n a Mk
C0 = 50.000
0 - - - -
I1 = C0 * i = C1 = C0 - M1 =
1 50.000 * 0,0075= A1 = a – I1 = M1 = A1 = 50.000 – 27,31
a = C0 / an¬i =
402,31– 375=
402,31 375 27,31 = 49.972,69
27,31
I2 = C1 * i =
C2 = C0 - M2 =
49.972,69* A2 = a – I2 = M2 = M1 + A2=
2 a = C0 / an¬i = 50.000 – 54,82
0,0075= 402,31– 374,80 27,31+ 27,51
402,31 = 49.945,18
374,80 = 27,51 = 54,82
I3 = C2 * i =
C3 = C0 - M3 =
49.945,17* A3 = a – I3 = M3 = M2 + A3=
3 a = C0 / an¬i = 50.000 – 82,54
0,0075= 402,31– 374,59 54,82 + 27,72
402,31 = 49.917,46
374,59 = 27,72 = 82,54
I4 = C3 * i =
C4 = C0 - M4 =
49.917,46* A4 = a – I4 = M4 = M3 + A4=
4 a = C0 / an¬i = 50.000 – 110,47
0,0075= 402,31– 374,38 = 82,54+ 27,93
402,31 = 49.889,53
374,38 27,93 =110,47
... …. ....
.... .... ....
c) I240 ?
I240 = C239 * i = 31.921,93 * 0,0075 = 239,42
C239 = a * a121¬im = 402,31 * 79,34.... = 31.921,93
a121¬0,0075 = (1- (1+i)-(n-k)) / i = ( 1 – (1+0,0075)-121) / 0,0075 = 79,3465932

5. d) M60 ?
M60 = C0 - C60 = 50.000 - 47.939,91= 2.060,09
C60 = a * a300¬0,0075 = 402,31 * 119,16.... = 47.939,91
A300¬0,0075 = (1- (1+0,0075)-300) / 0,0075 = 119,1616222