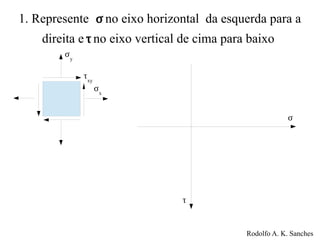
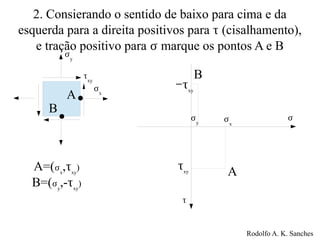
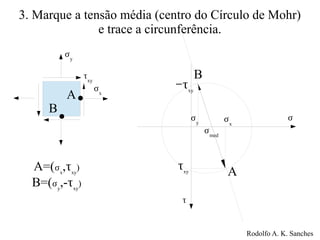
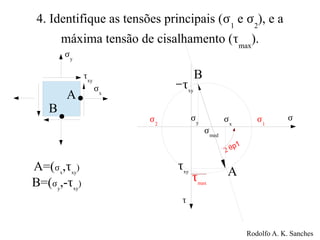
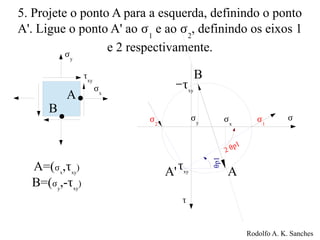
O documento fornece um guia prático para o uso do Círculo de Mohr, que é uma ferramenta gráfica para representar o estado de tensão bidimensional em um ponto. Ele explica como traçar o círculo de Mohr a partir dos valores de tensão normal e cisalhamento, identificar as tensões principais e a máxima tensão de cisalhamento.

1. Círculo de Mohr para o EPT– Guia
prático de utilização
Rodolfo A. K. Sanches

2. 1. Represente sno eixo horizontal da esquerda para a
direita e tno eixo vertical de cima para baixo
sx
sy
txy
s
t
Rodolfo A. K. Sanches

3. 2. Consierando o sentido de baixo para cima e da
esquerda para a direita positivos para t (cisalhamento),
e tração positivo para s marque os pontos A e B
sx
sy
txy
s
t
A
B
A=(sx
,txy
)
B=(sy
,-txy
)
txy
sx
sy
A
B
-txy
Rodolfo A. K. Sanches

4. 3. Marque a tensão média (centro do Círculo de Mohr)
e trace a circunferência.
sx
sy
txy
s
t
A
B
A=(sx
,txy
)
B=(sy
,-txy
)
txy
sx
sy
A
B
-txy
smed
Rodolfo A. K. Sanches

5. 4. Identifique as tensões principais (s1
e s2
), e a
máxima tensão de cisalhamento (tmax
).
sx
sy
txy
s
t
A
B
A=(sx
,txy
)
B=(sy
,-txy
)
txy
sx
sy
A
B
-txy
s1
s2
2 qp1
smed
tmax
Rodolfo A. K. Sanches

6. 5. Projete o ponto A para a esquerda, definindo o ponto
A'. Ligue o ponto A' ao s1
e ao s2
, definindo os eixos 1
e 2 respectivamente.
sx
sy
txy
s
t
A
B
A=(sx
,txy
)
B=(sy
,-txy
)
txy
sx
sy
A
B
-txy
s1
s2
2 qp1
A'
Rodolfo A. K. Sanches
qp1