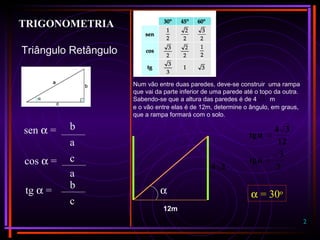
Trigonometria é estudada para resolver problemas envolvendo triângulos retângulos. O documento apresenta definições de seno, cosseno e tangente em termos das proporções entre os lados do triângulo. Também apresenta um exemplo numérico de cálculo de ângulo formado por uma rampa.

1. 1
TRIGONOMETRI
ATRIÂNGULO RETÂNGULO

2. 2
TRIGONOMETRIA
Triângulo Retângulo
sen α =
cos α =
tg α =
b
a
c
a
b
c
Num vão entre duas paredes, deve-se construir uma rampa
que vai da parte inferior de uma parede até o topo da outra.
Sabendo-se que a altura das paredes é de 4 3
e o vão entre elas é de 12m, determine o ângulo, em graus,
que a rampa formará com o solo.
m
12m
34
α
3
3
αtg
12
34
αtg
=
=
α = 30o

3. 3
( UFSC ) Na figura, abaixo, determine o valor de x
3 0 ° 6 0 °
A
B
CD
AD = x DC= x - 38 BD = y
tg 30o
=
x x – 38
y
60o
30o
y
x
3
3 y
x
tg 60o
=
y
x – 38
3 =
x – 38
y
(x – 38) 3 = y
=
3
3
=
(x – 38) 3
x
x = 3(x – 38)
x = 3x – 114
114 = 2x
57 = x

4. 4
TRIGONOMETRI
ASENO COSSENO TANGENTE E
DEMAIS RELAÇÕES
TRIGONOMÉTRICAS

5. 5
SENO E COSSENO E TANGENTE
SENO
+ 1
– 1
+ +
__
COSSENO
+ 1– 1
+
+
_
_
TANGENTE
+
+
_
_
RELAÇÕES TRIGONOMÉTRICAS
sen2
x + cos2
x = 1
tg x =
sen x
cos x
xsen
=xcossec
1
xcos
=xsec
1
xsen
xcos
xtg
=xcotg
1
=

6. 6
a) cos x
sen2
x + cos2
x = 1
1cos
25
16 2
=+ x
25
16
1cos2
−=x
25
9
cos2
=x
5
3
xcos =
1xcos
5
4 2
2
=+





−
tg x =
sen x
cos x
5
3
5
4
xtg
−
=
3
4
xtg −=
b) tg x
c) cotg x
Sendo sen α =
5
4
− e πα
π
2
2
3
<< , calcule:
4
3
xtg
1
xcotg −==
d) sec x
3
5
xcos
1
xsec ==
e) cossec x
4
5
xcos
1
xcossec −==
SENO
+ +
__
COSSENO
+
+
_
_
TANGENTE
+
+
_
_

7. 7
Determine a soma dos números associados às proposições VERDADEIRAS:
π 180o
x 225o
225o
π = x.180o
4
5π
=x
01. A medida em radianos de um arco de 225º
é rad
6
11π
F
02. A equação sen x = 2m – 5 admite solução para 2 ≤ m ≤ 3
– 1 ≤ 2m – 5 ≤ 1
– 1 + 5 ≤ 2m ≤ 1 + 5
4 ≤ 2m ≤ 6
2 ≤ m ≤ 3
V

8. 8
04. Se sen x > 0, então cossec x < 0
sen 30o
= 1/2 cossec 30o
= 2
sen 210o
= - 1/2
F
FP
180o
160o
200o
cossec 210o
= - 2
08. Se tg 20º
= a, o valor de 2-éo
oo
tg200
tg340tg160 +
F
360o
340o
tg 160o
=
tg 200o
=
tg 340o
=
– tg 20o
=
tg 20o
=
– tg 20o
=
– a
a
– a
+
+
_
_
o
oo
tg200
tg340tg160 +
a
a)(a- −+
a
2a−
– 2
V

9. 9
16. Para todo x ∈ 1o
quadrante, a expressão
(sec x – tg x)(sec x + tg x) – sen2
x é igual a cos2
x
(sec x – tg x)(sec x + tg x) – sen2
x
xsen
x
xsen
xx
xsen
x
2
coscos
1
.
coscos
1
−





+





−
xsen
x
xsen
x
xsen 2
cos
1
.
cos
1
−




 +





 −
xsen
x
xsen 2
2
22
cos
1
−




 −
xsen
x
xsen 2
2
2
cos
1
−




 −
xsen
x
x 2
2
2
cos
cos
−





sen2
x + cos2
x = 1
sen2
x = 1 – cos2
x
cos2
x = 1 – sen2
x
1 – sen2
x
cos2
x
V

10. 10
6
π
6
5 π
32. A solução da equação 2sen2
x + 3sen x = 2 para 0 ≤ x ≤ 2π é
x = ou x =
2 sen2
x + 3 sen x – 2 = 0
∆ = b2
– 4ac
∆ = 32
– 4.2.(-2)
∆ = 25
a
b
x
2
∆±−
=
4
53±−
=xsen
2
2
1
−== xsenouxsen
2
1
=xsen
++
30o
150o






=
6
5
,
6
ππ
S
V

11. 11
( UFSC ) Sabendo que cossec x = 5/4 e x é do primeiro quadrante, então o
valor da expressão 9.(sec2
x + tg2
x) é:
cossec x =
4
5
sen x =
5
4
sen2
x + cos2
x = 1
1cos
5
4 2
2
=+





x
1cos
25
16 2
=+ x
25
16
1cos2
−=x
25
9
cos2
=x
5
3
cos =x
3
5
sec =x
tg x =
sen x
cos x
5
3
5
4
=xtg
3
4
=xtg
9.(sec2
x + tg2
x)












+





22
3
4
3
5
9




+
9
16
9
25
9




9
41
9 41

12. 12
TRIGONOMETRI
AOPERAÇÃO COM ARCOS

13. 13
Adição e Subtração de Arcos
sen (a ± b) = sen a . cos b ± sen b . cos a
cos (a ± b) = cos a . cos a sen a . sen b
sen 75º =
sen (30º + 45º) = sen 30º . cos 45º + sen 45º . cos 30º
sen (a + b) = sen a . cos b + sen b. cos a
2
3
.
2
2
2
2
.
2
1
+
sen 75º =
4
62 +
cos 15º =
cos (45º - 30º) = cos 45º . cos 30º + sen 45º . sen 30º
cos (a – b) = cos a . cos b + sen a. sen b
cos 15º =
4
62 +
2
1
.
2
2
2
3
.
2
2
+

14. 14
O valor de cos 10o
cos 35o
– sen 10o
. sen 35º
, é:
sen (a ± b) = sen a . cos b ± sen b . cos a
cos (a ± b) = cos a . cos a sen a . sen b
cos (a + b) = cos a . cos b - sen a. sen b
cos 10o
. cos 35o
– sen 10o
. sen 35ºcos (10º
+ 35o
) =
cos 10o
. cos 35o
– sen 10o
. sen 35º
cos 45o
=
= cos 10o
. cos 35o
– sen 10o
. sen 35º
2
2

15. 15
Seno e Cosseno do arco duplo
sen (a ± b) = sen a . cos b ± sen b . cos a
cos (a ± b) = cos a . cos a sen a . sen b
sen (2x) = 2sen x . cos x
cos (2x) = cos2
x - sen2
x
sen (x + x) = sen x . cos x + sen x . cos x
cos (x + x) = cos x . cos x – sen x . sen x

16. 16
Cálculo do sen x
sen2
x + cos2
x = 1
1
25
16
xsen2
=+
25
16
1xsen2
−=
25
9
xsen2
=
5
3
xsen −=
1
5
4
xsen
2
2
=





+
Sendo cos x =
5
4
e π
π
2
2
3
<< x , calcule sen 2x e cos 2x:
sen (2x) = 2sen x . cos x
cos (2x) = cos2
x - sen2
x
sen (2x) = 











−
5
4
.
5
3
.2
sen (2x) =
25
24
−
cos (2x) =
25
9
25
16
−
cos (2x) =
25
7

17. 17
TRIGONOMETRI
AFUNÇÕES TRIGONOMÉTRICAS
GRÁFICOS

18. 18
FUNÇÕES TRIGONOMÉTRICAS
FUNÇÃO SENO y = sen x
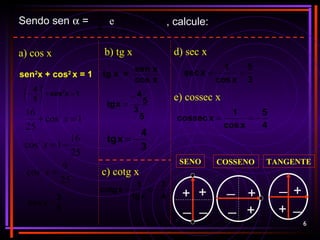
sen x
π
π
π
π
2
2
3
2
0
0 + 1 0 - 1 0
0o
90o
180o
270o
360o
x
x
IMAGEM:
DOMÍNIO: REAIS
[-1, 1]
CRESCENTE:
DECRESCENTE:
1º. e 4º. q
2º. e 3º. q
PERÍODO: 2π

19. 19
FUNÇÕES TRIGONOMÉTRICAS
FUNÇÃO COSSENO y = cos x
cos x
π
π
π
π
2
2
3
2
0
+1 0 - 1 0 +1
0o
90o
180o
270o
360o
x
x
IMAGEM:
DOMÍNIO: REAIS
[-1, 1]
CRESCENTE:
DECRESCENTE:
3º. e 4º. q
1º. e 2º. q
PERÍODO: 2π

20. 20
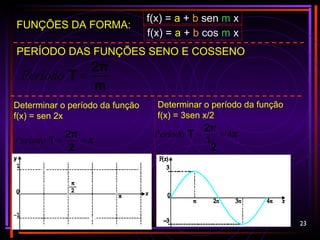
FUNÇÕES DA FORMA:
f(x) = a + b sen m x
f(x) = a + b cos m x
Esboçar o gráfico e dê o período, o domínio e o conjunto
imagem de:
a) y = 2 + sen x
sen x
π
π
π
π
2
2
3
2
0
0 + 1 0 - 1 0
0o
90o
180o
270o
360o
x
x
2 + sen x 2 3 2 1 2
IMAGEM: [1, 3]
PERÍODO: 2π

21. 21
FUNÇÕES DA FORMA:
f(x) = a + b sen m x
f(x) = a + b cos m x
Esboçar o gráfico e dê o período, o domínio e o conjunto
imagem de:
b) y = 3sen x
sen x
π
π
π
π
2
2
3
2
0
0 + 1 0 - 1 0
0o
90o
180o
270o
360o
x
x
3sen x 0 3 0 -3 0
IMAGEM: [-3, 3]
PERÍODO: 2π

22. 22
FUNÇÕES DA FORMA:
f(x) = a + b sen m x
f(x) = a + b cos m x
IMAGEM DA FUNÇÃO SENO E COSSENO: [a – b; a + b]
CONCLUSÕES: a → desloca o gráfico
b → estica o gráfico
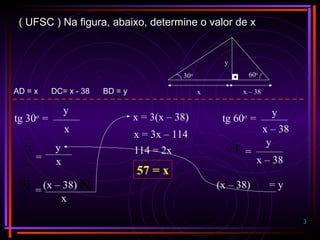
Determinar a imagem da
função f(x) = 2 + 3sen x
f(x) = 2 + 3 sen x
f(x) = 2 + 3 (-1)
f(x) = 2 + 3 (1)
= - 1
= 5
IMAGEM: [-1, 5]
Determinar a imagem da
função f(x) = 5 + 2cos x
f(x) = 5 + 2 cos x
f(x) = 5 + 2 (-1)
f(x) = 5 + 2 (1)
= 3
= 7
IMAGEM: [3, 7]

23. 23
PERÍODO DAS FUNÇÕES SENO E COSSENO
m
2π
T =Período
Determinar o período da função
f(x) = sen 2x
FUNÇÕES DA FORMA:
f(x) = a + b sen m x
f(x) = a + b cos m x
π==
2
2π
TPeríodo
Determinar o período da função
f(x) = 3sen x/2
π4==
2
1
2π
TPeríodo

24. 24
Determine o período da função f(x) = cos4
x – sen4
x é:
Um pouquinho de matemática
básica
(a + b)(a – b) = a2
– b2
(x + 3)(x – 3) = x2
– 9
= x2
– 25(x + 5)(x – 5)
= cos4
x – sen4
x(cos2
x + sen2
x )(cos2
x – sen2
x)
= cos4
x – sen4
x(1)(cos2x)
f(x) = cos4
x – sen4
x
f(x) = cos 2x
π==
2
2π
TPeríodo
m
2π
T =Período
= cos4
x – sen4
xcos2x
fórmulas do arco duplo
sen 2x = 2sen x.cos x
cos 2x = cos2
x – sen2
x

25. 25
FUNÇÕES TRIGONOMÉTRICAS
FUNÇÃO TANGENTE y = tg x
tg x
π
π
π
π
2
2
3
2
0
0 não 0 não 0
existe existe
0o
90o
180o
270o
360o
x
x
IMAGEM:
DOMÍNIO:
REAIS
CRESCENTE: SEMPRE
PERÍODO: π
{x ∈ ℜ|x ≠
2
π
+ kπ}
O domínio da função f(x) = tg 2x é:
24
2
2
2
2
ππ
π
π
π
π
k
x
k
x
kx
+≠
+
≠
+≠