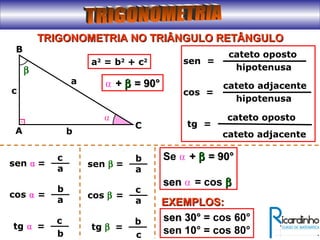
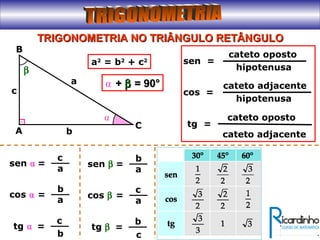
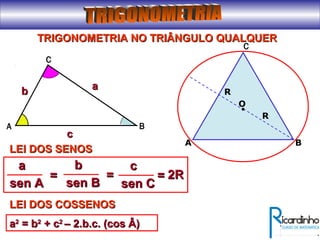
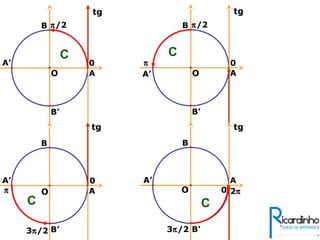
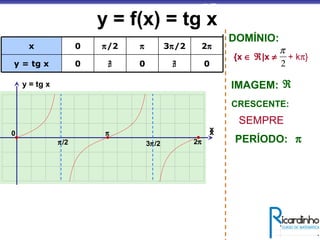
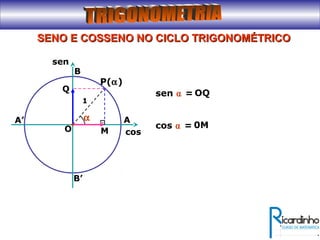
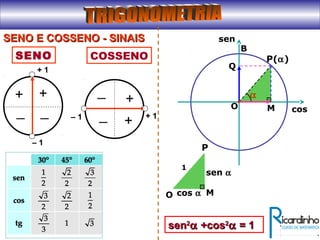
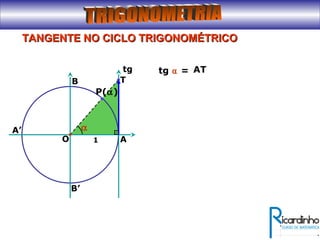
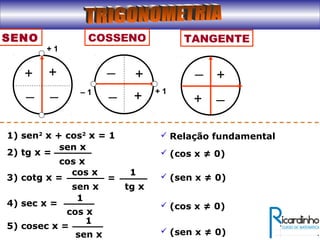
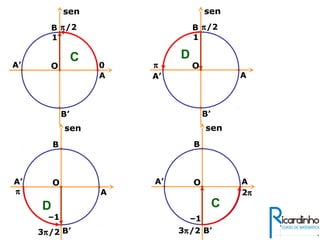
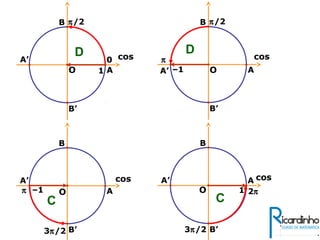
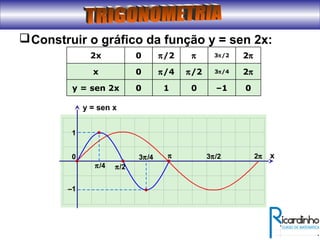
1) O documento apresenta as principais relações trigonométricas nos triângulos retângulo e qualquer; 2) Apresenta as leis dos seno e cosseno para cálculo de lados e ângulos em triângulos; 3) Explica a representação dos valores de seno, cosseno e tangente no ciclo trigonométrico.

2. TRIGONOMETRIA NO TRIÂNGULO RETÂNGULOTRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
A
B
C
a
b
c
a2
= b2
+ c2
⍺
=sen ⍺
c
a
=cos ⍺
b
a
β
=tg ⍺
c
b
⍺ ++ ββ = 90°= 90°
cateto oposto
hipotenusa
sen =
cateto adjacente
hipotenusa
cos =
cateto oposto
tg =
cateto adjacente
=sen β
b
a
=cos β
c
a
=tg β
b
c
Se ⍺ ++ ββ = 90°= 90°
sensen ⍺ = cos ββ
EXEMPLOS:EXEMPLOS:
sen 30°sen 30° = cos 60°
sen 10° = cos 80°

3. TRIGONOMETRIA NO TRIÂNGULO RETÂNGULOTRIGONOMETRIA NO TRIÂNGULO RETÂNGULO
A
B
C
a
b
c
⍺
=sen ⍺
c
a
=cos ⍺
b
a
β
=tg ⍺
c
b
cateto oposto
hipotenusa
sen =
cateto adjacente
hipotenusa
cos =
cateto oposto
tg =
cateto adjacente
=sen β
b
a
=cos β
c
a
=tg β
b
c
a2
= b2
+ c2
⍺ ++ ββ = 90°= 90°

4. TRIGONOMETRIA NO TRIÂNGULO QUALQUERTRIGONOMETRIA NO TRIÂNGULO QUALQUER
A
C
B
cc
aa
bb
aa
sen Asen A
== 2R2R
LEI DOS SENOSLEI DOS SENOS
bb
sen Bsen B
==
cc
sen Csen C
==
O
A B
R
C
R
LEI DOS COSSENOSLEI DOS COSSENOS
aa22
= b= b22
+ c+ c22
– 2.b.c. (cos Â)– 2.b.c. (cos Â)

5. SENO E COSSENO NO CICLO TRIGONOMÉTRICOSENO E COSSENO NO CICLO TRIGONOMÉTRICO
B’
A’
O
A
B
P(α)
α
M
Q
sen ⍺ =
1
OQ
cos ⍺ = 0M
cos
sen

6. SENO E COSSENO NO CICLO TRIGONOMÉTRICOSENO E COSSENO NO CICLO TRIGONOMÉTRICO
sen 0º = sen 0 =
cos 0º = cos 0 =
(–1, 0)A’ A(1,0)
B(0, 1)π/2
0 ou 2ππ
O
3π/2 B’(0, –1)
A(1, 0)
0
⇒
1
sen 90º = sen π/2
=
cos 90º = cos π/2 =
B(0, 1)
1
⇒
0
sen 180º = sen π =
cos 180º = cos π =
A’(–1, 0)
0
⇒
–1

7. SENO E COSSENO NO CICLO TRIGONOMÉTRICOSENO E COSSENO NO CICLO TRIGONOMÉTRICO
(–1, 0)A’ A(1,0)
B(0, 1)π/2
0 ou 2ππ
O
3π/2 B’(0, –1)
sen 270º = sen 3π/2 =
cos 270º = cos 3π/2 =
B’(0,–1)
–1
⇒
0
sen 360º = sen 2π
=
cos 360º = cos 2π =
A(1, 0)
0
⇒
1

8. SENO E COSSENO - SINAISSENO E COSSENO - SINAIS
SENO
+ 1
– 1
+ +
__
COSSENO
+ 1– 1
+
+
_
_
O
B
P(α)
α
M
Q
cos
sen
O
P
M
1
cos α
sen α
sensen22
αα +cos+cos22
αα = 1= 1

9. B’
A’
O A
B
P(α)
α
1
T
tg ⍺ = ATtg
TANGENTE NO CICLO TRIGONOMÉTRICOTANGENTE NO CICLO TRIGONOMÉTRICO

10. SENO
+ 1
+ +
__
COSSENO
+ 1– 1
+
+
_
_
TANGENTE
+
+
_
_
1) sen2
x + cos2
x = 1  Relação fundamental
2) tg x =
sen x
cos x
 (cos x ≠ 0)
3) cotg x =
cos x
sen x
 (sen x ≠ 0)=
1
tg x
4) sec x =
1
cos x
 (cos x ≠ 0)
5) cosec x =
1
sen x  (sen x ≠ 0)

11. Adição e Subtração de Arcos
sen (a ± b) = sen a . cos b ± sen b . cos a
cos (a ± b) = cos a . cos b sen a . sen b
sen 75º =
sen (30º + 45º) = sen 30º . cos 45º + sen 45º . cos 30º
sen (a + b) = sen a . cos b + sen b. cos a
2
3
.
2
2
2
2
.
2
1
+
sen 75º =
4
62 +
cos 15º =
cos (45º - 30º) = cos 45º . cos 30º + sen 45º . sen 30º
cos (a – b) = cos a . cos b + sen a. sen b
cos 15º =
4
62 +
2
1
.
2
2
2
3
.
2
2
+

12. O valor de cos 10o
cos 35o
– sen 10o
. sen 35º
, é:
cos (a + b) = cos a . cos b - sen a. sen b
cos 10o
. cos 35o
– sen 10o
. sen 35ºcos (10º
+ 35o
) =
cos 10o
. cos 35o
– sen 10o
. sen 35º
cos 45o
=
= cos 10o
. cos 35o
– sen 10o
. sen 35º
2
2
sen (a ± b) = sen a . cos b ± sen b . cos a
cos (a ± b) = cos a . cos b sen a . sen b

13. Seno e Cosseno do arco duplo
sen (2x) = 2sen x . cos x
cos (2x) = cos2
x - sen2
x
sen (x + x) = sen x . cos x + sen x . cos x
cos (x + x) = cos x . cos x – sen x . sen x
sen (a ± b) = sen a . cos b ± sen b . cos a
cos (a ± b) = cos a . cos b sen a . sen b

14. O 0
B
A’
B’
π/2
A
sen
1
Oπ
B
A’
B’
π/2
A
sen
1
O
π
B
A’
B’3π/2
A
sen
–1
O A
B
A’
B’3π/2
2π
sen
–1
C D
D C

15. y = f(x) = sen x
0
π
0–110y = sen x
2π3π/2π/20x
x
y = sen x
0
π/2
1
–1
π
3π/2 2π
IMAGEM:
DOMÍNIO: ℜ
[-1, 1]
CRESCENTE:
DECRESCENTE:
1º. e 4º. q
2º. e 3º. q
PERÍODO: 2π

16. Construir o gráfico da função y = 1 + sen x:
1
0
π
1021y = 1 + sen x
0–110sen x
2π3π/2π/20x
x
y
0
π/2
1
–1
π 3π/2 2π
2
–2
 y = sen x  y = 1 + sen x
p = 2π
Im = [–1, 1]
p = 2π
Im = [0, 2]

17. Construir o gráfico da função y = 2 sen x:
0
0
π
0–220y = 2 sen x
0–110sen x
2π3π/2π/20x
x
y
0
π/2
1
–1
π
3π/2
2π
2
–2
 y = sen x  y = 2sen x
p = 2π
Im = [–1, 1]
p = 2π
Im = [–2, 2]

18. O
0
B
A’
B’
π/2
A
cos
1 O
π
B
A’
B’
π/2
A
cos
–1
Oπ
B
A’
B’3π/2
A
cos
–1 O
A
B
A’
B’3π/2
2π
cos
1
D D
C C

19. y = f(x) = cos x
–1
π
1001y = cos x
2π3π/2π/20x
x
y = cos x
0
π/2
1
–1
π
3π/2 2π
IMAGEM:
DOMÍNIO: ℜ
[-1, 1]
CRESCENTE:
DECRESCENTE:
3º. e 4º. q
1º. e 2º. q
PERÍODO: 2π

20. Construir o gráfico da função y = sen 2x:
0
π/2
π
0–110y = sen 2x
2π3π/4π/40x
2π3π/2π/202x
x
y = sen x
0
π/2
1
–1
π 3π/2 2π
π/4
3π/4

21. [–2, 0]4πℝy = - 1 + sen (x/2)
[-1, 3]2π/3ℝy = 1 + 2cos (3x + π/2)
[–3, 1]2πℝy = –1 + 2sen (x + π/2)
[–2, 4]πℝy = 1 + 3sen (2x)
2π
2π
2π
2π
2π
Período
[2, 4]ℝy = 3 + cos (x)
[–1, 1]ℝy = cos (x)
[4, 8]ℝy = 6 + 2 sen (x)
[1, 7]ℝy = 4 + 3sen (x)
[–1, 1]ℝy = sen (x)
ImagemDomínioFunção
f(x) = a + b sen m x
f(x) = a + b cos m x

22. O
0
B
A’
B’
π/2
A
tg
O
π
B
A’
B’
π/2
A
tg
0
Oπ
B
A’
B’3π/2
A
tg
0
O
A
B
A’
B’3π/2
2π
tg
0
C C
C C

23. 0
π
0∄∄0y = tg x
2π3π/2π/20x
x
y = tg x
0
π/2
π
3π/2 2π
y = f(x) = tg x
x
IMAGEM:
DOMÍNIO:
ℜ
CRESCENTE:
SEMPRE
PERÍODO: π
{x ∈ ℜ|x ≠
2
π
+ kπ}