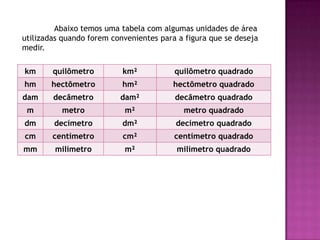
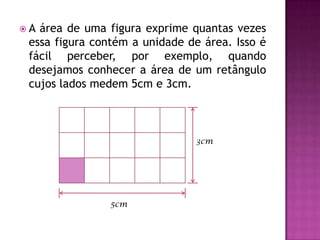
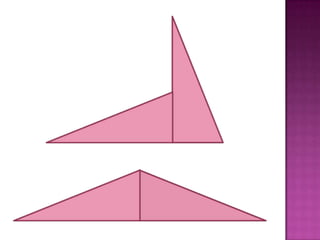
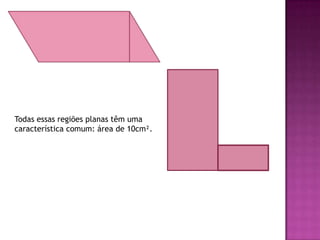
O documento define área como a porção do plano ocupada por uma figura geométrica e explica que medir a área significa compará-la com uma unidade de área, como um quadrado de lado 1 cm (cm2). O documento fornece exemplos de como calcular a área de retângulos e equivalentes de áreas entre diferentes formas geométricas que possuem a mesma área total.

1. ÁREA DE UMA SUPERFÍCIE

2. ÁREAMedir uma grandeza significa compará-la com outra de mesma espécie tomada como unidade.A área é a porção do plano ocupada por uma figura. Para encontrarmos a área de uma figura devemos comparar sua superfície com a de outra figura tomada como unidade.

3. Por Exemplo: Para revestir uma parede com azulejos, Roberto precisou exatamente de 360 azulejos.Dizemos que a superfície da parede tem área de 360 unidades considerando a superfície de cada azulejo como unidade.

4. Unidade de Área Podemos assim, adotar como unidade de área um quadrado cujo lado mede uma unidade de comprimento. = 1 unidade de área1 Se o lado do quadrado for 1cm, por exemplo, a unidade de área será chamada de centímetro quadrado e representada por cm². Para cada unidade de comprimento, existe uma unidade de área correspondente.

5. Abaixo temos uma tabela com algumas unidades de área utilizadas quando forem convenientes para a figura que se deseja medir.

6. A área de uma figura exprime quantas vezes essa figura contém a unidade de área. Isso é fácil perceber, por exemplo, quando desejamos conhecer a área de um retângulo cujos lados medem 5cm e 3cm.3cm5cm

7. A unidade de área cabe 15 vezes no retângulo e, por isso, sua área é de 15 centímetros quadrados (15cm²).Fica evidente que se as medidas dos lados de um retângulo são números inteiros a e b, a sua área é o produto desses números:S = ab

8. EQUIVALÊNCIAS DE ÁREASDesenhamos uma região plana retangular, ABCD, com medidas de 5cm por 2cm. A partir de regiões planas como essa, usando recorte e colagens, obtivemos outras três, conforme as ilustrações abaixo.

10. Todas essas regiões planas têm uma característica comum: área de 10cm².

11. REFERÊNCIASDANTE, Luiz Roberto. Tudo é Matemática.7ª série. 2ªed. São Paulo: Ática, 2008. p. 220-221.ELON, L. Lima.; CARVALHO, P.C.P.; WAGNER E. e MORGADO, A.C. Temas e Problemas Elementares. 2ª ed. Rio de Janeiro: SBM, 2006. p. 86-87.