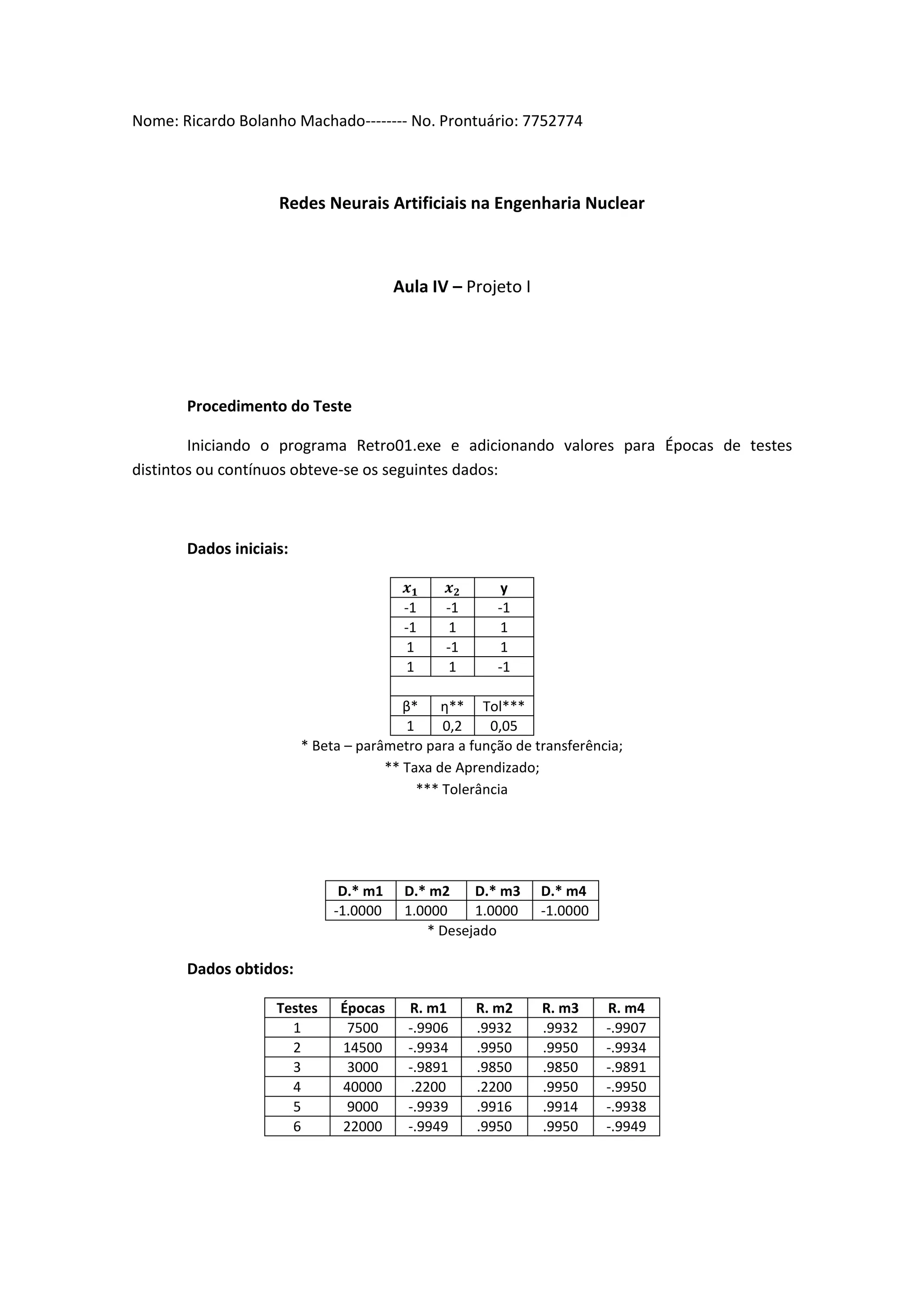
O documento descreve testes realizados em uma rede neural artificial treinada para reconhecer padrões de entrada. Os testes variaram o número de épocas de treinamento e analisaram como os pesos da rede e a função de erro convergiram com o treinamento. Conclui-se que quanto maior o número de épocas, mais os pesos se aproximaram dos valores desejados e a função de erro diminuiu, indicando que a rede aprendeu melhor os padrões.

1. Nome: Ricardo Bolanho Machado-------- No. Prontuário: 7752774
Redes Neurais Artificiais na Engenharia Nuclear
Aula IV – Projeto I
Procedimento do Teste
Iniciando o programa Retro01.exe e adicionando valores para Épocas de testes
distintos ou contínuos obteve-se os seguintes dados:
Dados iniciais:
-1
-1
1
1
-1
1
-1
1
y
-1
1
1
-1
β* η** Tol***
1
0,2
0,05
* Beta – parâmetro para a função de transferência;
** Taxa de Aprendizado;
*** Tolerância
D.* m1
-1.0000
D.* m2
D.* m3
1.0000
1.0000
* Desejado
D.* m4
-1.0000
R. m1
-.9906
-.9934
-.9891
.2200
-.9939
-.9949
R. m3
.9932
.9950
.9850
.9950
.9914
.9950
Dados obtidos:
Testes
1
2
3
4
5
6
Épocas
7500
14500
3000
40000
9000
22000
R. m2
.9932
.9950
.9850
.2200
.9916
.9950
R. m4
-.9907
-.9934
-.9891
-.9950
-.9938
-.9949

2. Analise da função energia do erro
No 1º teste, varia aproximadamente o erro da energia pela metade do valor
No 2º teste, varia aproximadamente 0,1E-005,variação ínfima, sendo que o valor inicial
já esta na potência de E-005.
No 3º teste, varia muito comparado o valor inicial fornecido ao neurônio artificial.
No 4º teste, varia pela metade do valor inicial.
No 5º teste, seu valor inicialmente se mantem decaindo vagarosamente e, de
repente,há uma queda maior e, posteriormente, volta a decair vagarosamente.
No 6º teste, cai lentamente do valor inicial para o valor final.
Conclusão
Pelos dados é possível notar que conforme aumenta o número de Épocas de
treinamento do neurônio os pesos foram alterados com variação convergindo para o mínimo
da função energia de erro, assim, aproximando-se cada vez mais do valor desejado.
Quanto a Épocas muito grandes a função energia de erro como analisado em 40000
Épocas decaiu muito do valor inicial, obtendo um valor absurdamente contraditório para dois
pesos, provando que para Épocas muito grandes a rede obteve êxito na aprendizagem
atingindo o mínimo global, já que para valores próximos de 22000 a rede esteve próximo do
valor desejado para os pesos e a função energia de erro teve menores variações.
No entanto, não inclui muitos dados, pois conforme fui treinando a rede ela
aparentemente correspondeu à análise dos dados acima, sendo que acabei me esquecendo de
anotar alguns deles, mas eram testes separados e não achei necessidade de refazer mais, já
que conclui minha análise e aparentemente a rede me fornecia dados parecidos.