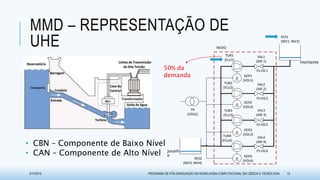
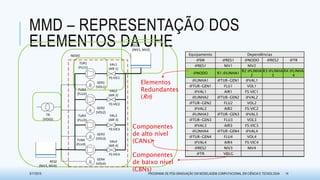
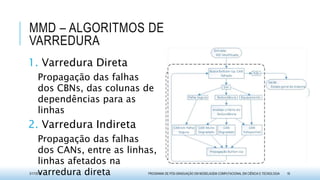
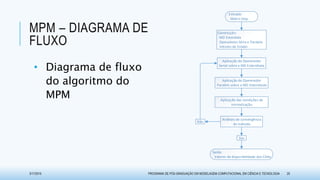
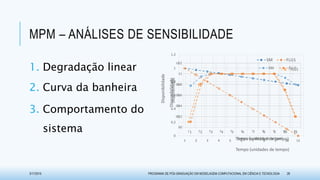
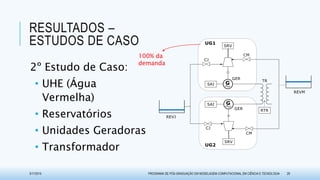
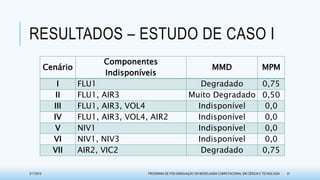
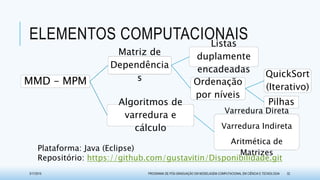
O documento discute métodos para avaliar a disponibilidade em sistemas de usinas hidrelétricas na geração de energia. Ele propõe duas técnicas baseadas em matrizes de dependências: o Método de Matriz de Dependências (MMD), que usa uma abordagem qualitativa, e o Método de Propagação de Markov (MPM), que adota uma abordagem quantitativa. O documento também apresenta exemplos de aplicação dessas metodologias e resultados obtidos na pesquisa.

























![COMPARAÇÃO DAS
METODOLOGIAS
Aspectos avaliados MMD MPM
Tipo de Abordagem Qualitativa Quantitativa
Espaço de estados Escala de cores (5
níveis)
Intervalo: [0,
1]
Uso de matrizes de
dependências
Sim Sim
Variabilidade da
disponibilidade dos
CBNs
Não Sim
Informação de Necessária Necessária3/17/2015 PROGRAMA DE PÓS-GRADUAÇÃO EM MODELAGEM COMPUTACIONAL EM CIÊNCIA E TECNOLOGIA 34](https://image.slidesharecdn.com/beeb117f-818b-4c5f-9fe4-46c48a19842e-150317071952-conversion-gate01/85/Presentacao-34-320.jpg)





