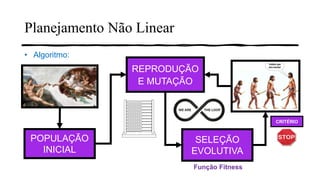
1) O documento discute planejamento não linear e apresenta exemplos de como algoritmos genéticos e sistemas de equações diferenciais não lineares podem ser usados para planejamento de produção.
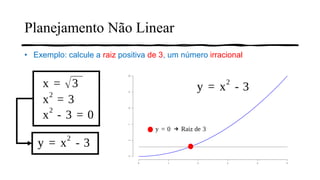
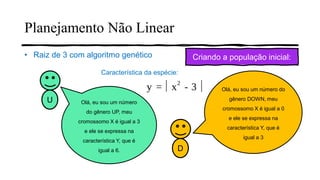
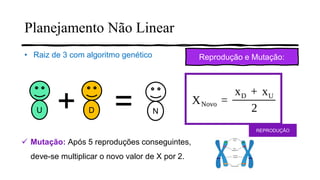
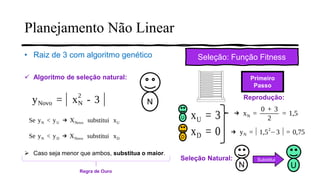
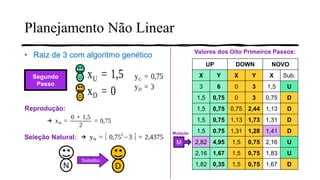
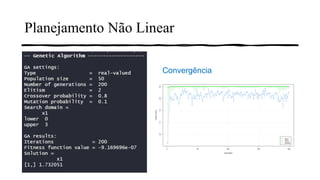
2) É apresentado um exemplo passo-a-passo de como um algoritmo genético pode ser usado para encontrar a raiz quadrada de 3.
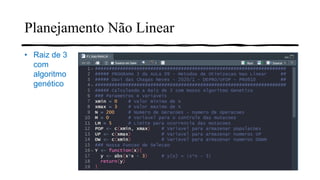
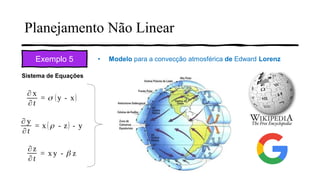
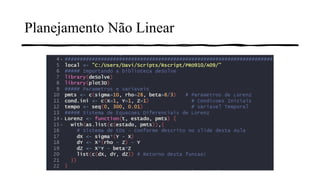
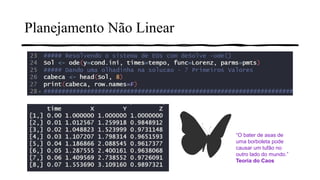
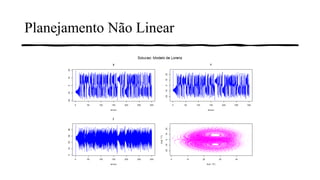
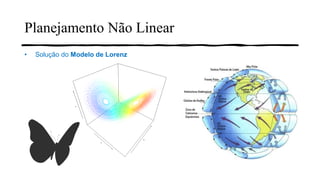
3) Também é mostrado como o pacote R deSolve pode resolver sistemas de equações diferenciais não lineares, como o modelo de Lorenz.