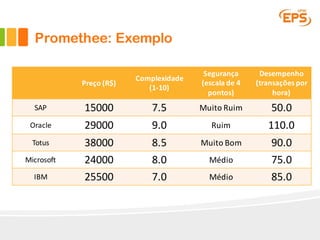
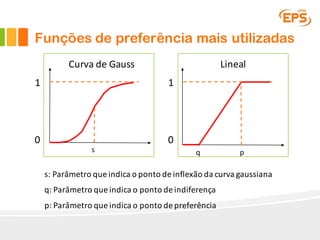
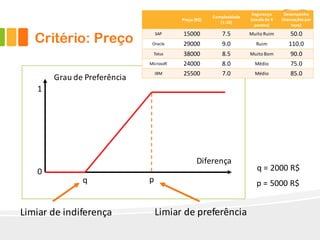
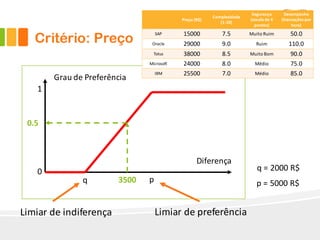
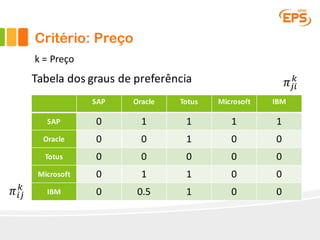
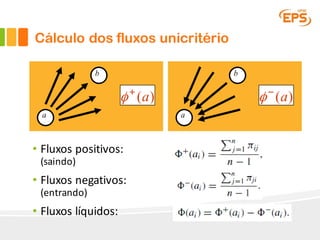
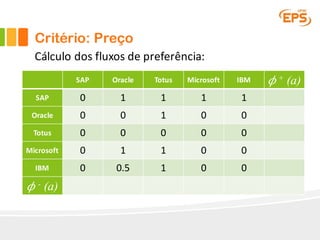
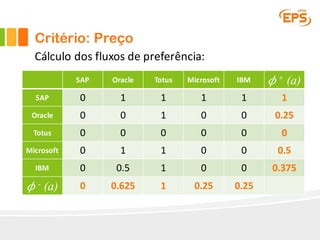
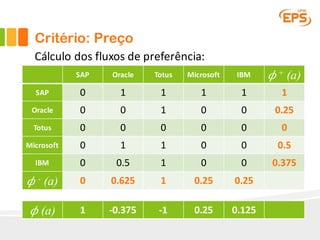
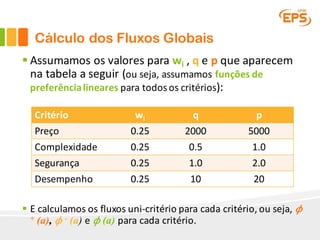
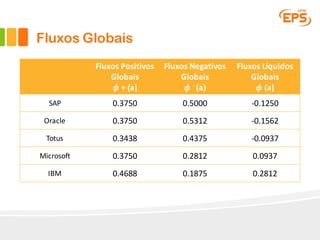
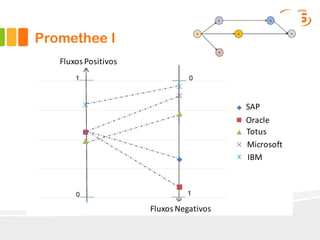
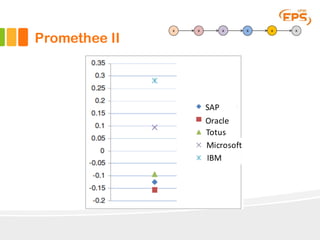
O documento descreve o método Promethee para tomada de decisão multicritério. O método envolve três etapas: 1) cálculo dos graus de preferência entre pares de alternativas para cada critério, 2) cálculo dos fluxos uni-critério, e 3) cálculo dos fluxos globais a partir dos fluxos uni-critério e pesos dos critérios. O método gera rankings das alternativas com base nos fluxos positivos, negativos e líquidos globais.

1. Prof. Dr. Mauricio Uriona Maldonado
EPS 7009 – Teoria da Decisão
Departamentode Engenharia de Produçãoe Sistemas
Métodos outranking
Método Promethee

2. Métodos de
agregação
Métodos
Outranking
Sistemas de
Apoio à
Decisão
MAUT, Soma
Ponderada,
Produto Ponderado,
Topsis, AHP
Família de
Métodos
Electre,
Promethée
Dinâmica
de
Sistemas

3. Introdução
§ Os métodos outranking apresentam a
noção das alternativas não serem
necessariamente comparáveis;
§ Isto se dá pelo fato de existirem três tipos
de resultados, com relação à
comparação: preferência, indiferença e
incomparabilidade.

4. Introdução
1. Preferência: aPb ou bPa
2. Indiferença: aIb
3. Incomparabilidade: aRb
§ Ou seja, existem agora três formas de
comparar as alternativas a e b:
§ P, I e R: definem a estrutura de preferências
se, para todo a,b de A, uma e apenas uma das
opções acima é válida.

5. Introdução
§ Desta forma, em muitas situações, duas
alternativas não podem ser comparadas
entre si;
§ Portanto, não é mais possível estabelecer
uma ordem de preferência (no sentido do
axioma da transitividade);
§ Assim, torna-se necessário redefinir o
conceito de decisão:

6. Introdução
§ Seleção: de um conjunto de alternativas é
selecionado um pequeno subconjunto de
alternativas consideradas como “melhores”;
§ Classificação: cada alternativa é agrupada em
uma classe onde não existe ordem entre
classes;
§ Ordenação: as alternativas ou parte delas, são
levadas a uma ordem de preferência (total ou
parcial).

7. § O método Promethee (Preference Ranking
Organization Method for Enriched Evaluation)
oferece um ranking com base em graus de
preferência;
§ Três passos/etapas:
§ Cálculo dos graus de preferência para cada par de
ações de cada critério;
§ Cálculo dos fluxos uni-critério;
§ Cálculo dos fluxos globais.
Promethee

8. Promethee: Exemplo
§ Decisão: escolher um ERP dentre cinco diferentes
opções;
§ Quatro critérios são definidos:
§ Preço (a ser minimizado);
§ Complexidade(a ser minimizado);
§ Segurança (a ser maximizado); e
§ Desempenho (a ser maximizado)
§ Da tabela a seguir, observa-se que não existe uma
opção ‘ideal’, ou seja, existem trade-offs entre as
opções

9. Preço (R$)
Complexidade
(1-10)
Segurança
(escala de 4
pontos)
Desempenho
(transações por
hora)
SAP 15000 7.5 Muito Ruim 50.0
Oracle 29000 9.0 Ruim 110.0
Totus 38000 8.5 Muito Bom 90.0
Microsoft 24000 8.0 Médio 75.0
IBM 25500 7.0 Médio 85.0
Promethee: Exemplo

10. Promethee: Exemplo
§ O primeiro passo/etapa é calcular o grau de
preferência do tomador de decisão, para cada um dos
critérios identificados (neste caso, quatro);
§ Isto é feito a partir da identificação da função de
preferência (similar a função utilidade da teoria de decisão sob risco)
para cada critério;
§ Para fins de facilitar essa identificação, são utilizadas
funções gráficas;
§ A função de preferência indica a preferência do
tomador de decisão com relação a duas alternativas.

11. q p
0
1
Curva de Gauss
s
Funções de preferência mais utilizadas
Lineal
0
1
s: Parâmetro que indica o ponto de inflexão da curva gaussiana
q: Parâmetro que indica o ponto de indiferença
p: Parâmetro que indica o ponto de preferência

12. Forma Usual
Outras funções de preferência
0
1
Forma U
0
1
0
1
0
1
p
q
q p
Forma V Forma em Níveis
q=p=0
p=0
q=0

13. Promethee: Exemplo
§ Para cada critério:
§ utiliza-se uma das funções previamente apresentadas,
com ela são realizadas as comparações entre as
alternativas ‘par a par’.
§ O resultado dessa comparação é levado a uma tabela
de comparações (similar àquela do método AHP);
§ A seguir, apresenta-se o passo a passo das
comparações para o primeiro critério (preço),
assumindo uma função de preferência linear, com
q=2000 R$ e p=5000 R$.

14. q p
0
1
Limiar de indiferença Limiar de preferência
Grau de Preferência
Diferença
Critério: Preço
q = 2000 R$
p = 5000 R$
Preço (R$)
Complexidade
(1-10)
Segurança
(escala de 4
pontos)
Desempenho
(transações por
hora)
SAP 15000 7.5 Muito Ruim 50.0
Oracle 29000 9.0 Ruim 110.0
Totus 38000 8.5 Muito Bom 90.0
Microsoft 24000 8.0 Médio 75.0
IBM 25500 7.0 Médio 85.0

15. q p
0
1
Grau de Preferência
Diferença
3500
0.5
Critério: Preço
q = 2000 R$
p = 5000 R$
Preço (R$)
Complexidade
(1-10)
Segurança
(escala de 4
pontos)
Desempenho
(transações por
hora)
SAP 15000 7.5 Muito Ruim 50.0
Oracle 29000 9.0 Ruim 110.0
Totus 38000 8.5 Muito Bom 90.0
Microsoft 24000 8.0 Médio 75.0
IBM 25500 7.0 Médio 85.0
Limiar de indiferença Limiar de preferência

16. Para o cálculo dos graus de preferência
Se
Se
Se
§ Para funções lineares:
𝜋"#
$

17. Para o cálculo dos graus de preferência
Se
De outra forma
§ Para funções gaussianas:
𝜋"#
$

18. Critério: Preço
SAP Oracle Totus Microsoft IBM
SAP 0 1 1 1 1
Oracle 0 0 1 0 0
Totus 0 0 0 0 0
Microsoft 0 1 1 0 0
IBM 0 0.5 1 0 0
Tabela dos graus de preferência
k = Preço
𝜋"#
$
𝜋#"
$

19. Critério: Preço
§ O segundo passo é o cálculo dos fluxos unicritério:
fluxos positivos, fluxos negativos e fluxos líquidos;
§ Fluxos positivos (fluxos saindo): nota de 0 a 1, indica o grau
de preferência de uma alternativa sobre todas as outras (por
filas);
§ Fluxos negativos (fluxos entrando): nota de 0 a 1, indica o
grau de preferência de todas as outras (por colunas);
§ Fluxos líquidos: soma dos fluxos positivos e negativos por
alternativa.

20. • Fluxos positivos:
(saindo)
• Fluxos negativos:
(entrando)
• Fluxos líquidos:
a
b
( )aφ+
a
b
( )aφ−
Cálculo dos fluxos unicritério

21. Critério: Preço
SAP Oracle Totus Microsoft IBM 𝜙 + (a)
SAP 0 1 1 1 1
Oracle 0 0 1 0 0
Totus 0 0 0 0 0
Microsoft 0 1 1 0 0
IBM 0 0.5 1 0 0
𝜙 - (a)
Cálculo dos fluxos de preferência:

22. Critério: Preço
SAP Oracle Totus Microsoft IBM 𝜙 + (a)
SAP 0 1 1 1 1 1
Oracle 0 0 1 0 0 0.25
Totus 0 0 0 0 0 0
Microsoft 0 1 1 0 0 0.5
IBM 0 0.5 1 0 0 0.375
𝜙 - (a) 0 0.625 1 0.25 0.25
Cálculo dos fluxos de preferência:

23. Critério: Preço
SAP Oracle Totus Microsoft IBM 𝜙 + (a)
SAP 0 1 1 1 1 1
Oracle 0 0 1 0 0 0.25
Totus 0 0 0 0 0 0
Microsoft 0 1 1 0 0 0.5
IBM 0 0.5 1 0 0 0.375
𝜙 - (a) 0 0.625 1 0.25 0.25
Cálculo dos fluxos de preferência:
𝜙 (a) 1 -0.375 -1 0.25 0.125

24. Cálculo dos Fluxos Globais
§ O terceiro passo é o cálculo dos fluxos globais, a partir
do fluxos uni-critério (calculados anteriormente)
§ Obs.: o procedimento apresentado anteriormente para o
critério ‘preço’, deve ser reproduzido para cada um dos
critérios restantes;
§ Assim, teremos 𝜙 + (a), 𝜙 - (a) e 𝜙 (a) para cada um
dos quatro critérios do nosso problema;
§ Adicionalmente, para o cálculo dos fluxos globais,
precisamos também dos ‘peso relativo’ de cada
critério.

25. Critério wi q p
Preço 0.25 2000 5000
Complexidade 0.25 0.5 1.0
Segurança 0.25 1.0 2.0
Desempenho 0.25 10 20
Cálculo dos Fluxos Globais
§ Assumamos os valores para wi , q e p que aparecem
na tabela a seguir (ou seja, assumamos funções de
preferência lineares para todos os critérios):
§ E calculamos os fluxos uni-critério para cada critério, ou seja, 𝜙
+ (a), 𝜙 - (a) e 𝜙 (a) para cada critério.

26. § Por fim, realiza-se uma soma ponderada de cada
fluxo uni-critério do critério i, multiplicado pelo peso
relativo do critério i;
§ Utiliza-se a equação:
ϕ a = ∑ wi
k
i=1 ∗ϕi a
Cálculo dos Fluxos Globais
§ Os fluxos globais, aparecem na tabela a seguir.

27. Fluxos Positivos
Globais
𝜙 + (a)
Fluxos Negativos
Globais
𝜙 - (a)
Fluxos Líquidos
Globais
𝜙 (a)
SAP 0.3750 0.5000 -0.1250
Oracle 0.3750 0.5312 -0.1562
Totus 0.3438 0.4375 -0.0937
Microsoft 0.3750 0.2812 0.0937
IBM 0.4688 0.1875 0.2812
Fluxos Globais

28. E a escolha?
§ A escolha da melhor opção de compra pode ser obtida
de duas formas:
§ A partir dos rankings dos fluxos positivos e negativos globais
(procedimento conhecido como Promethee I); e
§ A partir dos rankings dos fluxos líquidos globais
(procedimento conhecido como Promethee II).
§ Promethee I oferece um rankeamento ‘parcial’ no
sentido de representar o estado da incomparabilidade;
§ Promethee II oferece um rankeamento ‘total’, onde o
estado da incomparabilidade não existe.

29. Promethee I
Fluxos Positivos
Fluxos Negativos
SAP
Oracle
Microsoft
Totus
IBM

30. Promethee II
SAP
Oracle
Microsoft
Totus
IBM

31. Bibliografia
1. Ishizaka, A. et al (2013). Multi Criteria Decision
Analysis: Methods and Software. Cap 6. Promethee.
This work is licensed under a Creative Commons Attribution-
NonCommercial-ShareAlike 4.0 International License.

32. EPS 7009 – Teoria da Decisão
Departamentode Engenharia de Produçãoe Sistemas
Prof. Dr. Mauricio Uriona Maldonado
Métodos outranking
Métodos Promethee