Transferir como PDF, PPTX
Carregado porMauricio Uriona Maldonado PhD
AHP - Analytic Hierarchy Process
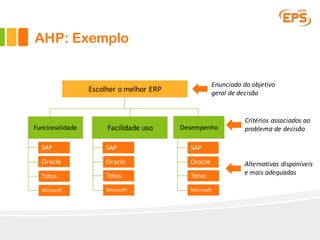
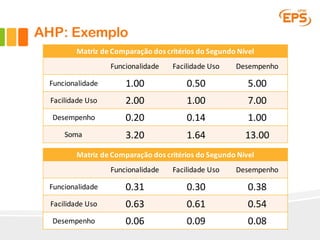
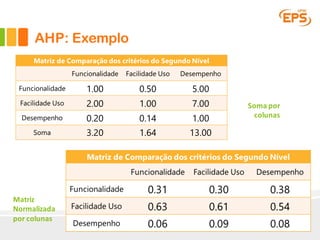
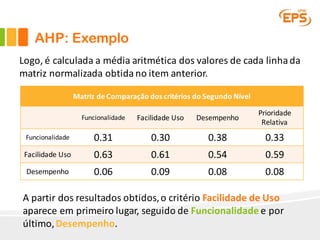
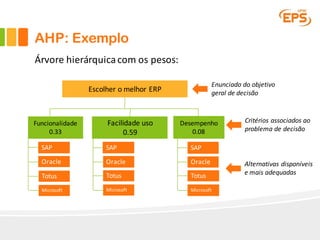
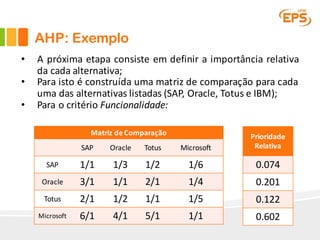
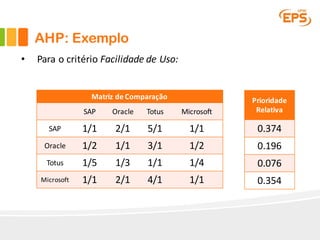
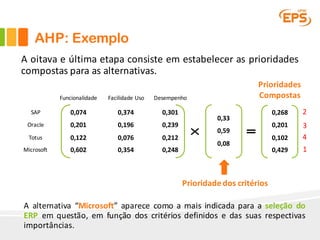
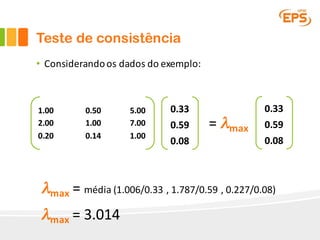
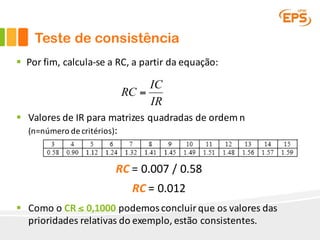
O documento descreve o Método AHP (Analytic Hierarchy Process), um método multicritério para tomada de decisão. O AHP permite a avaliação de alternativas considerando critérios qualitativos e quantitativos de forma hierárquica. É apresentado um exemplo passo a passo ilustrando como o método pode ser aplicado para escolher entre fornecedores de software ERP considerando funcionalidade, facilidade de uso e desempenho.
AHP - Analytic Hierarchy Process
- 1. Prof. Dr. MauricioUriona Maldonado EPS 7009 – Teoria da Decisão Departamentode Engenharia de Produçãoe Sistemas Método AHP
- 2.
- 3. AHP (Analytic HierarchyProcess) § Um dos métodos multicritério mais utilizados; § Criado pelo Professor Thomas L. Saaty em 1980; § Permite o uso de critérios qualitativos bem como quantitativos no processo de avaliação. § A ideia principal é dividir o problema de decisão em níveis hierárquicos, facilitando, assim, sua compreensão e avaliação.
- 4. SELEÇÃO DE SOFTWARE ERP § Funcionalidade; § Facilidade de uso; §Desempenho; § Escalabilidade; § Etc. AHP: Exemplo
- 5. AHP: Exemplo 1. Vamos assumir que a empresa optou por comprar o ERP de fornecedores no mercado, ao invés de desenvolver o sistema internamente; 2.A empresa identificou quatro fornecedores: SAP, Oracle, Totus e Microsoft Dynamics; 3. Para realizar a escolha do melhor fornecedor, a gerência de TI exige que seja levantado um estudo comparativo, a partir do qual são identificados os critérios de funcionalidade, facilidade de uso, e desempenho. 4. Qual fornecedor escolher?
- 6. Passos: 1. Definir oobjetivo; 2. Definir os critérios de priorização; 3. Definir as alternativas; 4. Definir a importância relativa de cada critério (par a par); 5. Definir a importância relativa de cada alternativa (par a par); 6. Normalizar as tabelas de comparação; 7. Calcular os auto-vetores; 8. Definir as prioridades de cada alternativa. AHP: Exemplo
- 7.
- 8. • A próximaetapa consiste em estabelecer prioridades entre os elementos para cada nível da hierarquia, por meio de uma matriz de comparação. • O primeiro ponto a ser considerado é a determinação de uma escala de valores para comparação, que não deve exceder um total de nove fatores, a fim de se manter a matriz consistente. • Assim, utiliza-se uma escala fundamental. AHP: Exemplo
- 9. Escala Fundamental do Método AHP 1 Igual importância As duas atividades contribuem igualmente para o objetivo 3Importância pequena de uma sobre a outra A experiência e o juízo favorecem uma atividade em relação à outra 5 Importância grande ou essencial A experiência ou juízo favorece fortemente uma atividade em relação à outra 7 Importância muito grande ou demonstrada Uma atividade é muito fortemente favorecida em relação à outra. Pode ser demonstrada na prática. 9 Importância absoluta A evidencia favorece uma atividade em relação à outra, com o mais alto grau de segurança. 2, 4, 6, 8 Valores Intermediários Quando se procura uma condição de compromisso entre duas definições AHP: Exemplo
- 10. § Facilidade de uso é 2/1 – ligeiramente mais importante –que funcionalidade; § Funcionalidade é 5/1 – mais importante – Desempenho; § Facilidade de uso é 7/1 – muito mais importante – que Desempenho. Considerando os 3 critérios da estrutura hierárquica, foram desenvolvidas a seguintes comparações “par a par”: AHP: Exemplo
- 11. Considerando os 3critérios da estrutura hierárquica (exemplo) foi desenvolvida a seguinte matriz de comparação quadrada. Matriz de Comparação dos critérios do Segundo Nível Funcionalidade Facilidade Uso Desempenho Funcionalidade 1/1 1/2 5/1 Facilidade Uso 2/1 1/1 7/1 Desempenho 1/5 1/7 1/1 AHP: Exemplo
- 12. • A Matriz anterior deve ser “normalizada” utilizando procedimentos matemáticos à autovetor; •O resultado da normalização = priorização dos critérios; • Contudo, existe um método “aproximado” para calcular a matriz normalizada. AHP: Exemplo
- 13. Matriz de Comparação dos critérios do Segundo Nível Funcionalidade Facilidade Uso Desempenho Funcionalidade1.00 0.50 5.00 Facilidade Uso 2.00 1.00 7.00 Desempenho 0.20 0.14 1.00 Soma 3.20 1.64 13.00 Matriz de Comparação dos critérios do Segundo Nível Funcionalidade Facilidade Uso Desempenho Funcionalidade 0.31 0.30 0.38 Facilidade Uso 0.63 0.61 0.54 Desempenho 0.06 0.09 0.08 AHP: Exemplo
- 14.
- 15. Matriz de Comparação dos critérios do Segundo Nível Funcionalidade Facilidade Uso Desempenho Prioridade Relativa Funcionalidade0.31 0.30 0.38 0.33 Facilidade Uso 0.63 0.61 0.54 0.59 Desempenho 0.06 0.09 0.08 0.08 Logo, é calculada a média aritmética dos valores de cada linha da matriz normalizada obtida no item anterior. A partir dos resultados obtidos, o critério Facilidade de Uso aparece em primeiro lugar, seguido de Funcionalidade e por último, Desempenho. AHP: Exemplo
- 16. Desta forma, obtêm-se a matriz de comparação A e o vetor de prioridades w: AHP: Exemplo 1.00 0.505.00 2.00 1.00 7.00 0.20 0.14 1.00 1.00 0.50 5.00 0,33 0,59 0,08 A = w =
- 17.
- 18. • A próximaetapa consiste em definir a importância relativa da cada alternativa; • Para isto é construída uma matriz de comparação para cada uma das alternativas listadas (SAP, Oracle, Totus e IBM); • Para o critério Funcionalidade: Matriz de Comparação SAP Oracle Totus Microsoft SAP 1/1 1/3 1/2 1/6 Oracle 3/1 1/1 2/1 1/4 Totus 2/1 1/2 1/1 1/5 Microsoft 6/1 4/1 5/1 1/1 Prioridade Relativa 0.074 0.201 0.122 0.602 AHP: Exemplo
- 19. • Para ocritério Facilidade de Uso: Matriz de Comparação SAP Oracle Totus Microsoft SAP 1/1 2/1 5/1 1/1 Oracle 1/2 1/1 3/1 1/2 Totus 1/5 1/3 1/1 1/4 Microsoft 1/1 2/1 4/1 1/1 Prioridade Relativa 0.374 0.196 0.076 0.354 AHP: Exemplo
- 20. • Para ocritério Desempenho, podemos utilizar uma escala numérica, por exemplo, relacionado com algum indicador de processamento de transações por unidade de tempo: TP/hora Normalizado SAP 34 0.301 Oracle 27 0.239 Totus 24 0.212 Microsoft 28 0.248 113 AHP: Exemplo
- 21. A oitava eúltima etapa consiste em estabelecer as prioridades compostas para as alternativas. Funcionalidade Facilidade Uso Desempenho SAP 0,074 0,374 0,301 Oracle 0,201 0,196 0,239 Totus 0,122 0,076 0,212 Microsoft 0,602 0,354 0,248 × 0,33 0,59 0,08 = Prioridade dos critérios 0,268 0,201 0,102 0,429 Prioridades Compostas A alternativa “Microsoft” aparece como a mais indicada para a seleção do ERP em questão, em função dos critérios definidos e das suas respectivas importâncias. 1 2 3 4 AHP: Exemplo
- 22. Teste de consistência §As avaliações do método AHP são baseadas no pressuposto de que o decisor é racional, isto é, se A é preferido a B e B é preferível a C, então A é preferido a C (axioma da transitividade) § Deve-se, portanto, testar a consistência das comparações (par a par). § Para isto, calcula-se a Razão de Consistência (RC), que serve para medir o quanto os julgamentos foram consistentes em relação a grandes amostras de juízos completamente aleatórios; § Assim, é necessário primeiro obter o valor de λmax que representa o maior autovalor da matriz A,obtido a partir da seguinte equação: wAw ×= maxλ
- 23. • Considerandoos dados do exemplo: Testede consistência 1.00 0.50 5.00 2.00 1.00 7.00 0.20 0.14 1.00 0.33 0.59 0.08 = λmax 0.33 0.59 0.08 λmax = média (1.006/0.33 , 1.787/0.59 , 0.227/0.08) λmax = 3.014
- 24. Teste de consistência §Uma vez calculado o λmax , deve-se calcular o Índice de Consistência (IC) para logo calcular a Razão de Consistência (RC). § O índice de consistência é determinado de acordo com a fórmula abaixo, em que n é o número de critérios: 1− − = n n IC maxλ IC = (3.014 – 3) / (3 – 1) IC = 0.007
- 25. Teste de consistência §Por fim, calcula-se a RC, a partir da equação: 01580 580 00910 , , , === IR IC RC § Valores de IR para matrizes quadradas de ordem n (n=número de critérios): RC = 0.007 / 0.58 RC = 0.012 § Como o CR ≤ 0,1000 podemos concluir que os valores das prioridades relativas do exemplo, estão consistentes.
- 26. Bibliografia 1. Ishizaka, A.et al (2013). Multi Criteria Decision Analysis: Methods and Software. Cap 2. Analytic Hierarchy Process. 2. Ragsdale, Cliff T. (2015). Modelagem de Planilha e Análise de Decisão: Uma introdução prática a business analytics. Cengage Learning. 616p. Cap. 14. Análise de Decisão.
- 27. Bibliografia 3. Taylor, B.W. (2013). Introduction to management science. Prentice Hall. Cap 9. Multicriteria decision making. Pp.422-476. This work is licensed under a Creative Commons Attribution- NonCommercial-ShareAlike 4.0 International License.
- 28. EPS 7009 –Teoria da Decisão Departamentode Engenharia de Produçãoe Sistemas Método AHP Prof. Dr. Mauricio Uriona Maldonado