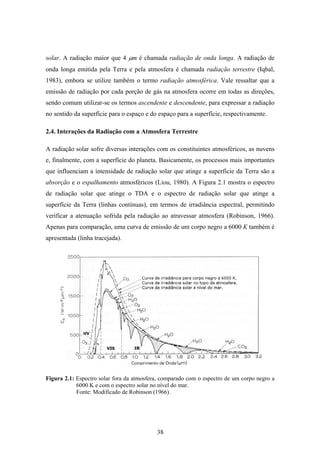
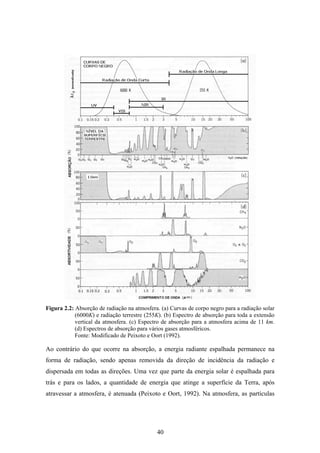
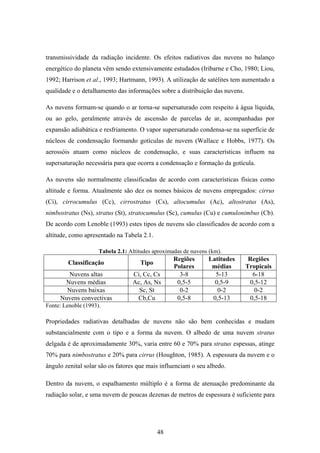
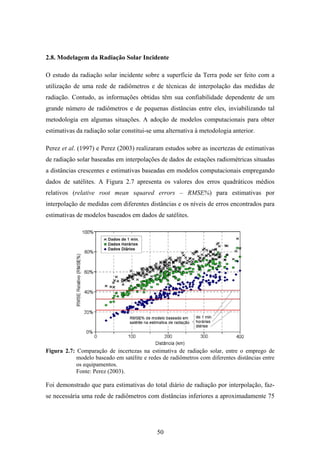
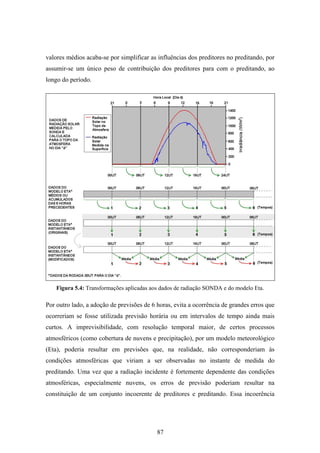
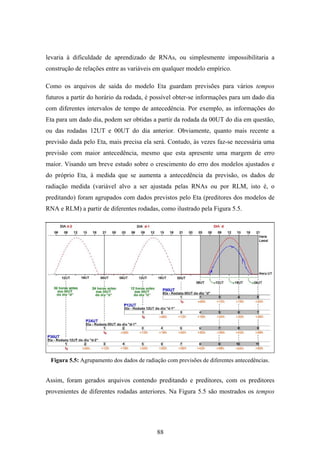
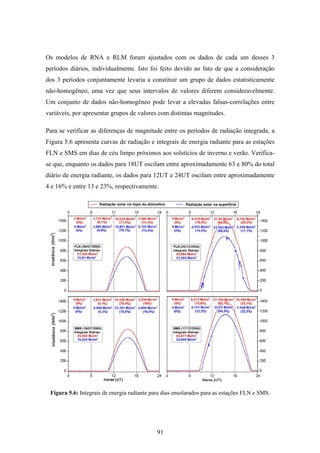
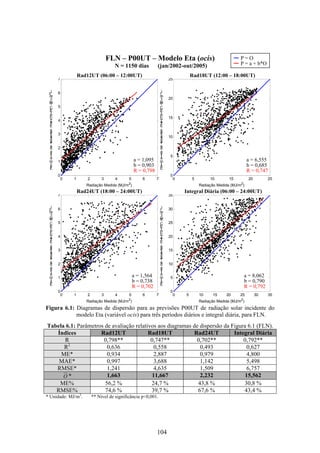
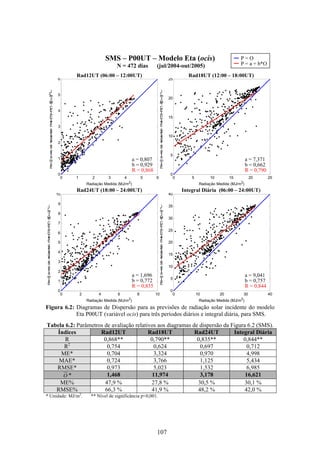
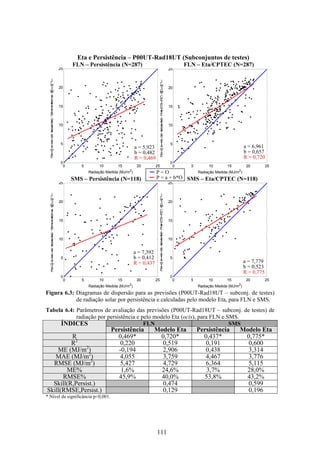
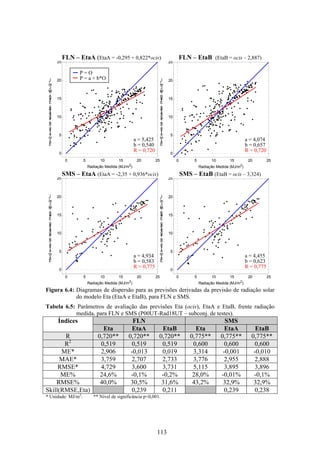
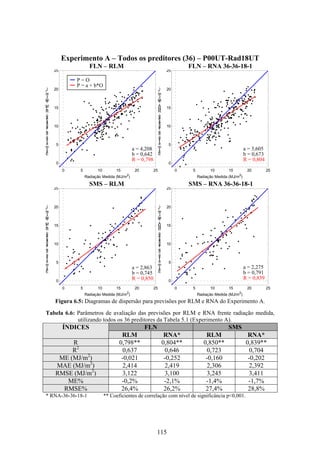
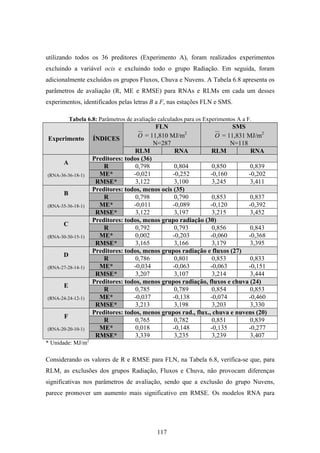
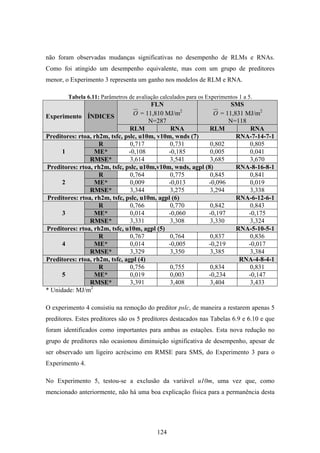
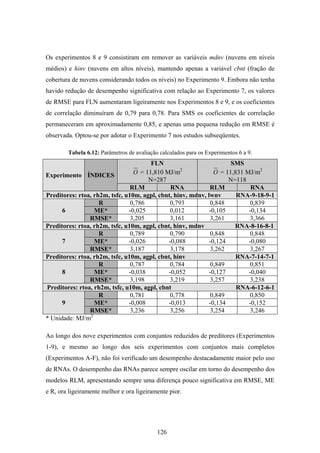
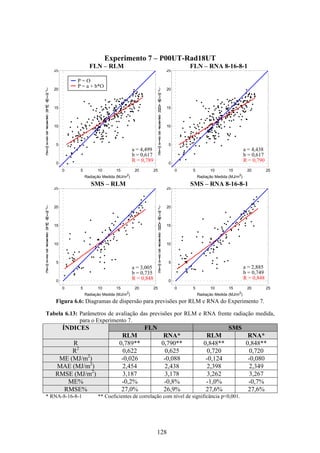
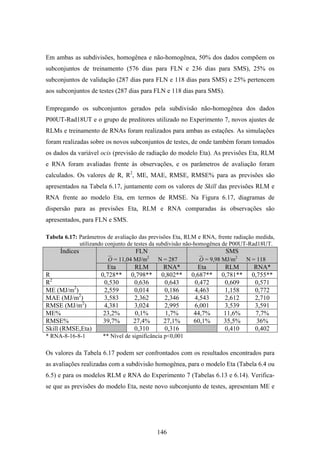
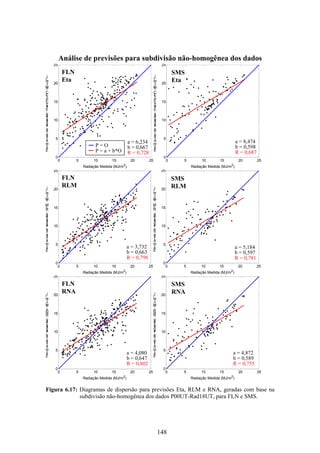
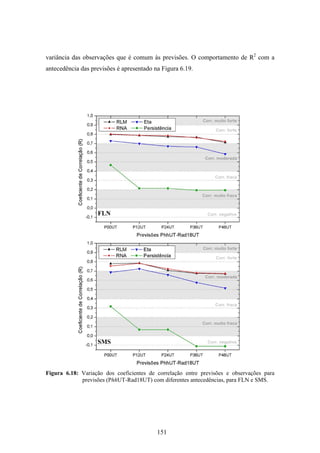
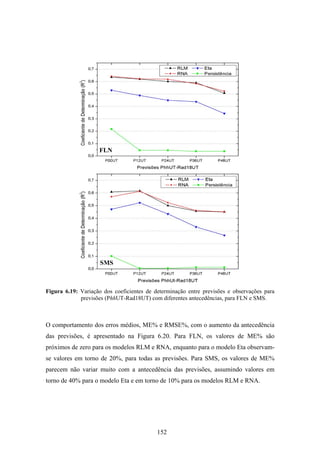
1. O documento descreve uma pesquisa que teve como objetivo desenvolver e avaliar uma metodologia para refinar as previsões de radiação solar produzidas pelo modelo Eta/CPTEC. Foram utilizadas redes neurais artificiais e regressões lineares múltiplas para calcular a radiação solar incidente em duas estações, utilizando variáveis de saída do modelo Eta como preditores.
2. Dados de radiação solar medidos nas estações foram usados para seleção de preditores, treinamento dos modelos e avaliação das