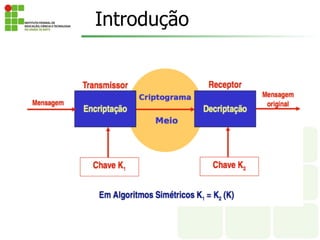
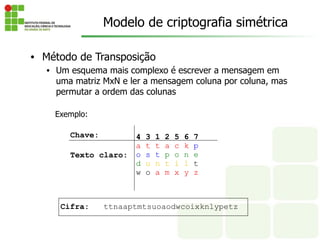
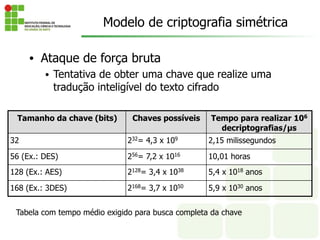
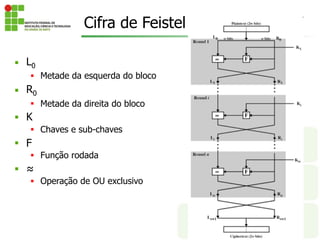
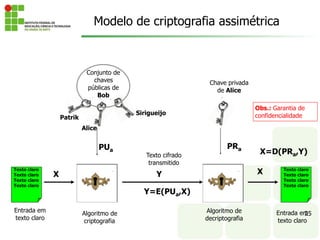
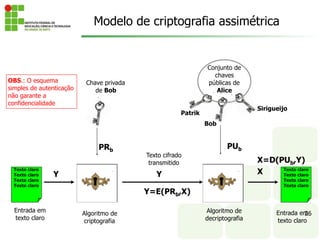
O documento discute os conceitos fundamentais de criptografia, incluindo criptografia simétrica e assimétrica. Ele explica que a criptografia simétrica usa uma única chave para criptografar e descriptografar, enquanto a criptografia assimétrica usa chaves públicas e privadas. O documento também descreve vários algoritmos criptográficos, como DES, 3DES e AES.