ANÁLISE DE COMPORTAMENTO NÃO COOPERATIVO EM COMPUTAÇÃO VOLUNTÁRIA

UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL
INSTITUTO DE INFORMÁTICA
PROGRAMA DE PÓS-GRADUAÇÃO EM COMPUTAÇÃO
BRUNO LUIS DE MOURA DONASSOLO
Análise do Comportamento Não
Cooperativo em Computação Voluntária
Dissertação apresentada como requisito parcial
para a obtenção do grau de
Mestre em Ciência da Computação
Prof. Dr. Cláudio Geyer
Orientador
Prof. Dr. Arnaud Legrand
Co-orientador
Porto Alegre, agosto de 2011

CIP – CATALOGAÇÃO NA PUBLICAÇÃO
de Moura Donassolo, Bruno Luis
Análise do Comportamento Não Cooperativo em Computa-
ção Voluntária / Bruno Luis de Moura Donassolo. – Porto Alegre:
PPGC da UFRGS, 2011.
93 f.: il.
Dissertação (mestrado) – Universidade Federal do Rio Grande
do Sul. Programa de Pós-Graduação em Computação, Porto Ale-
gre, BR–RS, 2011. Orientador: Cláudio Geyer; Co-orientador:
Arnaud Legrand.
1. Computação voluntária. 2. Teoria dos jogos. 3. Escalona-
mento. 4. Simulação. 5. BOINC. 6. Simgrid. I. Geyer, Cláudio.
II. Legrand, Arnaud. III. Título.
UNIVERSIDADE FEDERAL DO RIO GRANDE DO SUL
Reitor: Prof. Carlos Alexandre Netto
Vice-Reitor: Prof. Rui Vicente Oppermann
Pró-Reitora de Pós-Graduação: Prof. Aldo Bolten Lucion
Diretor do Instituto de Informática: Prof. Flávio Rech Wagner
Coordenador do PPGC: Prof. Álvaro Freitas Moreira
Bibliotecária-chefe do Instituto de Informática: Beatriz Regina Bastos Haro

SUMÁRIO
LISTA DE ABREVIATURAS E SIGLAS . . . . . . . . . . . . . . . . . . . . 5
LISTA DE FIGURAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 7
LISTA DE TABELAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9
RESUMO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11
ABSTRACT . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 13
1 INTRODUÇÃO . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 15
2 TRABALHOS RELACIONADOS . . . . . . . . . . . . . . . . . . . . . 19
2.1 Computação Voluntária . . . . . . . . . . . . . . . . . . . . . . . . . . . 19
2.2 BOINC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.2.1 Cliente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
2.2.2 Servidor . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.3 Simulação . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
2.3.1 Simuladores específicos do BOINC . . . . . . . . . . . . . . . . . . . . . 26
2.3.2 Simuladores de propósito geral . . . . . . . . . . . . . . . . . . . . . . . 27
2.4 Considerações Finais . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
3 SIMULADOR DO BOINC . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.1 Introdução . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 29
3.2 SimGrid . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31
3.2.1 Núcleo de simulação . . . . . . . . . . . . . . . . . . . . . . . . . . . . 32
3.2.2 Análise de um simples caso de Computação Voluntária . . . . . . . . . . 36
3.2.3 Melhorias propostas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 38
3.2.4 Avaliação de desempenho . . . . . . . . . . . . . . . . . . . . . . . . . . 40
3.3 Simulador do BOINC proposto . . . . . . . . . . . . . . . . . . . . . . . 44
3.3.1 Validação . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46
4 NOTAÇÃO TEÓRICA DO JOGO . . . . . . . . . . . . . . . . . . . . . . 49
5 ESTUDO EXPERIMENTAL . . . . . . . . . . . . . . . . . . . . . . . . . 55
5.1 Definição da configuração . . . . . . . . . . . . . . . . . . . . . . . . . . 55
5.2 Otimização e influência dos parâmetros dos projetos . . . . . . . . . . . 56
5.2.1 Influência do deadline e do intervalo de conexão . . . . . . . . . . . . . . 56
5.2.2 Influência das estratégias de escalonamento . . . . . . . . . . . . . . . . 56

5.2.3 Réplicas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59
5.3 Influência dos projetos em rajadas nos projetos contínuos . . . . . . . . 62
5.3.1 Influência do tamanho da rajada . . . . . . . . . . . . . . . . . . . . . . 62
5.3.2 Influência do número de projetos em rajadas . . . . . . . . . . . . . . . . 63
5.4 Equilíbrio de Nash e amostras do conjunto de utilidade . . . . . . . . . 64
5.4.1 Estratégia da melhor resposta . . . . . . . . . . . . . . . . . . . . . . . . 64
6 CONCLUSÃO E TRABALHOS FUTUROS . . . . . . . . . . . . . . . . 71
REFERÊNCIAS . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 75
APÊNDICE A
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
A.1 Influência do deadline e intervalo de conexão com réplicas . . . . . . . . 81
A.1.1 Fixa . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
A.1.2 Saturação . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 81
A.1.3 EDF . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 82
APÊNDICE B
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
B.1 Equilíbrios de Nash com diferentes números de clientes . . . . . . . . . 87
B.1.1 100 Clientes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 87
B.1.2 500 Clientes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89
B.1.3 2000 Clientes . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 89

LISTA DE ABREVIATURAS E SIGLAS
API Application Programming Interface
BOINC Berkley Open Infrastructure for Networking Computing
CE Cluster Equivalence
CPU Central Processing Unit
CV Computação Voluntária
DAG Directed Acyclic Graph
EDF Earliest Deadline First
FLOPS Floating Point Operations per Second
GRAS Grid Reality And Simulation
GPU Graphics Processing Unit
LAN Local Area Network
MPI Message Passing Interface
NAT Network Address Translation
NE Nash Equilibrium
OS Operating System
RAM Random Access Memory
TCP Transmission Control Protocol

LISTA DE FIGURAS
Figura 2.1: Taxonomia para CV proposta em (CHOI et al., 2007). . . . . . . . . 21
Figura 3.1: Organização das camadas do simulador SimGrid. . . . . . . . . . . . 31
Figura 3.2: Ilustrando a interação entre as camadas do SimGrid e as principais
estruturas de dados. . . . . . . . . . . . . . . . . . . . . . . . . . . . 33
Figura 3.3: Estruturas de dados e camadas do SimGrid no simples caso de CV. . . 37
Figura 3.4: Tempo de execução vs. número de máquinas simuladas usando as
diferentes melhorias propostas (usando uma escala logarítmica em
ambos os eixos). . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41
Figura 3.5: Tempo de execução vs. número de máquinas simuladas usando as
diferentes melhorias propostas (usando uma escala logarítmica em
ambos os eixos). . . . . . . . . . . . . . . . . . . . . . . . . . . . . 42
Figura 3.6: Comparação do tempo de execução entre o BOINC Client Simulator
e o SimGrid. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 43
Figura 4.1: Utilidade para 2 projetos. Qualquer ponto na área cinza corresponde a
um possível resultado (outcome) da interação dos projetos. Diferentes
configurações dos projetos (ou estratégias) podem levar ao mesmo
resultado. A borda de Pareto (i.e., o conjunto de pontos que não são
dominados por nenhuma outra estratégia) é destacado com a linha em
negrito. Como o ilustrado, o equilíbrio de Nash pode ser dominado
por muitas outras soluções. . . . . . . . . . . . . . . . . . . . . . . . 53
Figura 5.1: Análise da influência do prazo de término e do intervalo de conexão
no CE e na perda usando a estratégia fixa de escalonamento. . . . . . 57
no CE e na perda usando a estratégia fixa de escalonamento. . . . . . 57
no CE e na perda usando a estratégia saturação de escalonamento. . . 58
no CE e na perda usando a estratégia saturação de escalonamento. . . 58
no CE e na perda usando a estratégia EDF de escalonamento. . . . . 60
no CE e na perda usando a estratégia EDF de escalonamento. . . . . 60
Figura 5.7: Influência da replicação no CE e perda usando uma estratégia fixa de
escalonamento para o projeto em rajadas. . . . . . . . . . . . . . . . 61
Figura 5.8: Comparando o CE e a perda das estratégias de escalonamento. . . . . 61

Figura 5.9: Análise da influência do tamanho dos lotes do projeto em rajada no
CE usando a estratégia de saturação no escalonamento. . . . . . . . . 62
Figura 5.10: Análise da influência do tamanho dos lotes do projeto em rajada na
perda usando a estratégia de saturação no escalonamento (note a es-
cala logarítmica no eixo Y). . . . . . . . . . . . . . . . . . . . . . . 63
Figura 5.11: Analisando o impacto dos projetos em rajadas no CE usando a estra-
tégia de escalonamento de saturação. . . . . . . . . . . . . . . . . . 63
Figura 5.12: Analisando o impacto dos projetos em rajadas na perda usando a es-
tratégia de escalonamento de saturação. . . . . . . . . . . . . . . . . 64
Figura 5.13: Analisando o impacto dos projetos em rajadas na perda usando a es-
tratégia de escalonamento fixa. . . . . . . . . . . . . . . . . . . . . . 64
Figura 5.14: Ilustrando o incentivo de um projeto alterar seu deadline a partir de
um estado de consenso. A linha de consenso representa o CE CEcons
de cada projeto em rajada se eles concordam com um certo deadline
σcons. A linha divergente representa quando um projeto dissidente
pode melhorar seu CEdis selecionando um deadline diferente σdis. O
impacto de tal modificação da estratégia no CE dos demais projetos
é representada pela linha CEnao−dis. . . . . . . . . . . . . . . . . . . 65
Figura 5.15: Esta figura retrata para um determinado σcons, a tendência de resposta
de σdis dos projetos em rajadas. Com tal informação, é possível ver o
resultado da estratégia de melhor resposta. . . . . . . . . . . . . . . . 66
Figura 5.16: Amostrando o conjunto de utilidade e ilustrando a ineficiência do
equilíbrio de Nash. 2 projetos contínuos e 4 projetos em rajadas com
900 tarefas de 1 hora por dia. CE pode ser melhorado em mais de
10% para todos os projetos caso seja escolhido, colaborativamente,
σcons = 1.15 ao invés do NE (σNE = 2.45). . . . . . . . . . . . . . . 67
Figura 5.17: Ilustrando o incentivo de um projeto alterar seu deadline a partir de
um estado de consenso. A linha de consenso representa o CE CEcons
de cada projeto em rajada se eles concordam com um certo deadline
σcons. A linha divergente representa quando um projeto dissidente
pode melhorar seu CEdis selecionando um deadline diferente σdis. O
impacto de tal modificação da estratégia no CE dos demais projetos
é representada pela linha CEnao−dis. . . . . . . . . . . . . . . . . . . 67
Figura 5.18: Esta figura retrata para um determinado σcons, a tendência de resposta
de σdis dos projetos em rajadas. Com tal informação, é possível ver o
resultado da estratégia de melhor resposta. . . . . . . . . . . . . . . . 68
Figura 5.19: Amostrando o conjunto de utilidade e ilustrando a ineficiência do
equilíbrio de Nash. 1 projeto contínuo e 7 projetos em rajadas com
600 tarefas de 1 hora por dia. CE pode ser melhorado mais de 10%
para os projetos em rajadas e de 7% para os projetos contínuos esco-
lhendo, colaborativamente, σcons = 1.25 ao invés do NE (σNE = 2.45). 68

LISTA DE TABELAS
Tabela 2.1: Principais características dos simuladores . . . . . . . . . . . . . . . 28
Tabela 3.1: Características dos projetos BOINC . . . . . . . . . . . . . . . . . . 43
Tabela 3.2: Número de tarefas completadas para o SimGrid e o BOINC Client
Simulator. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 46

RESUMO
Os avanços nas tecnologias de rede e nos componentes computacionais possibilitaram
a criação dos sistemas de Computação Voluntária (CV) que permitem que voluntários
doem seus ciclos de CPU ociosos da máquina para um determinado projeto. O BOINC é
a infra-estrutura mais popular atualmente, composta de mais 5.900.000 máquinas que pro-
cessam mais de 4.003 TeraFLOP por dia. Os projetos do BOINC normalmente possuem
centenas de milhares de tarefas independentes e estão interessados no throughput. Cada
projeto tem seu próprio servidor que é responsável por distribuir unidades de trabalho
para os clientes, recuperando os resultados e validando-os. Os algoritmos de escalona-
mento do BOINC são complexos e têm sido usados por muitos anos. Sua eficiência e
justiça foram comprovadas no contexto dos projetos orientados ao throughput. Ainda,
recentemente, surgiram projetos em rajadas, com menos tarefas e interessados no tempo
de resposta. Diversos trabalhos propuseram novos algoritmos de escalonamento para oti-
mizar seu tempo de resposta individual. Entretanto, seu uso pode ser problemático na
presença de outros projetos.
Neste texto, são estudadas as consequências do comportamento não cooperativo nos
ambientes de Computação Voluntária. Para realizar o estudo, foi necessário modificar o
simulador SimGrid para melhorar seu desempenho na simulação dos sistemas de CV. A
primeira contribuição do trabalho é um conjunto de melhorias no núcleo de simulação do
SimGrid para remover os gargalos de desempenho. O resultado é um simulador consi-
deravelmente mais rápido que as versões anteriores e capaz de rodar experimentos nessa
área.
Ainda, como segunda grande contribuição, apresentou-se como os algoritmos de es-
calonamento atuais do BOINC são incapazes de garantir a justiça e isolação entre os
projetos. Os projetos em rajadas podem impactar drasticamente o desempenho de todos
os outros projetos (rajadas ou não). Para estudar tais interações, realizou-se um detalhado,
multi jogador e multi objetivo, estudo baseado em teoria dos jogos. Os experimentos e
análise realizados proporcionaram um bom entendimento do impacto dos diferentes pa-
râmetros de escalonamento e mostraram que a otimização não cooperativa pode resultar
em ineficiências e num compartilhamento injusto dos recursos.
Palavras-chave: Computação voluntária, teoria dos jogos, escalonamento, simulação,
BOINC, simgrid.

ABSTRACT
Analyses of Non-Cooperative Behavior in Volunteer Computing Environments
Advances in inter-networking technology and computing components have enabled
Volunteer Computing (VC) systems that allows volunteers to donate their computers’ idle
CPU cycles to a given project. BOINC is the most popular VC infrastructure today with
over 5.900.000 hosts that deliver over 4.003 TeraFLOP per day. BOINC projects usually
have hundreds of thousands of independent tasks and are interested in overall throughput.
Each project has its own server which is responsible for distributing work units to clients,
recovering results and validating them. The BOINC scheduling algorithms are complex
and have been used for many years now. Their efficiency and fairness have been assessed
in the context of throughput oriented projects. Yet, recently, burst projects, with fewer
tasks and interested in response time, have emerged. Many works have proposed new
scheduling algorithms to optimize individual response time but their use may be prob-
lematic in presence of other projects.
In this text, we study the consequences of non-cooperative behavior in volunteer com-
puting environment. In order to perform our study, we needed to modify the SimGrid
simulator to improve its performance simulating VC systems. So, the first contribution
is a set of improvements in SimGrid’s core simulation to remove its performance bottle-
necks. The result is a simulator considerably faster than the previous versions and able to
run VC experiments.
Also, in the second contribution, we show that the commonly used BOINC schedul-
ing algorithms are unable to enforce fairness and project isolation. Burst projects may
dramatically impact the performance of all other projects (burst or non-burst). To study
such interactions, we perform a detailed, multi-player and multi-objective game theoretic
study. Our analysis and experiments provide a good understanding on the impact of the
different scheduling parameters and show that the non-cooperative optimization may re-
sult in inefficient and unfair share of the resources.
Keywords: Volunteer Computing, Game Theory, Scheduling, Simulation, BOINC, Sim-
Grid.

15
1 INTRODUÇÃO
A evolução da ciência nas últimas décadas, apoiada em infra-estruturas computacio-
nais, levou ao tratamento de problemas cada vez mais complexos. São muitos os casos
de pesquisas que requerem uma grande quantidade de processamento e a manipulação
de grande quantidade de dados. Um exemplo de aplicação é a modelagem climática do
planeta, na qual uma determinada simulação pode levar aproximadamente 3 meses numa
máquina com processamento de 1.4GHz (STAINFORTH et al., 2002). Considerando a
grande quantidade de simulações necessárias para exploração do modelo, até 2 milhões
com uma pequena variação dos parâmetros de entrada utilizados (STAINFORTH et al.,
2002), fica evidente a inviabilidade da execução dessas simulações numa única máquina.
A recente evolução nas tecnologias de conexão de rede e a diminuição na relação
custo/benefício dos componentes computacionais permitiram a criação de plataformas de
computação distribuída. Surgiram, então, ambientes como: clusters, os quais agrupam
componentes de prateleira interligados por redes dedicadas; e grades, nas quais computa-
dores de diversos domínios administrativos se unem para trabalhar para um mesmo fim.
Em sistemas distribuídos, os ambientes de Computação Voluntária (CV) possuem
também um importante destaque. Seu objetivo é agregar centenas de milhares de recursos
doados por pessoas comuns para trabalhar numa determinada aplicação. Esses recursos
normalmente são formados por máquinas de usuários comuns, muitas vezes afastados
geograficamente uns dos outros e conectados à rede através de um servidor de Internet.
Diversas plataformas foram criadas, tanto de cunho comercial quanto livre, tais como:
XtremWeb (CAPPELLO et al., 2004), BOINC (ANDERSON, 2004), Entropia (CHIEN
et al., 2003), Condor (THAIN; TANNENBAUM; LIVNY, 2002), entre outras. Entretanto,
foi o BOINC (Berkley Open Infrastructure for Networking Computing) que se tornou a
infra-estrutura de CV mais famosa e utilizada.
O BOINC possui, atualmente, mais de 5.900.000 máquinas, espalhadas por 272 países
e as quais são capazes de processar em média 4.003 TeraFLOPs por segundo (dados reti-
rados do site http://boincstats.com, em dezembro de 2010). Além disso, possui
diversos projetos científicos implantados, cujas áreas do conhecimento são as mais diver-
sas, tais como física de altas energias, biologia molecular, medicina, astrofísica, estudo
climáticos, entre outros. Abaixo, são apresentados alguns deles:
• SETI@home: projeto que visa a descoberta de sinais de vida alienígena através da
análise de ondas de rádio. É um dos mais antigos e populares projetos existentes;
• ClimatePrediction: através de modelos matemáticos complexos, propõe-se a prever
o comportamento climático da Terra até 2100;
• World Community Grid (WCG): na verdade, é um conjunto de projetos com fins

16
humanitários, tais como a cura de doenças, descoberta de novos remédios, novas
energias limpas, etc.
Os projetos do BOINC, normalmente, possuem milhares de tarefas CPU-bound e in-
dependentes, ou seja, tarefas cujo maior custo é o tempo de processamento e não a trans-
missão dos dados. Além disso, o número total de tarefas é muito maior que o número de
máquinas existentes na plataforma e por consequência, os projetos estão interessados no
número total de tarefas realizadas (throughput). Com esse objetivo, o BOINC implementa
diversas políticas de escalonamento que garantem o justo compartilhamento dos recursos
dos clientes, respeitando as prioridades individuais de cada projeto.
Diversos estudos, como (ANDERSON; MCLEOD VII, 2007) e (KONDO; ANDER-
SON; MCLEOD, 2007), provaram a eficiência e equidade das políticas de escalonamento
no contexto de projetos contínuos. Estes se caracterizam por possuírem uma grande quan-
tidade de tarefas independentes e estarem interessados no número total de tarefas com-
pletadas. Entretanto, a popularização das plataformas de CV indaga a sua utilização com
novos tipos de projetos, os quais não necessariamente possuam os mesmos tipos de ta-
refas dos já existentes. Nesse sentido, houve o surgimento de projetos em rajadas, ou
bursts. Em tais projetos, a carga de trabalho é composta de lotes com um número menor
de tarefas (Bag of Tasks) (SILBERSTEIN et al., 2009), os quais chegam em rajadas ao
sistema (e.g., 100 tarefas a cada dia) e contrastam com os projetos que possuem tarefas
continuamente. Por possuírem cargas de trabalho diferentes dos originais, esses projetos
podem necessitar de novas políticas de escalonamento no servidor para obter um bom
desempenho. Com essa finalidade, os trabalhos de (HEIEN; ANDERSON; HAGIHARA,
2009) e (KONDO; CHIEN; CASANOVA, 2007) propõem configurações diferentes para
otimizar o desempenho dos projetos em rajadas.
Contudo, como nos sistemas BOINC cada projeto possui seu próprio servidor, a in-
teração entre projetos com objetivos divergentes pode causar comportamentos não de-
sejáveis caso os projetos não tomem medidas preventivas sobre o assunto. Assim, foi
desenvolvido um estudo baseado em teoria dos jogos, cujo objetivo é verificar como o
comportamento não cooperativo dos projetos pode levar a resultados ineficientes e injus-
tiças no compartilhamento dos recursos dos clientes.
Geralmente, os estudos podem ser realizados através de 3 abordagens diferentes, são
elas:
Modelagem matemática: Nesse tipo de estudo é feita a descrição do comportamento da
aplicação através de equações matemáticas, para assim, analisar o seu desempe-
nho. Entretanto, devido à complexidade dos sistemas de computação voluntária, a
descrição e análise matemática se tornam extremamente difíceis.
Experimentação em ambientes reais: A utilização de plataformas reais para rodar pos-
síveis testes permite resultados fiéis ao verdadeiro comportamento do ambiente.
Porém, o uso de plataformas em produção pode gerar o desperdício de recursos e a
insatisfação dos usuários. Ainda, a construção de plataformas reais apenas para tes-
tes é custosa e extremamente difícil com um número de unidades de processamento
alto.
Experimentação em ambientes simulados: Outra alternativa é a utilização de uma pla-
taforma simulada, dentro de um ambiente controlado, permitindo a fácil explora-
ção das possibilidades de configurações. Como desvantagem de tal abordagem,

17
podemos citar a necessidade de utilização de simuladores conhecidos, nos quais os
resultados obtidos possam ser confiáveis.
Para realizar o estudo desejado, foi necessária a implementação de um simulador para
a arquitetura BOINC, além de, por questões de viabilidade e desempenho, realizar mo-
dificações no núcleo do simulador SimGrid utilizado. Estas permitiram melhorar o de-
sempenho do mesmo e realizar os experimentos necessários em tempo hábil. Maiores
detalhes sobre o simulador e as melhorias realizadas são apresentados durante o texto.
Em síntese, as principais contribuições deste trabalho são:
• Realizar a modelagem teórica baseada em teoria dos jogos do ambiente e realizar
experimentos a fim de verificar os potenciais problemas provenientes da interação
dos diferentes jogadores;
• Estudar a influência dos principais parâmetros de configuração no servidor no con-
texto de um ambiente com múltiplos jogadores;
• Mostrar o ocasional compartilhamento ineficaz e injusto dos recursos devido à in-
teração não cooperativa da configuração dos projetos interessados no tempo de res-
posta que compartilham recursos com projetos interessados no throughput;
• Implementar um simulador para a arquitetura BOINC que possua suas principais
funcionalidades e seja capaz de realizar tal estudo;
• Propor e implementar as modificações no SimGrid para este suportar a simulação
de ambientes de CV, avaliando o impacto dessas mudanças e comparando o novo
desempenho do simulador com algumas das alternativas existentes.
O restante do trabalho é dividido da seguinte maneira:
• O Capítulo 2 apresenta os trabalhos relacionados e os fundamentos necessários para
o desenvolvimento desta dissertação. Esse capítulo inclui a base em Computação
Voluntária (especialmente no BOINC) e simulação necessária;
• No Capítulo 3 é mostrado o simulador do BOINC proposto, detalhando os seus
principais componentes e funcionalidades. Além disso, são apresentados o funci-
onamento interno do simulador SimGrid e quais foram as modificações realizadas
para melhorar seu desempenho;
• Em seguida, o Capítulo 4 apresenta as notações teóricas usadas para modelar o
ambiente BOINC, utilizando para isso, os conceitos existentes na teoria dos jogos;
• O Capítulo 5 descreve os experimentos realizados e analisa os resultados obtidos,
discorrendo sobre a interação dos diferentes tipos de projetos no BOINC;
• Por fim, o Capítulo 6 exibe as conclusões finais do estudo e as possibilidades de
trabalhos futuros que poderão ser realizados.

19
2 TRABALHOS RELACIONADOS
O estudo de determinados problemas científicos necessitam da resolução de proble-
mas computacionais complexos de maneira eficiente. Muitas vezes esses problemas extra-
polam um tempo de execução razoável quando executado numa única máquina comum.
Neste contexto, o uso de supercomputadores torna-se uma alternativa, apesar de cara,
para diminuir o tempo de execução de tais problemas. Outra alternativa é a reunião de
recursos baratos de prateleira, formando plataformas de cálculo poderosas com um custo
baixo quando comparado aos supercomputadores. Um exemplo de tais plataformas é a
arquitetura Beowulf (STERLING et al., 1995) que é caracterizada por possuir recursos
homogêneos, confiáveis, fortemente acoplados, interligados por redes de conexão especí-
ficas e com gerenciamento de trabalhos centralizado.
Uma abordagem diferente surgiu em meados de 1990, com o desenvolvimento da
Computação em Grade, ou em inglês, Grid Computing. Segundo (FOSTER; KESSEL-
MAN; TUECKE, 2001), as grades são definidas pelo compartilhamento flexível e seguro
de recursos coordenados entre conjuntos de instituições independentes. Seus recursos são
normalmente heterogêneos, fracamente acoplados, dinâmicos e cujas tarefas são gerenci-
adas e escalonadas de forma distribuída.
Os sistemas baseados em roubo de ciclos (cycle stealing) que utilizam ciclos ociosos
das máquinas têm seu começo no projeto PARC Worm (SHOCH; HUPP, 1982), o qual
replicava a sua aplicação nos recursos livres que encontrava no sistema. As plataformas
fundadas na doação e agregação de recursos livres foram sendo criadas e evoluídas, sendo
conhecidas como plataformas de Computação Voluntária.
2.1 Computação Voluntária
A Computação Voluntária (CV), em inglês Volunteer Computing (VC), é um tipo de
sistema distribuído cujo objetivo é colher recursos ociosos de máquinas para o melhor
aproveitamento das mesmas. Quando esses recursos pertencem a uma mesma instituição,
normalmente dentro de uma rede local, a estrutura é chamada Desktop Grid. A Compu-
tação Voluntária, por outro lado, agrega recursos que são doados por usuários comuns,
normalmente interligados através da rede global de computadores. Os recursos doados
podem ser os mais variados, desde processamento de CPU, GPU, disco, entre outros. CV
tornou-se famosa graças ao projeto SETI@home (ANDERSON et al., 2002), o qual teve
seu início em 1999 e visa a procura de vida extraterrestre. Antes dele, dois outros pro-
jetos foram criados, o GIMPS e Distributed.net, porém sem alcançar o mesmo sucesso.
Mais tarde, o código fonte do SETI@home foi refatorado e aberto, transformando-se na
plataforma hoje conhecida como BOINC.
O trabalho de (CHOI et al., 2007) propõe uma taxonomia para a área, apresentada na

20
Figura 2.1 e detalhada abaixo:
Organização: Indica como é feito o gerenciamento dos recursos e se divide em 2 cate-
gorias:
• Centralizada: Possui um servidor central que gerencia a plataforma e é res-
ponsável por distribuir as tarefas aos provedores de recurso;
• Distribuída: Por outro lado, a organização distribuída não possui servidor cen-
tral e a responsabilidade é dividida entre os voluntários.
Plataforma: Classifica o ambiente conforme os aplicativos necessários pelo provedor do
recurso para participar do ambiente.
• Web-based: Esse tipo de plataforma é baseada em tecnologias web e são dis-
ponibilizadas através de applets pela Internet. Ao usuário basta acessar o site
e o aplicativo é baixado e roda na sua máquina;
• Middleware: Necessita a instalação de um programa específico na máquina
do usuário que é responsável por gerenciar os recursos existentes.
Escala: Representa a abrangência do sistema. São elas:
• Internet: Qualquer máquina conectada à Internet pode participar;
• LAN: Normalmente restrito a um ambiente fechado, tais como empresas ou
universidades.
Provedor de Recurso: Caracteriza de onde vem os recursos do ambiente:
• Voluntário: São os usuários totalmente voluntários, os quais não possuem
qualquer ligação com os projetos para os quais estão trabalhando;
• Empresa: Composto por máquinas que pertencem a uma organização e por
isso, devem participar da plataforma.
Segundo (KONDO et al., 2004), os ambientes de computação voluntária têm as se-
guintes características:
• Volatilidade: Uma consequência direta do caráter voluntário da doação dos recursos
é a volatilidade dos mesmos. Cada cliente pode entrar, sair ou retirar elementos do
sistema a qualquer momento, independente do recurso estar sendo usado ou não;
• Heterogeneidade: Cada máquina da plataforma possui suas características (sistema
operacional, processador, disco, RAM, etc). Dessa forma, a aplicação que roda em
uma determinada máquina pode não rodar em outra;
• Escalabilidade: O sistema é facilmente escalável uma vez que a simples adesão de
novos clientes aumenta a capacidade de processamento da plataforma;
• Imprevisibilidade: Devido, principalmente, ao dinamismo dos clientes, é extrema-
mente difícil prever o comportamento do sistema.

21
Provedor de Recurso
Computação Voluntária
Descentralizada
Middleware
LAN
Centralizada
Organização
Plataforma
Escala
Internet
Empresa
Voluntário
Web−based
Figura 2.1: Taxonomia para CV proposta em (CHOI et al., 2007).
A carga de trabalho da maioria dos projetos que utilizam os recursos de CV é com-
posta de uma grande quantidade de tarefas independentes, em número muito maior que a
quantidade de máquinas disponíveis. Essas tarefas são limitadas pela quantidade de pro-
cessamento necessária para sua finalização. Os projetos, por sua vez, usualmente estão
interessados em obter a maior quantidade possível de tarefas num determinado período
de tempo, ou seja, sua métrica é o throughput. Diversos trabalhos tratam de técnicas para
melhorar o desempenho do sistema com tais características.
No trabalho de (ESTRADA; TAUFER; ANDERSON, 2009) são estudados: as po-
líticas na seleção de tarefas a serem enviadas aos clientes, isto é qual o tipo e em que
quantidade as tarefas devem ser selecionadas; o desempenho no uso de redundância ho-
mogênea na distribuição das tarefas, evitando a perda de resultados devido à variabilidade
numérica decorrente de diferenças nas configurações das máquinas utilizadas; e a relação
entre a taxa de erros das tarefas e o nível de replicação utilizado, constatando a melhor
quantidade de réplicas a serem usadas em cada caso. Já em (ESTRADA et al., 2006), os
autores propõem o uso de políticas de escalonamento baseada em limiares na disponibili-
dade e confiabilidade dos clientes na hora do envio das tarefas.
A evolução destas plataformas e a sua popularização desafiam o seu uso com novas
classes de carga de trabalho, cujas características sejam diferentes das atuais. Uma classe
promissora são os lotes de tarefas (batch) com um número relativamente pequeno de ta-
refas, em intervalos não constantes de tempo. Como esses projetos não possuem tarefas
regularmente, eles não estão interessados no número total de tarefas, mas sim, no tempo
médio de respostas dos lotes. Neste contexto, alguns trabalhos apresentam novos algorit-
mos que visam melhorar seu desempenho.
O trabalho de (KONDO; CHIEN; CASANOVA, 2007) afirma que um rápido tempo
de resposta das aplicações pode ser obtido através de:
• Priorização dos recursos: O ordenamento dos recursos conforme algum critério, tal
como o poder de processamento da CPU ou média de tarefas realizadas, pode evitar
a distribuição de tarefas para as máquinas consideradas ruins. Nota-se que essa

22
abordagem para diminuir o tempo de resposta funciona caso o número de tarefas
seja menor que o número de máquinas disponíveis;
• Exclusão de recursos: Consiste na remoção dos recursos, seja por um critério fixo
(limiar no poder de processamento), seja pela predição do tempo que o host demo-
rará para concluir uma tarefa;
• Replicação de tarefas: A falha de uma tarefa ou um host lento executando uma ta-
refa no fim do lote, ocasiona um retardo no término do mesmo. Para evitar esse
fenômeno, pode-se enviar essa mesma tarefa para ser executada em mais de 1 má-
quina, e dessa forma, obter a resposta mais rapidamente.
Uma configuração importante nos sistemas de CV é o intervalo de conexão dos clien-
tes com o servidor, pois ele determina a reatividade que os clientes terão às novas tarefas.
Na pesquisa descrita em (HEIEN; ANDERSON; HAGIHARA, 2009) é investigada qual
a frequência que os clientes devem se conectar para que um determinado número de co-
nexões ocorra num intervalo de tempo, garantindo assim, um número mínimo de clientes
para trabalhar num certo lote.
Por fim, o projeto GridBot (SILBERSTEIN et al., 2009) utiliza um ambiente híbrido,
composto de clusters, grids e CV para a execução de cargas de trabalho mistas, contendo
projetos interessados no throughput e no tempo de resposta. A plataforma leva em consi-
deração o estado do lote sendo executado para escalonar as tarefas (e.g., últimas tarefas do
lote são escalonadas nos recursos mais confiáveis para não atrasar a entrega do mesmo).
2.2 BOINC
O BOINC (Berkley Open Infrastructure for Networking Computing) (ANDERSON,
2004) é uma das infra-estruturas mais conhecidas e utilizadas atualmente em Computa-
ção Voluntária. O BOINC utiliza uma arquitetura clássica do tipo cliente/servidor, onde
cada projeto tem um servidor específico do qual os clientes obtêm tarefas a serem execu-
tadas. Durante o processo de instalação do cliente BOINC, o usuário define para quais
projetos ele deseja trabalhar, além de especificar a prioridade entre eles. Em seguida, são
apresentados os detalhes de funcionamento do cliente e do servidor.
2.2.1 Cliente
O usuário, ao decidir participar da plataforma BOINC, deve instalar um aplicativo e
escolher para quais projetos deseja colaborar. Esse programa possui políticas de escalo-
namento próprias responsáveis por gerenciar as tarefas executadas na máquina. O usuário
tem preferências que podem ser configuradas, incluindo:
• Compartilhamento dos recursos para cada projeto: A fração de cada recurso que é
disponibilizada para cada projeto;
• Limites no uso do processador: Estabelecer uma porcentagem do processador que
pode ser usada, evitando por exemplo, um aquecimento excessivo do mesmo;
• Máxima quota de memória RAM disponível: O usuário pode limitar o uso da RAM
pelos aplicativos do BOINC;
• ConnectionInterval: Estabelece o período típico entre conexões do cliente aos ser-
vidores do BOINC;

23
• SchedulingInterval: Define a fatia de tempo padrão do uso do processador pelos
aplicativos (o valor padrão é de 1 hora).
De acordo com (ANDERSON; MCLEOD VII, 2007), a política de escalonamento do
cliente possui os seguinte objetivos:
• Maximizar a quantidade de crédito dada ao usuário, para isso, deve manter a CPU
o máximo de tempo ocupada e evitar a perda dos prazos das tarefas;
• Reforçar o compartilhamento justo dos recursos entre os projetos no longo prazo;
• Maximizar a variedade das tarefas executadas pelo cliente, ou seja, evitar longos
períodos executando tarefas de um único projeto.
2.2.1.1 Escalonamento
O escalonamento do cliente é dividido, basicamente, em 2 conceitos. O primeiro, trata
de decidir qual a tarefa entre as disponíveis irá executar na CPU num dado momento. O
segundo, verifica a necessidade de solicitar novas tarefas aos projetos, ou seja, determina,
baseado nas configurações e na carga de trabalho atual, a quais projetos e quantas tarefas o
cliente deve solicitar. Antes de apresentar as políticas de escalonamento, alguns conceitos
devem ser explicados:
• Debt(P): é a quantidade de processamento devida pelo cliente ao projeto P; ela é
calculada segundo a prioridade do projeto e as suas tarefas executadas;
• DeadlineMissed: são as tarefas que estão próximas de perder seu prazo de término;
• Shortfall(P): é a quantidade de trabalho adicional necessária para manter o cliente
ocupado com o projeto P durante um determinado período.
Escalonamento na CPU: Em linhas gerais, o escalonamento das tarefas pode ser di-
vidido em 2 grupos principais. Primeiramente, são escalonadas as tarefas contidas
em DeadlineMissed, por ordem crescente de prazo de término, ou seja, primeiro
aquelas que estão mais perto de perder seu prazo. Após isso, é selecionado o pro-
jeto P cujo Debt(P) seja maior, isto é, para qual o cliente tenha trabalhado menos. O
escalonamento continua dessa maneira até que todos os recursos sejam utilizados.
Política de requisições de tarefas: Por padrão, o cliente seleciona o projeto P para o
qual ele menos trabalhou no longo prazo. Para este, é solicitado uma quantidade
de trabalho igual ao seu Shortfall(P), mantendo-o assim, ocupado até a próxima
conexão ao servidor. Uma exceção a esse padrão ocorre quando o projeto está
overworked, ou seja, quando o cliente trabalhou muito tempo para um mesmo pro-
jeto. Nesse caso, o cliente desconsidera o projeto na hora de solicitar novas tarefas.
Esse fenômeno pode ocorrer, por exemplo, quando o projeto possui tarefas com
prazos de término extremamente curtos, fazendo com que estas passem na frente
das outras.
Logo, os clientes tentam compartilhar de maneira justa (instantaneamente) os recur-
sos entre os projetos, respeitando suas prioridades. Entretanto, o compartilhamento justo
instantâneo pode causar overhead que reduz o throughput do cliente e atrasa o término
das tarefas. Portanto, o cliente BOINC implementa um algoritmo de escalonamento que

24
mescla a equidade dos projetos no curto e longo prazo. A exceção é quando uma tarefa
está próxima de perder seu prazo de finalização. Neste instante, o algoritmo muda para
o modo EDF e executa essas tarefas com uma prioridade maior, evitando assim que a
tarefa não seja completada no prazo e o cliente perca os créditos referentes a ela. Conse-
quentemente, projetos contínuos geralmente possuem deadline longo, enquanto projetos
em rajadas tendem a ter prazos curtos, já que estas são executadas com maior prioridade.
É importante, contudo, ressaltar que o mecanismo de compartilhamento a longo prazo
evita que projetos com tarefas de deadline curto sempre ultrapassem as outras. Quando
um cliente trabalhou demais para um mesmo projeto, ele simplesmente não solicita novas
tarefas desse projeto.
2.2.2 Servidor
A principal atividade do servidor é distribuir tarefas aos clientes. Ao receber uma
requisição de um cliente, ele seleciona aquela que melhor se adapta de uma lista de tare-
fas disponíveis. Ainda, o servidor deve considerar as restrições do sistema (processador,
RAM, etc) que podem evitar que o cliente rode as tarefas corretamente. Devido à volati-
lidade dos usuários, o servidor é responsável também por armazenar o estado das tarefas
que foram distribuídas aos clientes, isto é, verificar, através de um mecanismo de prazo
de término, quando é preciso reenviar alguma tarefa. Ao enviar uma tarefa o servidor
determina um prazo máximo no qual ela deve retornar. No caso da tarefa ser entregue
no prazo, um bônus em pontos é oferecido ao cliente, caso contrário, nenhum crédito é
ofertado a ele.
Neste trabalho, são analisados 2 tipos de projetos:
Projetos contínuos: Tais projetos possuem uma quantidade de tarefas independentes ex-
tremamente grande. Portanto, estão interessados no throughput geral de tarefas,
isto é, no número de tarefas completadas por dia. A maior parte dos projetos atuais
do BOINC estão inseridos nesta categoria.
Projetos em rajadas: Ao contrário dos projetos da categoria anterior, estes recebem lo-
tes de tarefas (Bag of Tasks) e estão interessados no tempo de resposta médio dos
lotes.
De modo a obter melhores desempenhos, o servidor pode usar algumas estratégias,
tais como replicação, deadline, intervalo de conexão ou políticas de escalonamento. Elas
são descritas rapidamente a seguir:
Replicação: Um dos usos da replicação visa melhorar o tempo médio de resposta, evi-
tando assim, o problema de término da última tarefa do lote (KONDO; CHIEN;
CASANOVA, 2007). Este problema ocorre quando as últimas tarefas do lote estão
sendo executadas e devido a uma máquina mais lenta, algumas tarefas são atra-
sadas, e consequentemente, retardam todo o processamento do lote. A replicação
possui algumas variações, apresentadas em (ANDERSON; REED, 2009):
• Redundância Homogênea: Neste caso, as tarefas são distribuídas somente aos
clientes que possuam máquinas com as mesmas características (OS, CPU). A
redundância homogênea é utilizada, principalmente, com aplicações instáveis,
nas quais pequenas variações decorrentes do sistema utilizado podem gerar
resultados completamente diferentes;

25
• Replicação Adaptativa: Na medida que grande parte dos usuários produzem
resultados corretos (KONDO et al., 2007), a replicação adaptativa replica as
tarefas para a conferência dos resultados somente se o cliente é considerado
não confiável. Dessa maneira, evita-se o desperdício maior dos recursos cau-
sado pela replicação.
Prazo de término (Deadline): O deadline é usado para manter o rastro da execução das
tarefas nos clientes. Os prazos mais curtos implicam maior interação entre o cli-
ente e o servidor. Ainda, o deadline também pode ser usado para dar prioridade a
determinadas tarefas.
Intervalo de conexão: Como todas as comunicações são iniciadas pelo cliente (devido
às restrições de conectividade dos clientes, tais como firewall ou NAT), o servidor
não pode contatar diretamente os usuários. O intervalo de conexão é, portanto,
utilizado para indicar quando o servidor deseja que o cliente se conecte novamente.
Nota-se que apesar da indicação, não há nenhuma garantia que o cliente irá se
reconectar realmente.
Política de escalonamento: O servidor pode utilizar alguma política especial na seleção
de tarefas que são distribuídas aos clientes. Em resumo, são apresentadas abaixo:
• Fixa (Fixed): O servidor não realiza nenhum tipo de teste antes de enviar a
tarefa ao cliente;
• Saturação (Saturation): O servidor recebe o tempo de saturação do cliente,
isto é, a data na qual o cliente irá terminar de executar todas as tarefas urgentes
que ele possui (rodando em modo EDF). Então, o servidor verifica se a tarefa
que ele deseja enviar, começando após a data de saturação, é capaz de terminar
dentro do prazo estipulado. Em caso positivo a tarefa é enviada, caso contrário
não;
• EDF (Earliest Deadline First): É o teste mais restritivo dos três, pois ele rea-
liza uma simulação detalhada de todas as tarefas rodando no cliente. O nome
vem do fato do servidor utilizar a política de escalonamento EDF para ve-
rificar o comportamento das tarefas no sistema. O servidor, no momento de
selecionar uma tarefa, adiciona-a na lista das tarefas existentes, realiza a simu-
lação EDF e verifica se nenhuma tarefa é atrasada devido à inserção da nova.
Se não houver atrasos, a tarefa é enviada.
A configuração padrão do BOINC utiliza o teste de saturação, entretanto os projetos
têm a liberdade de ativar ou desativar as políticas conforme as necessidades de sua carga
de trabalho, seus objetivos e as características dos clientes, a fim de possibilitar o melhor
comportamento possível (e.g., throughput ou tempo de resposta).
2.3 Simulação
Como citado anteriormente, para a realização do estudo proposto nesta dissertação é
imprescindível a utilização de um simulador a fim de executar os experimentos neces-
sários. Esta seção apresenta as principais opções disponíveis atualmente no contexto de
simulação de ambientes de Computação Voluntária, com ênfase nos simuladores da ar-
quitetura BOINC.

26
2.3.1 Simuladores específicos do BOINC
Diversos simuladores foram propostos para o estudo dos componentes da arquite-
tura BOINC, tais como BOINC Client Simulator, SimBA (TAUFER et al., 2007), Sim-
BOINC (KONDO, 2007) e EmBOINC (ESTRADA et al., 2009). Mais detalhes são apre-
sentados a seguir:
BOINC Client Simulator: O pacote em que o BOINC é distribuído possui um simula-
dor para o estudo de um simples cliente interagindo com diferentes projetos. O
simulador usa um modelo de host simplificado, no qual são especificados o número
de processadores, o poder de processamento e a quantidade de memória RAM. Os
períodos de disponibilidade e indisponibilidade são modelados através de funções
exponenciais. Por outro lado, tanto a rede de interconexão quanto o disco não são
modelados.
O BOINC Client Simulator foi utilizado em diversos estudos, tais como (ANDER-
SON; MCLEOD VII, 2007) e (KONDO; ANDERSON; MCLEOD, 2007). Por uti-
lizar o próprio código fonte do BOINC, podemos considerar seus resultados confiá-
veis. Por outro lado, a necessidade de codificação direta no código fonte do BOINC
torna o estudo de novos algoritmos mais difícil.
SimBA: Criado para o estudo de políticas de escalonamento do servidor, o SimBA simula
1 servidor interagindo com um conjunto de clientes. O simulador é baseado em uma
máquina de estados finitos, parametrizada com as características do sistema. Para
simular a natureza volátil de CV, ele utiliza uma distribuição gaussiana para modelar
o atraso na execução das tarefas. Além disso, utiliza uma distribuição uniforme para
determinar o estado final de uma tarefa (válida, inválida, etc).
O SimBA foi utilizado no trabalho de (ESTRADA et al., 2006) e por ser extrema-
mente simples, alcança bons níveis de escalabilidade. Entretanto, a simulação é
limitada a um único projeto.
EmBOINC: Assim como o SimBA, o EmBOINC foi proposto para o estudo de políticas
de escalonamento do servidor, tal como em (ESTRADA; TAUFER; ANDERSON,
2009). Porém, seu modo de funcionamento é diferente. Enquanto o SimBA simula
o comportamento do cliente e do servidor, o EmBOINC utiliza o código fonte mo-
dificado do próprio BOINC, no qual o servidor roda em modo emulado. Por outro
lado, os clientes são simulados e geram requisições reais de tarefas ao servidor.
Para simular a volatilidade dos clientes, distribuições gaussianas modelam o atraso
na execução de tarefas, uma distribuição weibull modela o intervalo de conexão ao
servidor e distribuições uniformes determinam o estado final de uma tarefa.
Novamente, esse simulador é interessante para o estudo das políticas de escalona-
mento atuais do servidor, entretanto não permite o estudo de vários projetos intera-
gindo ao mesmo tempo e toda a modificação do escalonamento deve ser implemen-
tada diretamente no código fonte do BOINC.
SimBOINC: Em (CAPPELLO et al., 2009) é utilizado um simulador chamado Sim-
BOINC. Baseado no código fonte modificado do BOINC, ele utiliza o simulador
SimGrid como base para os modelos de rede e CPU, dessa forma permite o estudo
de ambientes complexos, compostos de vários clientes e servidores (fato que não
ocorre nos demais). Um dos grandes problemas desta abordagem é a necessidade

27
de mantê-lo atualizado conforme a implementação do BOINC for modificada. A
última versão do SimBOINC é compatível com a versão 5.5.11 do BOINC, no en-
tanto, ele não é mais mantido e está defasado (versão de maio de 2011 é a 6.10.58).
2.3.2 Simuladores de propósito geral
Diversos simuladores foram desenvolvidos ao longo do tempo para o estudo na área de
computação distribuída, entretanto a maioria tem curta duração de vida (NAICKEN et al.,
2006). Pode-se citar dois que resistiram ao tempo, o GridSim (BUYYA; MURSHED,
2002) e o SimGrid (CASANOVA, 2001; CASANOVA; LEGRAND; QUINSON, 2008).
GridSim: O GridSim foi desenvolvido para fornecer uma ferramenta de simulação de
grades e clusters que tivesse capacidade de modelar os mais diferentes tipos de
entidades desses ambientes. Entre as funcionalidades, podemos citar:
• Modelagem de recursos heterogêneos;
• Definição da hierarquia de rede que interliga os nós;
• Disponibilidade dos recursos através de arquivos de traços;
• Geração de informações sobre a execução para posterior análise.
Apesar do GridSim ser genérico, permitindo assim, o estudo da área de Computa-
ção Voluntária, os trabalhos de (DEPOORTER et al., 2008) e (BARISITS; BOYD,
2009) mostram que ele possui sérios problemas de escalabilidade que levantam a
dúvida da sua capacidade de simular ambientes de CV.
SimGrid: O SimGrid também é um simulador de propósito geral, mantendo portanto,
as características comuns de tal tipo de plataforma. Foi utilizado recentemente no
estudo de CV (HEIEN; FUJIMOTO; HAGIHARA, 2008) e é capaz de simular até
200.000 hosts numa máquina com 4GB de memória RAM (The SimGrid project,
2011). Ele foi usado ainda, em estudos do projeto OurGrid (SANTOS-NETO et al.,
2004; MOWBRAY et al., 2006) e no escalonamento de tarefas do tipo Bag of Tasks
em (SILVA; SENGER, 2009).
Além disso, um dos atrativos do SimGrid é o o constante esforço realizado por seus
desenvolvedores de forma a tornar seus modelos mais próximos da realidade. Por
exemplo, o trabalho de (VELHO; LEGRAND, 2009) efetua um estudo para tornar
mais preciso os modelos de rede utilizados no simulador. Apesar dos animado-
res resultados do SimGrid, no recente estudo com algumas centenas de máquinas
executado em (HEIEN; FUJIMOTO; HAGIHARA, 2008), Heien et al. identificou
alguns cenários simples onde o simulador possui um tempo de execução inaceita-
velmente alto.
A Tabela 2.1 resume as principais características dos simuladores analisados anterior-
mente. São apresentados os números de clientes e servidores que podem ser simulados,
além das principais vantagens e desvantagens dos simuladores.

28
Simulador Número Cli-
entes
Número Ser-
vidores
Principais Vantagens Principais Desvanta-
gens
BOINC
Client Simu-
lator
1 N Fiel ao comporta-
mento cliente
Novos algoritmos di-
retamente no código
do BOINC, apenas 1
cliente
SimBA N 1 Escalável Modelo simplificado,
restrito 1 servidor
EmBOINC N 1 Fiel ao comporta-
mento do servidor
Novos algoritmos di-
retamente no código
do BOINC
SimBOINC N N Estudo de ambientes
complexos
Desatualizado
GridSim N N Genérico Problemas de escala-
bilidade
SimGrid N N Genérico Problemas de desem-
penho
Tabela 2.1: Principais características dos simuladores
2.4 Considerações Finais
Este capítulo apresentou os principais conceitos relacionados à área de Computa-
ção Voluntária, em especial a plataforma BOINC. Viu-se que o bom funcionamento do
BOINC foi provado no contexto de aplicações interessadas no número total de tarefas re-
alizadas. Além disso, foram mostradas diversas abordagens para o uso de tais plataformas
com aplicações interessadas no tempo de resposta. Contudo, não foi encontrado nenhum
estudo no sentido de analisar os resultados do comportamento dos projetos no compar-
tilhamento dos recursos. Este trabalho visa abordar tal problema, permitindo assim, a
melhor compreensão das plataformas de CV.
Posteriormente foram analisadas os principais ferramentas disponíveis para a pesquisa
de CV. Os simuladores foram divididos em 2 grandes categorias: de propósito geral e es-
pecíficos do BOINC. Como visto, os de propósito geral são genéricos e permitem a mo-
delagem do ambiente de CV desejado. Por outro lado, necessitam um esforço maior para
descrever toda a arquitetura do BOINC. Já os simuladores específicos possuem a vanta-
gem de ter a arquitetura do BOINC pronta, mas carregam restrições que podem diminuir
a quantidade de estudos realizáveis. A comparação realizada permitiu verificar os prós
e contras de cada simulador de forma a escolher o que melhor se adapta aos requisitos
do estudo. Conclui-se que os simuladores existentes não satisfazem completamente as
exigências necessárias (múltiplos clientes e servidores, escalabilidade, desempenho, faci-
lidade de uso, etc). Por isso, optou-se por realizar as modificações descritas no Capítulo 3.

29
3 SIMULADOR DO BOINC
Este capítulo apresenta o desenvolvimento do simulador da arquitetura BOINC que
será usado no restante do estudo. Além da descrição das características do simulador
proposto, são mostradas as modificações realizadas no núcleo de simulação do SimGrid,
as quais eram de vital importância para o bom andamento do trabalho.
3.1 Introdução
A grande maioria dos estudos em Computação Voluntária são feitos empiricamente,
através da execução de experimentos. Infelizmente, a utilização de plataformas reais
para o estudo é desafiador, uma vez que os sistemas de CV em produção raramente es-
tão disponíveis para testes. Além disso, seu uso pode interferir na carga de trabalho do
sistema, causar o descontentamento dos usuários e por consequência, seu desligamento
do sistema. Ainda, a implantação de um sistema de CV apenas para experimentos é ex-
tremamente cara e difícil, também a escala alcançada com tal abordagem é no máximo
moderada e não representativa de um sistema real. Por fim, a capacidade de reprodução
dos experimentos é muito importante e a volatilidade dos clientes torna essa tarefa impro-
vável num ambiente real. Por essas razões, os estudos desenvolvidos neste trabalho são
realizados utilizando ambientes simulados.
O próximo passo a ser feito é a escolha do simulador a ser utilizado. Este deve ser
capaz de rodar experimentos onde múltiplos servidores de projetos interagem com uma
certa quantidade de clientes. Além disso, as características de CV necessitam ser abran-
gidas, tais como a volatilidade dos clientes, escalabilidade e heterogeneidade. Pode-se
dividir os desafios da simulação em Computação Voluntária em 4 eixos principais:
Simulando os hosts: A abordagem mais flexível é a utilização de processos para a simu-
lação do comportamento de cada máquina do sistema, através da execução de um
código arbitrário. O principal problema de tal abordagem é a escalabilidade. Por
exemplo, a simulação de 1 milhão de hosts numa única máquina com 4GB de RAM
restringe a utilização de no máximo 4KB para descrever cada processo. Os simu-
ladores de propósito gerais, tais como SimGrid e GridSim, recaem nessa categoria.
Uma alternativa é a utilização de máquinas de estado finitas para representar as má-
quinas, alcançando assim, uma escalabilidade maior. Entretanto, essa abordagem
restringe a flexibilidade do simulador e o afasta da realidade. Alguns simuladores,
como o SimBA por exemplo, utilizam máquinas de estado para obter simulações
escaláveis.
Simulando a rede: Uma opção é desconsiderar a rede, assumindo que cada comunica-
ção leva um tempo fixo (possivelmente zero), ou ainda, um tempo proporcional ao

30
tamanho da tarefa. Isto é largamente utilizado nas pesquisas em CV, uma vez que
grande parte dos projetos são limitados pelo poder de processamento e não pos-
suem muitos dados a serem transmitidos. Entretanto, para outros tipos de estudos,
a simulação correta da rede pode ser importante. Nesta categoria, a grande parte
dos simuladores do BOINC (SimBA, EmBOINC, BOINC Client Simulator) optam
por não simular a rede, apenas o SimBOINC, o qual utiliza o SimGrid como base
de simulação, permite tal estudo.
Simulando volatilidade: Como dito anteriormente, a volatilidade é uma característica
importante em CV. A abordagem mais realística é a utilização de traços reais de
máquinas coletados de sistemas de CV em funcionamento (KONDO et al., 2010).
Porém, tal abordagem eleva uma dúvida quanto a sua escalabilidade, já que os
traços podem ser numerosos e grandes, e consequentemente, o tempo e memória
necessários para armazená-los e processá-los pode ser elevado. A alternativa para
atingir níveis de escalabilidade maiores é o uso de distribuições estatísticas para
modelar a disponibilidade das máquinas (KONDO et al., 2004, 2007). Embora
algumas distribuições candidatas tenham sido descobertas, tais como no estudo
de (NURMI; BREVIK; WOLSKI, 2005), não é totalmente claro o quão realistas
elas são. Os simuladores específicos do BOINC, em geral, utilizam distribuições
para modelar a volatilidade, enquanto os de propósito geral usam os arquivos de
traços das máquinas.
Escolhendo a precisão de tempo: A escolha da precisão do avanço do tempo é um im-
portante problema, uma vez que pesquisadores podem estar interessados tanto em
noções a longo prazo (tempo médio ativo da máquina) ou curto prazo (número de
vezes que uma tarefa foi suspensa). A abordagem mais precisa, porém menos es-
calável, é o uso de eventos discretos. Nesse tipo de simulação, o tempo avança
conforme os eventos vão acontecendo. Outra possibilidade é a simulação orientada
por intervalos de tempo, onde o tempo simulado avança em passos fixos, possivel-
mente grandes, e então são calculados os eventos que ocorreram nesse intervalo.
Com tal abordagem é possível modificar o passo escolhido de forma a conseguir
maior ou menor escalabilidade. Contudo, a escolha do parâmetro ideal entre preci-
são e escalabilidade pode ser problemática.
Analisando as vantagens e desvantagens das opções de simuladores disponíveis, optou-
se por utilizar o SimGrid. O SimGrid é um simulador baseado em eventos que provê um
framework de simulação capaz de fornecer resultados confiáveis. O SimGrid reúne algu-
mas das principais características desejáveis para CV, tais como o uso de código genérico
para os processos, a simulação da rede e o uso de arquivos de traços para as máqui-
nas. Avaliando os concorrentes, a necessidade de simulação de vários projetos e usuá-
rios do ambiente do BOINC restringe a utilização dos principais simuladores disponíveis
(BOINC Client Simulator, EmBOINC e SimBA). O SimBOINC permitiria tal estudo, en-
tretanto a versão do BOINC que ele suporta está desatualizada. Ainda, o GridSim foi
descartado devido aos problemas de desempenho e escalabilidade apontados nos traba-
lhos de (DEPOORTER et al., 2008) e (BARISITS; BOYD, 2009).
Apesar de todas as vantagens apontadas para a utilização do SimGrid, os problemas
de desempenho identificados por Heien durante o trabalho (HEIEN; FUJIMOTO; HA-
GIHARA, 2008) impossibilitariam o estudo desejado, uma vez que as simulações pode-
riam levar muito tempo para serem finalizadas. Diante disso, foram propostas e imple-

31
GRE:
GRAS
in
situ
SURF
SimIX
SMURF
SMPI GRAS
MSG
SimDag
XBT
"POSIX-like"API on a virtual platform
SimIX network proxy
virtual platform simulator
Figura 3.1: Organização das camadas do simulador SimGrid.
mentadas melhorias no simulador SimGrid, de forma a sanar esses problemas e tornar
possível a execução dos testes num tempo razoável.
O restante do capítulo é dividido da seguinte forma: a Seção 3.2 apresenta os detalhes
do simulador SimGrid, além de seu funcionamento interno, as modificações propostas
e a avaliação das mesmas. Por fim, a Seção 3.3 apresenta a implementação do ambi-
ente BOINC realizada utilizando o SimGrid, detalhando os principais componentes e as
decisões tomadas no design do mesmo. Por fim, uma breve validação do simulador é
apresentada.
3.2 SimGrid
O projeto SimGrid foi iniciado há aproximadamente uma década para o estudo de
aplicações distribuídas em ambientes de grade (CASANOVA, 2001). Em tais ambien-
tes, as plataformas são complexas (compostas por recursos heterogêneos, arquiteturas de
rede hierárquicas, disponibilidade dinâmica dos recursos, etc) e os algoritmos de escalo-
namento devem ser concebidos com base em versões tratáveis da plataforma. Assim, o
objetivo primordial do SimGrid era fornecer uma ferramenta para o estudo de algoritmos
de escalonamentos em ambientes complexos de grade.
A arquitetura do simulador, apresentada na Figura 3.1, possui 4 APIs (Application
Programming Interfaces) para os usuários, as quais são descritas abaixo:
• MSG: Fornece uma API simples para o estudo de aplicações distribuídas. Imple-
mentada em C, possui interfaces para Java, Lua e Ruby. MSG é a interface mais
simples de uso, permitindo de maneira fácil a implementação dos algoritmos a se-
rem testados;
• GRAS (Grid Reality And Simulation): O GRAS foi desenvolvido com o intuito de
unir a execução real de aplicativos com a execução em ambientes simulados. Desse
modo, é possível testar e depurar o aplicativo num ambiente controlado, e com o
mesmo código, rodá-lo num ambiente real mais tarde;
• SMPI: Foi criado para o estudo do comportamento de aplicações MPI no simu-

32
lador. O SMPI implementa as principais chamadas do MPI, não necessitando da
modificação do código fonte para realizar os testes no SimGrid;
• SimDag: Este módulo tem o objetivo de analisar o desempenho de heurísticas de
escalonamento descritas na forma de DAGs (Directed Acyclic Graphs).
Além das APIs, o SimGrid possui alguns módulos de suporte (XBT) e internos (SURF,
SIMIX e SMURF), brevemente explicados em seguida:
• SURF: Núcleo de simulação do SimGrid, é responsável pelos modelos matemáticos
da rede e CPU;
• SIMIX: Gerencia a execução dos processos do SimGrid;
• SMURF: Módulo em desenvolvimento que será responsável pela paralelização da
execução do simulador em diversas máquinas de forma a evitar problemas de esca-
labilidade em termos de memória;
• XBT: Módulo que oferece suporte aos demais, provendo estruturas de dados clás-
sicas, mecanismos de log e gerenciamento de exceções.
3.2.1 Núcleo de simulação
O núcleo de simulação do SimGrid implementa e fornece diversos modelos de simula-
ção que são usados nos diferentes tipos de recursos (rede, CPU, etc). O núcleo é composto
de 2 camadas principais, SURF e SIMIX, as quais são descritas com maiores detalhes em
seguida.
3.2.1.1 SIMIX
O SIMIX provê uma API baseada na biblioteca Pthread para o gerenciamento da
concorrência dos processos simulados. Precisamente, ele fornece as seguintes abstrações:
• Processos: Os processos do SIMIX correspondem aos fluxos de execução da apli-
cação simulada;
• Mutex: Usada para o controle do acesso às seções críticas pelos processos;
• Variáveis de condição: Usado para a sincronização e sinalização do término das
ações aos processos;
• Ações: Representam a utilização dos recursos pelas threads da aplicação simulada.
O funcionamento dessas abstrações pode ser ilustrado através de um simples exemplo.
Consideremos a simulação da computação de uma tarefa numa máquina. Essa computa-
ção está embutida num processo SIMIX e é iniciada através de uma chamada de uma API
do usuário, como por exemplo no caso do MSG, MSG_task_execute. A chamada
irá criar uma ação SIMIX correspondente à quantidade de cálculo a ser realizada (espe-
cificada pelo usuário através da chamada da função). Então, a ação é associada a uma
variável de condição na qual o processo é bloqueado. Uma vez que a ação termina, após
um tempo determinado pela simulação feita do recurso associado, a variável de condição
é sinalizada. Em seguida, o processo é desbloqueado e o controle retorna ao usuário que
irá continuar a execução de seu processo. O tempo simulado é, enfim, atualizado para
considerar a execução dessa tarefa.

33
LMM
SIMIX
SURF
MSG
Actions
(
372
435
245
245
530
530
50
664
work
remaining
variable
...
x1
x2
x2
x2
x3
x3
xn
+ +
+
... 6 CP
6 CL1
6 CL4
6 CL2
6 CL3



Constraints



































Variables
Conditions
{
... Process









u
s
e
r
c
o
d
e
u
s
e
r
c
o
d
e
u
s
e
r
c
o
d
e
u
s
e
r
c
o
d
e
u
s
e
r
c
o
d
e
...
Figura 3.2: Ilustrando a interação entre as camadas do SimGrid e as principais estruturas
de dados.
A maior parte das simulações consistem de diversos processos, os quais são execu-
tados em exclusão mútua e controlados pelo SIMIX. Basicamente, todos os processos
rodam em round-robin até que todos estejam bloqueados em variáveis de condições, es-
perando que as respectivas ações terminem. Portanto, num dado tempo de simulação t, o
SIMIX tem uma lista de processos bloqueados. Então, o SIMIX chama a camada inferior
(SURF), através da função surf_solve. O SURF, que será discutido em detalhes nas
próximas seções, é responsável pela manipulação do relógio da simulação e pelo uso dos
recursos. Assim, a função surf_solve avança o relógio da simulação para o tempo
t + δ, no qual ao menos uma das ações foi finalizada. Uma lista das ações completa-
das (com sucesso ou não) é, em seguida, retornada ao SIMIX. Após, o SIMIX acorda os
processos que estavam bloqueados nas ações terminadas. Esse procedimento é realizado
repetidas vezes, avançando o tempo de simulação conforme as tarefas são completadas,
até que todos os processos tenham terminado a sua execução e a aplicação do usuário seja
finalizada.
A execução da aplicação simulada é responsabilidade do SIMIX, ficando totalmente
separada da simulação da plataforma a qual é realizada pelo SURF. A comunicação entre
as camadas é feita inteiramente através das abstrações das variáveis de condições e das
ações, conforme mostrado na parte superior da Figura 3.2. Portanto, qualquer modificação
realizada no interior de cada camada é independente e transparente às demais.
3.2.1.2 SURF
O SURF provê diversos modelos para determinar os tempos de execução das ações
simuladas e o consumo dos recursos. Esses modelos podem ser selecionados e con-

34
figurados durante o tempo de execução do simulador, sendo cada modelo responsável
pelas ações de seu recurso (e.g., CPU, rede). Por exemplo, em termos dos modelos de
rede, a implementação atual fornece um modelo padrão para redes TCP (VELHO; LE-
GRAND, 2009), um modelo que repassa a simulação de rede para o simulador específico
GTNetS (RILEY, 2003), um modelo simples baseado em distribuições uniformes e mais
alguns modelos avançados para simular a rede, conforme (LOW, 2003). Com essas pos-
sibilidades, o usuário pode selecionar o modelo mais apropriado para seus fins, de acordo
com as necessidades de desempenho, precisão e escalabilidade, sem ser preciso modificar
o seu código fonte.
Todos os modelos são acessados através da função surf_solve que procede os
seguintes passos:
1. Consulta cada modelo de simulação ativo para obter a próxima data que uma ação
irá terminar (ou falhar).
Isso é feito através da função share_resources, a qual cada modelo deve im-
plementar. Para grande parte dos modelos, essa função utiliza uma camada extra,
chamada LMM, na qual o uso dos recursos é representado como um conjunto de
equações lineares (maiores detalhes são apresentados nas seções a seguir). Tal abor-
dagem permite representar situações extremamente complexas. O LMM usa uma
representação esparsa do sistema linear e utiliza, por padrão, uma simples aloca-
ção baseada no algoritmo max-min (BERTSEKAS; GALLAGER, 1992). Porém,
algoritmos mais sofisticados são implementados baseados no trabalho de (LOW,
2003).
Como visto na Figura 3.2, os modelos do SURF mantêm informações sobre a quan-
tidade restante de trabalho de cada ação e é capaz, portanto, de determinar quando
cada ação irá terminar baseada na atual simulação do uso dos recursos.
2. Calcula tmin, ou seja, a menor data de término entre todas as ações.
Em seguida, analisa os traços disponibilizados pelo usuário, os quais descrevem as
mudanças na disponibilidade dos recursos, para verificar se uma mudança ocorre
antes de tmin (e.g., a largura de banda disponível do link aumenta, ou uma máquina
é desligada). Se tal mudança no estado ocorre, a função update_resource_
state é chamada para atualizar o estado do recurso, sendo que cada modelo deve
implementá-la.
Finalmente, se necessário, tmin é atualizado para ser o menor tempo de mudança
dos recursos.
3. Solicita a cada modelo ativo para avançar o tempo de simulação em tmin, além de
atualizar o estado de cada ação conforme o necessário. Isso é feito através da função
update_action_state que cada modelo implementa.
4. Por fim, retorna o conjunto de ações que terminaram (ou falharam).
3.2.1.3 LMM
Grande parte dos modelos de simulação do SimGrid representam ações e recursos
como variáveis e restrições num sistema linear. Por exemplo, dado um conjunto de links
de rede L definido por suas larguras de banda e um conjunto de fluxos de rede F definido

35
pelos links utilizados nas comunicações, pode-se representar cada fluxo f como uma va-
riável xf (a qual representa a quantidade da largura de banda utilizada pelo fluxo). Para
cada link l, temos a seguinte restrição:
X
f∈l
xf 6 Cl, onde Cl é a largura de banda do link l,
A equação impõe que a largura de banda do link não seja excedida. Exemplificando, na
Figura 3.2, a variável x2 e x3 correspondem a 2 fluxos que usam os links {L1, L2, L3} e
{L2, L4}, respectivamente. Diversas alocações podem satisfazer o conjunto de restrições
das capacidades dos links e os protocolos de rede levam a diferentes alocações (LOW,
2003).
Em tais modelos, a camada LMM utiliza uma representação esparsa do sistema linear.
O problema é, então, resolvido pela função lmm_solve cuja complexidade é linear no
tamanho do sistema. O tamanho do sistema, por sua vez, depende do número de ações
e do número de recursos ativos. Por exemplo, o sistema correspondente ao conjunto de
N CPUs onde cada máquina roda uma ação, teria o tamanho Θ(N). Ainda, o sistema
correspondente a F fluxos utilizando L links teria o tamanho Θ(F.L).
Caso o sistema precise ser modificado, ele é invalidado e a alocação dos recursos
deve ser refeita, possivelmente agregando novas variáveis e restrições. Na Figura 3.2, por
exemplo, a remoção da variável x2 forçaria o novo cálculo da variável x3, enquanto a
remoção da variável x1 forçaria a nova alocação xn e assim por diante. De maneira gené-
rica, tais invalidações ocorrem baseadas no ciclo de vida das ações (criação, terminação,
suspensão, recomeço), ou seja, entre 2 chamadas sucessivas à função surf_solve ou
baseado na mudança dos recursos (i.e., quando a função update_resource_state
é chamada).
Os casos acima citados utilizam recursos de rede como recurso principal. Entre-
tanto, a mesma abordagem é válida para outros tipos de recursos, eventualmente mais
simples e menos desafiantes. A próxima seção analisa como a camada LMM é usada
na implementação do modelo de CPU padrão do SimGrid, detalhando como são imple-
mentadas as funções share_resources, update_resource_state e update_
action_state. O objetivo é apresentar rapidamente a complexidade de cada uma
dessas operações.
3.2.1.4 Modelo de CPU padrão
O modelo de CPU padrão tem seu próprio sistema LMM para evitar inoportunas e
desnecessárias invalidações por outros modelos. A cada CPU é associada uma restrição
cujo limite é o poder de processamento da CPU simulada (em MFlop/s). Abaixo, são
detalhados os principais componentes do modelo assim como suas complexidades:
Criação de ações: Uma ação é definida pela: quantidade restante de trabalho (em MFlop),
a qual é inicializada na criação da ação; e pela variável correspondente no sistema
LMM. A proporção na alocação dos recursos às ações varia ao longo do tempo. Por
exemplo, consideremos 2 ações A1 e A2 criadas para rodar numa CPU cujo poder
de processamento é C. Essa configuração será traduzida no nível do sistema LMM
como:
xA1 + xA2 6 C
O algoritmo de compartilhamento max-min determinará, em seguida, as seguintes
cotas:
xA1 = C/2

36
xA2 = C/2
A Figura 3.2 retrata a situação onde as variáveis x1 a xn correspondem a ações
sendo executadas num mesmo processador P. A ação xn, recentemente criada,
possui a mesma quantidade de trabalho restante e de trabalho total. Por outro lado,
a ação x1 foi criada num tempo passado.
share_resources: Para calcular a próxima data de terminação de uma ação, esta
função calcula uma nova solução do sistema LMM, caso necessário. Então, ela itera
sobre a lista de todas as ações ativas para calcular quando cada ação irá terminar,
baseado no compartilhamento atual dos recursos e a quantidade de trabalho restante
das ações, assumindo é claro, que o sistema se mantenha inalterado.
Portanto, a complexidade dessa função é Θ(|actions|) mais a complexidade da fun-
ção lmm_solve que também é Θ(|actions|).
update_resource_state: Toda vez que o estado de um recurso é alterado, é ne-
cessário atualizar a restrição correspondente cuja complexidade é Θ(1) e invalidar
o sistema LMM para recalcular o compartilhamento dos recursos.
update_action_state: Esta função avança o tempo simulado. Para isso, deve atu-
alizar a quantidade restante de trabalho de cada ação. Logo, o custo para iterar
sobre todas as ações é Θ(|actions|).
3.2.2 Análise de um simples caso de Computação Voluntária
Nesta seção é considerada uma plataforma com N máquinas cujos poderes de pro-
cessamento foram retirados dos traços disponíveis do projeto SETI@home (The Failure
Trace Archive, 2011). Em cada máquina um processo sequencialmente computa P tare-
fas cujas quantidades de trabalho são uniformemente amostradas no intervalo [0, 8.1012
]
(i.e., até aproximadamente 1 dia de cálculo numa máquina padrão). Este exemplo foi en-
viado por Eric Heien após ter utilizado o SimGrid no seu trabalho (HEIEN; FUJIMOTO;
HAGIHARA, 2008). Nas próximas seções, é analisada detalhadamente a complexidade
do SimGrid para rodar esse simples caso.
3.2.2.1 Inicialização do SimGrid
Durante a inicialização, um arquivo de plataforma, descrevendo as N máquinas, é
lido e as configurações são carregadas nas estruturas de dados correspondentes do SURF
e do LMM. Em seguida, o arquivo de deployment é lido, indicando em que máquina cada
processo irá executar. Com isso, os processos podem ser inicializados pelo SIMIX. Neste
caso, os processos rodam até a primeira chamada à função MSG_task_execute (para
executar uma tarefa na CPU), ponto no qual eles são bloqueados. No exemplo, todos os
processos são bloqueados a primeira vez no tempo simulado zero. A Figura 3.3 apresenta
as principais estruturas de dados criadas.
A complexidade geral da inicialização da simulação é Θ(N). Uma vez que cada
máquina é gerenciada independentemente, não é possível reduzir essa complexidade.
3.2.2.2 Primeira chamada à função surf_solve
Conforme descrito na Seção 3.2.1, quando todos os processos estão bloqueados, o
módulo SIMIX chama a função surf_solve. Como cada máquina roda apenas 1 tarefa
por vez, essa função aloca todo o poder computacional disponível para a ação que está

37
LMM
SURF
SIMIX
x1
x2
x3
6 C1
6 C2
6 C3
.
.
.
xN 6 CN



Constraints



































Variables
Actions
n
...
P1 P2 P3 PN
Conditions
{
Process
(
Figura 3.3: Estruturas de dados e camadas do SimGrid no simples caso de CV.
sendo executada (lmm_solve), calculando a data de término (share_resources) e
atualizando a quantidade restante de cálculo das demais (update_action_state).
Neste exemplo, o custo total da função surf_solve é Θ(N). Mais uma vez não é
possível diminuir o custo já que é necessário calcular as datas de término de todas as
ações.
3.2.2.3 Segunda chamada à função surf_solve
A primeira execução da função surf_solve, após atualizar seu relógio de simu-
lação, retorna as ações que acabaram de completar (ou falhar). Em geral, nesse caso,
há somente uma ação que acabou. Isso se deve ao fato dos tamanhos das tarefas serem
randômicos e as máquinas heterogêneas, sendo portanto, extremamente difícil que mais
de uma tarefa acabe ao mesmo tempo. Então, o SIMIX retorna o controle para o processo
do usuário correspondente, o qual destrói a ação que terminou. Em seguida, a função
MSG_task_execute retorna e é chamada novamente pelo processo para executar a
segunda tarefa da máquina. A nova ação é criada e o processo bloqueado mais uma vez.
Devido à nova tarefa, o sistema LMM correspondente ao modelo de CPU é invalidado e
o SIMIX chama a função surf_solve para determinar a próxima ação a terminar.
A complexidade entre as duas chamadas do SIMIX à função surf_solve é, por-
tanto, Θ(1) (apenas a criação/destruição da tarefa). Contudo, como o sistema é completa-
mente invalidado entre uma chamada e outra, a complexidade da função surf_solve
fica novamente em Θ(N) (resolução do sistema LMM), permanecendo assim para todas
as chamadas subsequentes, já que todo o sistema linear é sempre invalidado.
3.2.2.4 Discussão
Conforme as análises anteriores, toda vez que uma ação termina, toda a alocação dos
recursos é recalculada e todas as ações são atualizadas. Todavia, há somente uma pequena
modificação no sistema, causada pelo término de uma ação. Logo, quando essa ação
finaliza sua execução na máquina, ela não interfere nas datas de término das outras ações
rodando nas outras máquinas da plataforma. No exemplo ilustrado, quando a variável xi
é removida do sistema LMM, ela é imediatamente trocada por uma nova variável xi, a

38
qual sofre a mesma limitação de recurso da anterior.
Haverá, portanto, uma quantidade de chamadas à função surf_solve proporcional
ao número de tarefas na simulação. Como há N máquinas, cada uma executando P
tarefas, temos um total de NP ações. Consequentemente, a complexidade global do
SimGrid para rodar tal exemplo é Θ(N2
P). Como o número de máquinas em cenários
de Computação Voluntária tende a ser grande, uma complexidade quadrática pode tornar
inviável a simulação de tais ambientes.
Não obstante, no exemplo analisado, o poder computacional das máquinas se mantém
constante ao longo do tempo. Assume-se que cada máquina é anotada com um arquivo de
traço com T eventos de mudança de estado, onde cada mudança ocasionaria a atualização
do poder computacional disponível para aquela máquina. Neste caso, haveria um total de
NT eventos de mudança de estado. Ainda, o tempo necessário para recuperar um evento
seria Θ(log N) (considerando o uso de uma estrutura do tipo heap para o armazenamento
do próximo evento de cada recurso), o qual é desprezível quando comparado às chamadas
à função surf_solve. Conclui-se, então, que a complexidade global no caso do exem-
plo estudado com arquivos de traços seria Θ(N2
(P + T)), a qual é inaceitavelmente alta
para valores grandes de N e T.
3.2.3 Melhorias propostas
Nesta seção são propostas soluções para os problemas levantados nas seções anterio-
res. A primeira melhoria remove o recálculo desnecessário do sistema LMM entre duas
chamadas sucessivas à surf_solve (Seção 3.2.3.1). Essa melhoria é efetiva apenas
quando combinada com um melhor gerenciamento das ações (Seção 3.2.3.2). Ambas me-
lhorias são genéricas e podem ser usadas tanto nos modelos de CPU quanto nos modelos
de rede do núcleo de simulação do SimGrid. Ainda, é proposta uma terceira modifica-
ção que é aplicável às máquinas cuja disponibilidade da CPU varie ao longo do tempo
(Seção 3.2.3.3).
É importante ressaltar que nenhuma das melhorias propostas altera a qualidade da si-
mulação do SimGrid. O compartilhamento dos recursos entre as tarefas é exatamente o
mesmo entre todos os modelos de CPU utilizados. Este era um dos requisitos básicos na
proposição das modificações, de forma a tornar totalmente transparente ao usuário o mo-
delo de CPU que está sendo utilizado. O correto funcionamento foi comprovado através
de uma série de testes de regressão automatizados existentes na distribuição do SimGrid.
Através deles, viu-se que os tempos simulados eram os mesmos independentemente do
modelo de CPU escolhido. Além disso, todas as melhorias foram adicionadas na raiz
principal do código fonte do SimGrid e estão disponíveis na versão atual (3.5).
3.2.3.1 Invalidação parcial do sistema LMM
No exemplo descrito na Seção 3.2.2, o sistema LMM é invalidado entre cada chamada
à surf_solve, obrigando a resolução completa do sistema LMM mesmo quando ape-
nas algumas variáveis são modificadas. Temos que duas variáveis x e y interferem uma
à outra (denotado por x ∼ y), se existe um fecho transitivo de ∼. Entre duas chamadas
à função lmm_solve, é necessário apenas recalcular todas as variáveis pertencentes às
classes de equivalência das variáveis que foram adicionadas ou removidas.
A primeira melhoria realizada é calcular durante a execução o fecho transitivo acima,
de forma a recalcular somente as variáveis que são estritamente necessárias. Usando a
representação esparsa do sistema, combinada com o uso conjunto de estruturas de dados
eficientes, a complexidade da invalidação é linear no tamanho dos componentes conecta-

39
dos, sendo portanto, a complexidade ótima para esse caso.
No exemplo analisado anteriormente, apenas uma variável precisa ser recalculada e o
custo de lmm_solve é Θ(1) (comparado com o antigo custo de Θ(N)). Essa otimização
também é aplicada para o caso do sistema linear tal como o usado nos modelos de rede.
Nota-se que quando a interação entre as variáveis é mais complexa, pode ser necessário
recalcular todo o sistema linear. Nesse caso pessimista, a complexidade é ainda linear no
tamanho do sistema, isto é, possui a mesma ordem de complexidade que sem o mecanismo
de invalidação parcial.
3.2.3.2 Gerenciamento preguiçoso das ações
A invalidação parcial do sistema LMM torna possível reduzir a complexidade da fun-
ção lmm_solve. Porém o custo da share_resources ainda é Θ(|actions|), uma vez
que a data de término de cada ação é recalculada após cada chamada à lmm_solve. To-
davia, apenas as ações cujo compartilhamento do recurso foi alterado pelo lmm_solve
precisam ser atualizadas.
Introduz-se, então, um conjunto de eventos futuros, implementados utilizando a estru-
tura de dados heap, na qual é armazenada a data de término das diferentes ações. Quando
o compartilhamento de um recurso é alterado, todas as ações correspondentes, i.e., que
utilizam esse recurso, são removidas do conjunto. Então, a data de término de cada ação é
atualizada e a ação reinserida no heap. A complexidade para inserir e remover elementos
no heap é Θ(log(|actions|)), enquanto o custo de calcular a menor data de término entre
as ações do sistema é apenas O(1).
A última função custosa é a update_action_state. Essa função deve atualizar
o estado de todas as ações do sistema, principalmente a quantidade restante de trabalho,
e retornar o conjunto de ações que terminaram e falharam. Portanto, não há nenhuma
possibilidade de reduzir essa complexidade de Θ(|actions|) caso se mantenha a restrição
de manter todas as tarefas atualizadas. Por isso, propõe-se a atualização do restante das
ações de forma preguiçosa. Mais precisamente, a atualização preguiçosa consiste em
atualizar o restante de trabalho apenas quando necessário para recalcular a data de término
das tarefas ou quando esse valor for requisitado por uma API de nível de usuário (e.g.,
MSG). Na função update_action_state é apenas removida a tarefa finalizada do
conjunto de eventos futuros, de forma a permitir a redução da complexidade do update_
action_state para Θ(log(|actions|)).
No exemplo analisado, a complexidade da função surf_solve é, portanto, Θ(log N)
e a complexidade geral da simulação é Θ(NP. log(N)) ao invés de Θ(N2
P).
Por outro lado, num exemplo mais complexo onde a data de término da maioria
das ações precise ser atualizada, o novo algoritmo pode ser mais lento que o anterior
(Θ(|actions|. log(|actions|) ao invés de Θ(|actions|)). Contudo, as melhorias propostas
devem ser benéficas na maior parte das situações, uma vez que apenas algumas ações
são alteradas em cada passo da simulação. Além disso, o usuário pode desativá-las caso
necessário.
3.2.3.3 Integração dos traços
Nesta seção é analisado o caso em que os recursos de CPU possuem traços associados.
A cada evento de traço, é chamada a função update_resource_state, a qual leva
ao recálculo do compartilhamento do recurso correspondente durante a próxima execução
da função surf_solve. Isto é inevitável no caso da simulação de situações complexas
como a rede, mas quando os recursos são independentes e não interferem uns nos outros,

40
podemos evitá-lo.
Considere uma CPU qualquer cujo poder computacional no instante t seja denotado
por p(t). Defini-se a quantidade de trabalho realizado num período de tempo como:
P(x) =
Z x
0
p(t).dt.
Considere n ações, A1, . . . , An, rodando nesta CPU, cada uma com a quantidade restante
de trabalho (em MFlop) Ri no instante t0. Em qualquer instante t > t0, cada ação recebe
uma fatia do poder computacional da CPU igual a p(t)/n. Portanto, durante o intervalo
de tempo [a, b], a ação Ai irá avançar em
R b
a
p(t)/n.dt = 1/n
R b
a
p(t).dt.
O valor retornado pela função share_resources é o maior t1 tal que 1/n
R t1
t0
p(t).dt 6
Ri, i.e., t1 é tal que: Z t1
t0
p(t).dt = n min Ri.
Dessa forma, obtém-se o tempo t1 no qual a menor das tarefas terá acabado.
Através da pré-integração do traço, t1 pode ser calculado usando uma simples busca
binária. O tempo necessário para realizar a pré-integração do traço é igual ao tempo de
leitura do mesmo (ao invés de armazenar o traço p, é gravada a integral P como somas
cumulativas dos valores). O custo de encontrar t1 é, portanto, logarítmica no tamanho do
traço.
No exemplo simples de Computação Voluntária analisado, o compartilhamento pre-
cisa ser recalculado apenas para uma máquina a cada chamada à surf_solve e o custo
da função share_resources é, logo, somente Θ(log(T) + log(N)), quando combi-
nado com a melhoria do gerenciamento preguiçoso das ações. Por isso, a complexidade
geral da simulação é Θ(NP(log(N)+log(T))), em vez de Θ(N2
(P +T)) sem nenhuma
melhoria ou Θ(N(P + T) log(N)) com a invalidação parcial do sistema LMM e o geren-
ciamento preguiçoso das ações.
Nota-se que ao contrário das melhorias descritas nas seções anteriores, esta apenas
funciona para os recursos de CPU. Entretanto, ela é fundamental para as simulações de
CV, uma vez que a disponibilidade das máquinas é frequentemente descrita através de
grandes arquivos de traços.
3.2.4 Avaliação de desempenho
Nesta seção são apresentados os resultados de dois diferentes experimentos com o
objetivo de verificar a efetividade das melhorias feitas no núcleo do SimGrid. Na Se-
ção 3.2.4.1 é medido o tempo necessário para uma simulação do exemplo ilustrado na
Seção 3.2.2. Na Seção 3.2.4.2, é apresentado o resultado da comparação de um simula-
dor BOINC implementado com o SimGrid com dois simuladores do BOINC existentes,
o BOINC Client Simulator e o SimBA.
3.2.4.1 Estudo do simples exemplo de aplicação de CV
Para esse estudo foi considerada uma plataforma simples com N máquinas cujos po-
deres de processamento foram retirados de máquinas reais do projeto SETI@home (The
Failure Trace Archive, 2011). No primeiro experimento, as máquinas estão disponíveis
durante todo o tempo de simulação, enquanto no segundo, são usados os arquivos de
disponibilidade do SETI@home. Em cada máquina, um processo worker processa, se-
quencialmente, tarefas cujo tamanho é uniformemente amostrado no intervalo [0, 8.1012
]
(i.e., até um dia de processamento numa máquina padrão).

41
Número de Máquinas Simuladas
Tempo
de
Execução
(s)
1
2
8
0
2
5
6
0
5
1
2
0
1
0
2
4
0
0.001
0.01
0.1
1
10
100
1000
10000
100000
1
0
2
0
4
0
8
0
1
6
0
3
2
0
6
4
0
Modelo de CPU padrão
Invalidação parcial LMM
Gerenciamento preguiçoso
Integração dos traços
Figura 3.4: Tempo de execução vs. número de máquinas simuladas usando as diferentes
melhorias propostas (usando uma escala logarítmica em ambos os eixos).
Os tempos reportados nesta seção foram obtidos num AMD Opteron 248 Dual Core
(2.2 GHz) com 1MB de cache L2 e 2 GB de memória RAM. Os experimentos foram
rodados ao menos 10 vezes e o intervalo de confiança de 95%, baseado na distribuição de
Student, é plotado em todos os gráficos (apesar de na maioria dos casos, devido à escala
logarítmica, ser difícil de notar o intervalo de confiança).
Nos testes foram comparadas quatro versões do SimGrid:
• Modelo de CPU padrão: Versão original da implementação do modelo de CPU
utilizado no SimGrid, conforme descrita nas Seções 3.2.1 e 3.2.2;
• Invalidação parcial do sistema LMM: como acima, porém usando a melhoria des-
crita na Seção 3.2.3.1;
• Gerenciamento preguiçoso das ações: como acima, porém usando a melhoria des-
crita na Seção 3.2.3.2;
• Integração dos traços: usando a melhoria proposta na Seção 3.2.3.3.
Experimentos sem traços
Nestes experimentos o número de máquinas, N, varia de 10 a 10240, uma semana
de computação é simulada e nenhum arquivo de traço de disponibilidade é usado. A
Figura 3.4 apresenta o tempo de execução em função do N utilizado para as 4 versões do
SimGrid analisadas.
Conforme o esperado, a invalidação parcial do sistema LMM melhora, significante-
mente, o desempenho quando comparado ao modelo padrão. Entretanto, a complexidade
assintótica de ambas as implementações é similar no senso que o cerne do custo é o com-
ponente N2
da complexidade O(N2
P). Isto pode ser visto na inclinação das duas curvas.
Nota-se que para estes dois casos a simulação foi limitada a 2560 máquinas devido ao

42
0.001
0.01
0.1
1
10
100
1000
10000
100000
1
0
2
0
4
0
8
0
1
6
0
3
2
0
6
4
0
1
2
8
0
2
5
6
0
5
1
2
0
1
0
2
4
0
Tempo
de
Execução
(s)
Número de Máquinas Simuladas
Modelo de CPU padrão
Invalidação parcial LMM
Gerenciamento preguiçoso
Integração dos traços
Figura 3.5: Tempo de execução vs. número de máquinas simuladas usando as diferentes
melhorias propostas (usando uma escala logarítmica em ambos os eixos).
tempo de execução extremamente longo (e.g., 16 horas para 5120 máquinas com o mo-
delo padrão de CPU).
As outras 2 versões do SimGrid escalam significantemente melhor graças a sua menor
complexidade O(NP log(N)). Ambas possuem desempenho similar por não terem sido
usados arquivos de disponibilidade, com os quais a versão com integração dos traços é
mais eficiente. Com as novas versões, é possível simular 1 semana de computação com
10240 máquinas em aproximadamente 1 minuto.
Experimentos com traços
A Figura 3.5 mostra os resultados para os experimentos com arquivos de disponibili-
dade das máquinas do projeto SETI@home. Esses traços são disponibilizados pelo Fai-
lure Trace Archive (The Failure Trace Archive, 2011) e seu tamanho total varia de 148KB
para 10 máquinas até 177MB para 10240 máquinas. Logo, o tempo de processamento dos
traços se torna uma parte substancial dos tempos de execução (aproximadamente um terço
quando é usada a integração do traço).
Os resultados para os modelos padrão e invalidação parcial do sistema LMM são limi-
tados a 2560 máquinas por causa dos problemas de escalabilidade. Pelo mesmo motivo,
os resultados do gerenciamento preguiçoso das ações é limitado a 5120 máquinas. De
fato, o gerenciamento preguiçoso não é suficiente para atingir uma boa escalabilidade
quando são utilizados arquivos de traço. Isto é causado pela complexidade linear no nú-
mero de eventos de traço, i.e., O(N(P + T) log(N)). A integração dos traços, por sua
vez, reduz essa complexidade para O(NP(log(N) + log(T))), o que explica seu melhor
desempenho.
A última versão proposta é, portanto, a melhor escolha para a simulação de ambientes
de Computação Voluntária. Através dela, foi possível rodar as simulações com traços tão
rapidamente quanto no caso sem os arquivos de disponibilidade.

43
Projeto Tempo de processamento (horas) Deadline (dias)
Einstein 24 14
SETI 1.5 4.3
LHC 1 4
Tabela 3.1: Características dos projetos BOINC
0.01
0.1
1
10
100
1000
1e+06 1e+07 1e+08 1e+09
Tempo
de
Execução
(s)
Tempo de Simulação (s)
BOINC Client Simulator
SimGrid
Figura 3.6: Comparação do tempo de execução entre o BOINC Client Simulator e o
SimGrid.
3.2.4.2 Estudo de um aplicativo tipo BOINC
Como prova de conceito da capacidade do SimGrid simular sistemas de CV, foi im-
plementado um simulador para a arquitetura BOINC (maiores detalhes na Seção 3.3).
O simulador implementa as principais funcionalidades da política de escalonamento do
cliente, como descrito em (ANDERSON; MCLEOD VII, 2007).
A seguir é comparado o simulador construído em cima do SimGrid com o BOINC
Client Simulator que permite a simulação de um cliente BOINC. Em seguida, é feita a
comparação com o SimBA. Para isso, os testes foram conduzidos numa máquina similar
àquela usada no trabalho (TAUFER et al., 2007), um Intel Pentium 4 3.0GHz com 1GB
RAM, de forma que os tempos de execução medidos possam ser comparados de maneira
justa com o SimBA.
Para todos os experimentos, foi usado o SimGrid com todas as melhorias descritas na
Seção 3.2.3, usando um modelo de rede simples baseado em distribuições uniformes.
Comparação com o BOINC Client Simulator
Foram simulados 3 conhecidos projetos do BOINC: Einstein@home, SETI@home e
LHC@home. A Tabela 3.1 apresenta os tempos para processar cada tarefa dos projetos,
além dos prazos de término impostos por ele, conforme retirado do catálogo de projetos
ativos do BOINC 1
.
Em termos de tempos de execução, como mostrado na Figura 3.6, o SimGrid se mos-
trou mais rápido que o BOINC Client Simulator, apesar do último ser construído com
o fim específico de simular um cliente e sua simulação avançar em passos de tempo
predefinidos. Por todas essas razões, esperava-se que o BOINC Client Simulator fosse
1
http://www.boinc-wiki.info/Catalog_of_BOINC_Powered_Projects

44
extremamente eficaz e consequentemente mais veloz que o SimGrid.
Comparação com o SimBA
Para os resultados desta seção, configurou-se o SimGrid para que a pilha usada para
simular os processos fosse reduzida do padrão 128KB para 16KB. Essa medida foi ne-
cessária para que a simulação pudesse rodar sem problemas numa máquina com 1GB de
RAM. Os tempos de execução medidos com o SimGrid e aqueles reportados por Estrada
et al. no trabalho (TAUFER et al., 2007) são comparados da seguinte forma:
• O SimBA simulou 15 dias de cálculo com 7810 máquinas trabalhando para o pro-
jeto Predictor@home em 107 minutos. O SimGrid simulou a mesma configuração
em menos de 4 minutos (cada teste foi executado 10 vezes e o intervalo de confiança
de 95% ficou entre [208.13, 223.71] segundos);
• 8 dias de cálculo com 5093 clientes trabalhando para o projeto CHARMM foram
simulados em 44 minutos no simulador SimBA. Já no SimGrid, o teste demorou
menos de 1.5 minutos (cada teste com 10 execuções e intervalo de confiança de 95%
entre [80.38, 80.87] segundos). Nota-se que, em ambos os experimentos, foram
utilizados os traços de disponibilidade do projeto SETI@home e aproximadamente
um terço do tempo de simulação foi gasto para ler esses arquivos.
Normalmente, o esperado seria que o simulador do BOINC implementado sobre o
SimGrid não fosse "muito lento" quando comparado com o SimBA, mas ao contrário
ele foi mais rápido. Isto porque o SimBA opta por diversas soluções simplísticas para
alcançar uma boa escalabilidade, tais como o uso de máquina de estado finito e distribui-
ções estatísticas para simular a disponibilidade das máquinas. Ao contrário, o SimGrid
opta por usar opções mais sofisticadas porém custosas, tais como a execução de código
arbitrário para os processos e o uso de traços reais de disponibilidade. Como resultado,
temos que a construção de um simulador de CV com o SimGrid proporciona a princi-
pal vantagem que é poder ser facilmente programável e estendido. Por exemplo, novas
políticas de escalonamento podem ser implementadas de maneira simples usando a API
MSG. Outra opção é o estudo da comunicação através da ativação de algum modelo de
rede mais complexo. Além disso, seria possível simular diferentes conjuntos de traços de
disponibilidade e verificar o desempenho do sistema. Por fim, o estudo de políticas de
escalonamento do servidor, frente a um cenário com múltiplos projetos e clientes, poderia
ser implementado e realizado.
3.3 Simulador do BOINC proposto
Esta seção descreve as principais decisões tomadas para a criação do simulador do
BOINC proposto, de forma a obter um aplicativo que fosse capaz de simular o comporta-
mento do ambiente de maneira confiável. O código foi desenvolvido em C, utilizando a
API MSG do SimGrid. Composto de aproximadamente 2500 linhas de código, é dividido
em 2 elementos principais: o cliente que é o responsável por representar o funcionamento
dos usuários do BOINC e foi baseado no comportamento descrito em (ANDERSON;
MCLEOD VII, 2007); e o servidor, responsável por distribuir as tarefas ao conjunto de
clientes.
Cliente: As principais funcionalidades do cliente foram implementadas, tais como:

45
• Políticas de escalonamento: A seleção das tarefas a rodarem na CPU segue as
noções de débito e urgência (EDF) descritas no artigo;
• Políticas de requisição de tarefas: Implementaram-se os mecanismos que ga-
rantem a equidade no longo prazo entre os projetos;
• Prioridade dos projetos: Cada cliente pode selecionar a prioridade desejada a
cada projeto;
• Intervalo de escalonamento e conexão: Entre os parâmetros do cliente foram
incluídos a fatia padrão de tempo que uma tarefa roda na CPU e o intervalo
padrão entre conexões aos servidores dos projetos.
Servidor: Já do lado do servidor, optou-se por implementar os elementos fundamentais
na distribuição e controle das tarefas, entre eles:
• Quorum: Foi implementado um mecanismo que controla o número mínimo
de tarefas completadas, reenviando as tarefas caso necessário;
• Deadline: O prazo de término de cada tarefa é controlado individualmente,
replicando-a em outra máquina caso esta perca seu prazo;
• Políticas de escalonamento: Foram implementadas as 3 políticas de escalo-
namento citadas na Seção 2.2.2 (Fixa, Saturação e EDF), as quais podem ser
ativadas ou desativadas conforme a necessidade de simulação;
• Intervalo entre rajadas: Para os projetos em rajadas, é possível determinar,
além da quantidade de tarefas, o intervalo de tempo em que a rajada está dis-
ponível;
• Número de réplicas: Determina quantas unidades de cada tarefa são distribuí-
das aos clientes. É garantido que cada cliente recebe uma única cópia de cada
tarefa;
• Replicação adaptativa: Implementou-se o mecanismo de replicação adapta-
tiva, conforme descrito na Seção 2.2.2.
Devido à complexidade do ambiente BOINC, seria extremamente difícil de modelar
todos os elementos. Entre as principais restrições do sistema, podemos citar:
• Nenhuma restrição é feita sobre configuração da máquina cliente (quantidade de
memória RAM, disco, sistema operacional, etc). Logo, todas as tarefas dos projetos
podem rodar em todos os clientes;
• O checkpoint das tarefas não é completamente modelado. A abordagem realizada
consiste na continuação da tarefa do ponto onde ela parou caso a máquina do cliente
fique indisponível, independentemente das características do projeto;
• O mecanismo de crédito não foi implementado. Dessa forma, não é contada a
quantidade de crédito que cada cliente tem direito. Entretanto, as políticas se esca-
lonamento implementadas garantem o necessário para otimizar o crédito ganho (os
recursos são usados o máximo possível).

46
Tempo SimGrid BOINC Client Simulator
(horas) Einstein SETI LHC Einstein SETI LHC
100 1 23 27 1 21 33
500 7 112 163 7 108 166
1000 12 220 272 14 220 331
5000 70 1106 1565 70 1103 1652
10000 139 2221 3327 139 2214 3319
Tabela 3.2: Número de tarefas completadas para o SimGrid e o BOINC Client Simulator.
3.3.1 Validação
Com o intuito de verificar que as políticas de escalonamento e solicitação dos clientes
foram implementadas corretamente e são fiéis ao comportamento real do sistema, foi
realizada uma comparação do simulador proposto com o BOINC Client Simulator. O
BOINC Client Simulator simula o comportamento de um cliente interagindo com vários
servidores BOINC. Por utilizar o próprio código fonte, podemos considerá-lo fiel ao seu
comportamento.
A validação do cliente BOINC é importante uma vez que esses elementos serão fixos
nos nossos experimentos, ou seja, serão variados somente os parâmetros do servidor para
verificar o impacto dessas modificações no sistema como um todo. Assim, possíveis
injustiças no nível de escalonamento do cliente poderiam repercutir no desempenho dos
demais elementos do sistema.
Para realizar esse experimentos foram utilizados os mesmos parâmetros do teste des-
crito na Seção 3.2.4.2. Naquele teste foram simulados 3 projetos do BOINC (Eins-
tein@home, SETI@home e LHC@home) e a Tabela 3.1 apresenta as características das
tarefas.
A Tabela 3.2 apresenta o número de tarefas completadas para cada projeto num dado
intervalo de tempo que varia de 100 até 10000 horas. Em todos os experimentos, inde-
pendente do simulador, nenhuma tarefa perdeu seu prazo de término. Mais relevante é
que mesmo para períodos extremamente longos, o número de tarefas completas é bem
próximo nos dois simuladores. O experimento realizado pode não ser suficiente para a
completa validação do simulador proposto, porém ele permite concluir que o simulador é
capaz de, em linhas gerais, se assemelhar ao comportamento de um cliente real.
Neste capítulo foi apresentada a ferramenta utilizada para a condução do estudo reali-
zado nesta dissertação. Inicialmente, viu-se os fatores que são importantes na simulação
de sistemas de CV e os motivos que levaram a escolha do simulador SimGrid, tais como
o uso de código genérico para os processos e o uso de arquivos de traços para modelar a
volatilidade dos clientes. Contudo, o SimGrid possuía sérios problemas de desempenho
que inviabilizariam a realização dos experimentos previstos.
Em seguida, descreveu-se o funcionamento interno do SimGrid de forma a descobrir
qual era o gargalo de desempenho do mesmo. Foram propostas e implementadas três
melhorias para o modelo de CPU do simulador: a invalidação parcial do sistema LMM,
o gerenciamento preguiçoso das ações e a integração dos traços de disponibilidade das
máquinas. Através da avaliação de desempenho realizada, foi possível ver o ganho obtido
e concluir que os novos modelos são eficazes para os ambientes de CV. Ainda, verificou-se

47
com a realização dos testes de regressão que a qualidade da simulação não foi alterada.
Por fim, apresentou-se as decisões de design tomadas durante a construção do simu-
lador do BOINC utilizado, mostrando quais os elementos do sistema foram modelados
e quais não foram considerados nesse estudo. Uma breve avaliação do nosso simula-
dor também foi realizada, comparando-o a dois simuladores do BOINC já existentes, o
BOINC Client Simulator e o SimBA. Concluiu-se que os resultados, em linhas gerais,
foram próximos daqueles esperados e que o simulador pode ser utilizado para o restante
do trabalho.

49
4 NOTAÇÃO TEÓRICA DO JOGO
Este capítulo apresenta a notação teórica adotada para modelar os elementos com-
ponentes das plataformas de CV. São modelados os dois principais atores do ambiente,
os servidores dos projetos e os clientes. Além disso, são vistas as estratégias possíveis
aos jogadores e as métricas que são utilizadas para analisar e comparar o desempenho do
sistema.
Um sistema de Computação Voluntária, tal qual o BOINC, consiste de voluntários
que oferecem seus recursos para serem compartilhados entre um conjunto de projetos. Os
mecanismos de escalonamento por trás do sistema devem garantir uma divisão eficiente e
justa dos recursos. Entretanto, diversos parâmetros de configuração do ambiente podem
afetar esse compartilhamento. A seguir, é explicado como esta situação (diversos projetos
compartilhando recursos de clientes) pode ser modelada através do uso de noções de teoria
dos jogos. Primeiramente, são definidos os principais atores do sistema: voluntários e
projetos.
Definição 1 (Voluntário Vj). Um voluntário BOINC é caracterizado pelos seguintes pa-
râmetros:
• Um desempenho máximo (em MFLOP.s−1
) indicando a quantidade de MFLOP
que ele pode processar por segundo quando está disponível;
• Um traço de disponibilidade, i.e., uma sequência ordenada de tempos disjuntos
que indicam quando a máquina de um voluntário está disponível. Esse traço é des-
conhecido pelo escalonador do cliente voluntário, o qual também não usa nenhuma
informação histórica sobre o mesmo para obter um melhor escalonamento;
• A fatia de compartilhamento dos projetos, i.e., a lista de projetos para qual o
voluntário está pronto para trabalhar e qual prioridade foi configurada para cada
projeto.
Uma coleção de voluntários é denotada por V.
Nesta modelagem, os voluntários foram considerados como passivos e apenas prove-
dores de recursos. Mais tarde, será visto como examinar a satisfação dos usuários, porém
neste estudo, eles são considerados completamente passivos.
Define-se, agora, as principais características dos projetos do BOINC.
Definição 2 (Projeto Pi). Um projeto BOINC é caracterizado pelos seguintes parâmetros:
• wi [MFLOP.tarefa−1
] denota o tamanho de uma tarefa, i.e., a quantidade de
MFLOP necessária para realizar uma tarefa. Assume-se que o tamanho da tarefa

50
do Pi é uniforme. Claramente, isto é uma aproximação, porém ela geralmente se
mantém verdadeira para muitos projetos numa escala de tempo de algumas sema-
nas 1
;
• bi [tarefa.lote−1
] denota o número de tarefas de cada lote. Novamente, assume-
se que todos os lotes possuem o mesmo tamanho. Essa aproximação pode não ser
realística para projetos do tipo GridBOT (SILBERSTEIN et al., 2009). Contudo,
consideramos que essa abordagem é razoável neste primeiro estudo. Ainda, como
não estamos interessados em como um determinado projeto pode priorizar suas
rajadas, ela não deve afetar nossas conclusões;
• ri [lote.dia−1
] denota a taxa de entrada, i.e., o número de lotes de tarefas por dia.
Mais um vez, assume-se este valor como fixo e não são considerados os potenci-
ais períodos sem tarefas que podem acontecer na escala de semanas ou meses de
simulação.
Ainda, considera-se que ri, bi e wi são tais que não saturam completamente o sis-
tema, isto é, tais que um lote sempre termine antes da submissão de um novo. De
fato, como foi explicado anteriormente, não estamos interessados como um de-
terminado projeto pode priorizar seus lotes, mas sim, como os diferentes projetos
podem interferir uns aos outros. Logo, os pressupostos acima não devem ser preju-
diciais nesse contexto;
• Obji é a função objetiva do projeto. Dependendo da natureza de cada projeto, ela
pode ser o throughput %i, i.e., o número médio de tarefas processadas por dia, ou
o tempo médio de término de um lote αi;
• qi é o quorum, i.e., o número de resultados processados com sucesso que precisam
ser retornados ao servidor antes que a tarefa possa ser considerada válida. Nos
nossos experimentos, foi assumido que o qi é sempre igual a 1 tarefa.
Um projeto Pi é portanto uma tupla (wi, bi, ri, Obji) e uma instância do sistema é, logo,
uma coleção de projetos P = (P1, . . . , PK). O conjunto de todas essas possibilidades de
instâncias de projetos é denotado por P.
Usando a terminologia da teoria dos jogos, os projetos serão referidos como jogado-
res. Na mesma linha, o termo estratégia é usado para se referir ao conjunto de opções
de "jogadas" que os jogadores possuem e que podem influenciar o compartilhamento dos
recursos disponíveis.
Definição 3 (Estratégia Si). O servidor de cada projeto pode ser configurado com valo-
res específicos que influenciam diretamente seu desempenho. Neste estudo, foca-se nos
seguintes parâmetros:
• πi é a política de envio de tarefas (KONDO; ANDERSON; MCLEOD, 2007)
usada pelo servidor quando da recepção de uma requisição de trabalho. Quando
um cliente conecta-se ao servidor, ele demanda por tarefas suficientes para mantê-
lo ocupado por um período de tempo determinado (e.g., um dia). Então, o servidor
é responsável por determinar quantas e quais tarefas serão enviadas.
1
http://www.boinc-wiki.info/Catalog_of_BOINC_Powered_Projects

51
A estratégia mais simples πcste = c envia uma quantidade fixa (c) de tarefas, não
importando qual é o estado do cliente e do servidor. Nessa estratégia mais sim-
ples, c poderia ser determinado pela duração média das tarefas e pela quantidade de
trabalho requisitada. Políticas de envio de tarefas mais elaboradas como saturação
(πsat) e EDF (πEDF ) foram introduzidas na Seção 2.2.2;
• σi é o slack (KONDO; ANDERSON; MCLEOD, 2007). Esse valor é usado para
determinar o prazo de término atribuído para as tarefas no momento da submissão
aos clientes. Por exemplo, se o tempo médio de cálculo de uma tarefa numa má-
quina de referência, de uso dedicado à tarefa, é uma hora, então um slack de 2 iria
resultar num prazo de término de 2 horas. A mais simples das estratégias, σcste = s,
significa que um slack de s é usado. Na prática, estratégias mais elaboradas, como
adaptar o slack conforme a velocidade/disponibilidade/confiabilidade da máquina
do voluntário ou ainda, ao progresso do lote, poderiam ser usados mas este estudo
não explora tais possibilidades;
• τi é o intervalo de conexão (HEIEN; ANDERSON; HAGIHARA, 2009) e indica
aos clientes o quão frequente eles devem tentar se reconectar ao servidor. Esse
parâmetro influencia com qual rapidez os voluntários irão perceber e reagir às novas
tarefas que precisam ser processadas num projeto em rajadas. Nos experimentos,
este parâmetro varia no intervalo de 12 minutos até 30 horas;
• γi é a estratégia de replicação (KONDO; CHIEN; CASANOVA, 2007). A estraté-
gia de replicação tratada neste item é completamente diferente da replicação usada
para alcançar um determinado quorum mínimo. γi é usada para evitar que uma
máquina lenta seja o gargalo do sistema e atrase o término de um lote. Portanto, a
estratégia γcste = r permite submeter no máximo r réplicas de uma mesma tarefa
cujos prazos de término não tenham expirado. Novamente, estratégias mais esper-
tas que se adaptem à confiabilidade dos voluntários e ao progresso do lote poderiam
ser usadas. Entretanto, neste estudo não são exploradas tais possibilidades.
A estratégia Si de um projeto Pi é, logo, uma tupla (πi, σi, τi, γi) e o conjunto de todas
as possíveis estratégias para todos os projetos é denotada por S.
Definição 4 (Resultado (Outcome) O). Uma vez que um conjunto de projetos P decidiu
por uma certa estratégia S, os recursos do conjunto de voluntários V são compartilhados
através dos mecanismos de escalonamento do BOINC.
O resultado O(V, P, S) é o conjunto de todas as informações sobre o término das
tarefas e lotes dos diferentes projetos. No restante do trabalho, quando necessário, deno-
taremos por Oi a informação de O restrita ao projeto Pi.
A partir desse resultado, pode-se calcular os seguintes valores:
• Throughput dos projetos contínuos. Se Pi é um projeto contínuo (ou seja, possui
continuamente um grande número de tarefas), pode-se, então, computar o número
total de tarefas do Pi que foram processadas num período de tempo;
• Tempo médio de término de um lote. Se o Pi é um projeto em rajada, então
podemos calcular a soma do tempo necessário para completar cada lote (contando
o tempo de sua chegada ao sistema até a data do término da sua última tarefa) e
calcular a média do número total de lotes que foram submetidos ao longo de um
determinado período;

52
• Perda, Waste. Por vezes, as tarefas não conseguem ser finalizadas antes de seus
prazos de término. Isto pode ocorrer por causa da máquina do voluntário que era
muito lenta, ou porque ela ficou indisponível por um longo período, ou ainda, por-
que o slack do projeto era muito curto.
Em tais casos, a tarefa é normalmente reenviada a outro cliente e o primeiro, pos-
sivelmente, não receberá nenhum crédito por ela. Logo, o tempo gasto trabalhando
em tarefas perdidas, ou seja, que passaram seu prazo de término, é desperdiçado
tanto no ponto de vista do cliente (que perdeu seu crédito), quando do servidor (que
enviou a mesma tarefa a outro voluntário).
Para um determinado projeto Pi e um determinado voluntário Vj, denota-se a perda
por Wi,j, a divisão do número de tarefas do Pi perdidas por Vj pelo total de tarefas
que ele recebeu do projeto Pi.
Da mesma forma, a perda do Pi denota a divisão entre o número total de tarefas do
Pi perdidas pelos voluntários e o número total de tarefas.
Para um determinado resultado, é necessário definir a satisfação (ou, usando a termi-
nologia da teoria dos jogos, sua utilidade) de cada jogador. Nesse contexto, dependendo
da natureza do projeto, a satisfação é baseada ou no throughput efetivo de tarefas ou no
tempo médio de terminação de um lote. Ainda, as duas métricas não são expressas na
mesma unidade. Enquanto o throughput deve ser maximizado, o tempo médio de termi-
nação de um lote deve ser minimizado. Por isso, propõe-se traduzir essas métricas numa
única: a métrica de equivalência a cluster ou Cluster Equivalence (CE). Essa métrica
foi utilizada no trabalho de (KONDO et al., 2004) no contexto da otimização do through-
put e representa a quantidade de máquinas dedicadas de referência que seria necessária
para alcançar o mesmo desempenho obtido no sistema analisado. Essa métrica pode ser
calculada para ambos os tipos de projetos, apenas com fórmulas diferentes.
Definição 5 (Equivalência a cluster CE ). Denota-se por W o desempenho (em MFLOP.s−1
)
da máquina de referência escolhida para estimar o CE . Dependendo do objetivo do pro-
jeto i, sua equivalência a cluster pode ser definida como:
CEcontnuo =
TarefasRealizadas · wi
W · TempoTotal
ou como:
CErajada =
bi · wi
W · αi
,
onde αi é o tempo médio de resposta de um lote Pi.
Pode-se, agora, definir a utilidade de cada projeto facilmente:
Definição 6 (Utilidade Ui). A utilidade do Pi é igual a sua equivalência a cluster.
Ui(V, P, S) = CEObji
Obji(Oi(V, P, S))

É importante destacar que a utilidade do Pi depende não somente de sua própria estratégia,
mas também das escolhas das estratégias feitas pelos outros projetos. No restante do texto,
U(V, P, S) denota o vetor de utilidade de todos os projetos.

53
U2
U1
Borda de Pareto
Equilíbrio de Nash
Conjunto de resultados
estritamente superior
ao NE
Figura 4.1: Utilidade para 2 projetos. Qualquer ponto na área cinza corresponde a um
possível resultado (outcome) da interação dos projetos. Diferentes configurações dos pro-
jetos (ou estratégias) podem levar ao mesmo resultado. A borda de Pareto (i.e., o conjunto
de pontos que não são dominados por nenhuma outra estratégia) é destacado com a linha
em negrito. Como o ilustrado, o equilíbrio de Nash pode ser dominado por muitas outras
soluções.
Por consequência, a utilidade de um projeto é aquilo que ele deseja maximizar. Ainda,
como foi observado no contexto do GridBOT (SILBERSTEIN et al., 2009), os projetos
deveriam também tentar garantir que a perda que ele causa aos demais não seja muito
grande. Caso contrário, os voluntários podem considerar esse projeto como egoísta e
decidir não trabalhar mais para ele. Por isso, mesmo que neste trabalho não sejam mode-
ladas tais situações e que os voluntários sejam considerados passivos, não os adicionando,
portanto, nas tomadas de decisões, a perda (não apenas Wi mas W como um todo) deve
ser considerado como um segundo objetivo a ser minimizado.
Na década de 50, John Nash introduziu a noção de Equilíbrio de Nash (ou Nash Equi-
librium) (NASH, 1950, 1951), onde cada jogador otimiza sua própria utilidade e não pode
melhorá-la mudando unilateralmente sua estratégia. Em seguida, formula-se essa noção
com as notações apresentadas anteriormente.
Definição 7 (Equilíbrio de Nash). S é um Equilíbrio de Nash para (V, P) se e somente
se
para todo i e para qualquer S0
i, Ui(V, P, S|Si=S0
i
) 6 Ui(V, P, Si),
onde S|Si=S0
i
denota o conjunto de estratégias onde Pi usa a estratégia S0
i e todos os outros
jogadores mantêm a mesma estratégia como em S.
O equilíbrio de Nash não necessariamente existe e é mesmo irresolúvel determinar sua
existência no caso geral (LUCE; RAIFFA, 1957). Do mesmo modo, ainda que quando
exista, ele pode não ser único e calculá-lo pode ser computacionalmente intratável (NI-
SAN et al., 2007). Além disso, ele é comumente considerado como uma maneira interes-
sante de modelar situações não cooperativas e não coordenadas. Em particular, quando
se considera um sistema onde cada jogador constantemente otimiza sua utilidade e tenta
aprender sua estratégia ótima egoísta, se tal sistema alcança um equilíbrio estável, então
este deve ser um equilíbrio de Nash.
Embora os administradores dos projetos BOINC não necessariamente tentem, conti-
nuamente, refinar os parâmetros dos seus projetos, eles certamente monitoram o resultado

54
de suas políticas. Logo, tal equilíbrio pode ser considerado uma boa aproximação ao que
acontece na vida real.
Os equilíbrios de Nash são, de certa maneira, resultado da otimização não cooperativa
e são estáveis (logo o nome equilíbrio) no sentido que nenhum jogador tem interesse de
unilateralmente alterar sua estratégia. Também, os equilíbrios de Nash não são resisten-
tes a coalizões. Um subconjunto de jogadores poderia ter interesse em simultaneamente
mudar suas estratégias de forma a todos obterem um resultado melhor. Tais noções de
coalizões são conceitos mais avançados de teoria dos jogos (MYERSON, 1997) e não
serão abordados neste texto.
Mais importante, os equilíbrios de Nash não são necessariamente justos nem eficien-
tes. Em particular, eles são geralmente Pareto-ineficientes, isto é, pode existir uma outra
estratégia S0
tal que:
∀Pi : Ui(V, P, S(NE)
) Ui(V, P, S0
).
O seguinte pode ser entendido pelo uso do conjunto de utilidade.
Definição 8 (Conjunto de utilidade (Utility set). O conjunto de utilidade U de um deter-
minado cenário (V, P) é a imagem de todas as estratégias possíveis S pela função U.
A Figura 4.1 mostra o conjunto de utilidade para um cenário imaginário com k = 2
projetos, além da posição do correspondente equilíbrio de Nash. A borda de Pareto é
o conjunto de pontos que não são dominados por nenhuma outra estratégia (i.e., é im-
possível melhorar a utilidade de um jogador sem diminuir a utilidade de outro jogador).
Nota-se que o conjunto de utilidade não, necessariamente, possui uma forma tão simples
quanto àquela usada nesse exemplo ilustrativo.
Não obstante, ser capaz de estimar o quão ruim é um equilíbrio de Nash é muito
importante, uma vez que permite saber quando é válido controlar o sistema ou quando
podemos deixá-lo se auto regular. Noções como o preço da anarquia (ROUGHGARDEN,
2005) ou o fator de degradação do comportamento egoísta (LEGRAND; TOUATI, 2007a)
foram propostas para tratar desse problema. Ainda, calcular os pontos do conjunto de
utilidade ou estimar sua forma é extremamente difícil no caso geral, assim como estimar
sua ineficiência e seus limites. Em vez de calcular exatamente sua forma, os experimentos
descritos no Capítulo 5 visam amostrar as utilidades de forma a fornecer uma idéia de
quão ruim são os equilíbrios na prática.
Finalmente, os equilíbrios de Nash que são Pareto-ineficientes podem levar a situa-
ções dramáticas tais como os paradoxos de Braess (BRAESS, 1968), onde o aumento dos
recursos causa a diminuição da utilidade de cada jogador. Realmente, como o equilíbrio
de Nash não está relacionado diretamente com a borda de Pareto, o aumento dos recursos
causa o melhoramento da borda, mas pode causar um equilíbrio de Nash pior que o an-
terior. Tal fenômeno foi observado inicialmente por Braess (BRAESS, 1968) em 1968 e
ainda é alvo de diversos estudos atualmente. De fato, se a existência de um equilíbrio de
Nash que seja Pareto-ineficiente é uma condição necessária para a ocorrência de um para-
doxo de Braess, ela não é suficiente (para exemplo, veja (LEGRAND; TOUATI, 2007b))
e tal fenômeno não é ainda completamente compreendido. Isto serve, também, como mo-
tivação para o estudo das potenciais ineficiências dos equilíbrios de Nash no contexto dos
sistemas BOINC.

55
5 ESTUDO EXPERIMENTAL
A análise dos complexos algoritmos de escalonamento é extremamente difícil de ser
descrita em equações. Ainda, o resultado da dinâmica de milhares de voluntários rodando
é também complicado de modelar. Portanto, conduziu-se uma série de experimentos para
analisar o desempenho de muitos jogadores independentes compartilhando os recursos
do BOINC. A metodologia da avaliação de desempenho é descrita na Seção 5.1. Como
nosso estudo é multi parâmetro (prazo de término, intervalo de conexão, ...), multi joga-
dor (projetos contínuos e em rajadas) e multi objetivo (tempo de resposta e throughput),
inicialmente é feito um cuidadoso estudo da influência dos parâmetros no desempenho
global do sistema (Seção 5.2). Então, é apresentado o impacto dos projetos em rajadas
nos projetos contínuos (Seção 5.3), Finalmente, explica-se na Seção 5.4, como foram res-
tringidas as possibilidades dos parâmetros, como foi amostrado o conjunto das utilidades
dos projetos e a como foi feita a procura pelos equilíbrios de Nash existentes.
5.1 Definição da configuração
Foi utilizado o simulador proposto na Seção 3.3 para realizar os experimentos. Para
o conjunto de resultados apresentados nesta dissertação, foi usado um conjunto de 1.000
clientes que utilizam traços reais de disponibilidades. Os traços dos clientes foram retira-
dos do projeto SETI@home, disponível através do Failure Trace Archive (FTA) (KONDO
et al., 2010). Foram realizados experimentos com diferentes quantidades de clientes, po-
rém como os resultados foram similares, optou-se por apresentar apenas os resultados
com 1.000 clientes.
Restringiu-se o estudo para as seguintes configurações dos projetos:
• Projetos em rajadas, ou bursts recebem um lote por dia, compostos de apenas ta-
refas de curta duração que duram, em média, 1 hora rodando numa máquina padrão;
• Projetos contínuos têm centenas de milhares de tarefas do tipo CPU-bound. Usa-
se uma configuração típica do projeto SETI@home, com tarefas de 30 horas1
. O
prazo de término dessas tarefas é de 300 horas.
O tempo simulado em cada teste é equivalente a, aproximadamente, 139 dias. É
importante ter um período de tempo longo para garantir a efetividade dos mecanismos
de compartilhamento a longo prazo do sistema BOINC.
1
Veja http://www.boinc-wiki.info/Catalog_of_BOINC_Powered_Projects

56
5.2 Otimização e influência dos parâmetros dos projetos
Esta seção tem como objetivo analisar a influência de cada parâmetro de configuração
no desempenho do projeto em rajada. Na primeira série de experimentos, a carga de
trabalho usada consiste de 4 projetos contínuos (com uma grande quantidade de tarefas)
e 1 projeto em rajada (com 1.000 tarefas por dia). Assume-se que a configuração dos
projetos contínuos não é alterada ao longo do tempo, enquanto no projeto em rajada, são
variados o prazo de término, o intervalo de conexão e a estratégia de escalonamento.
5.2.1 Influência do deadline e do intervalo de conexão
A análise começa com a estratégia de escalonamento mais simples πcste = 1: o ser-
vidor satisfaz todas as requisições enviadas pelos clientes, independentemente da sua po-
tencial capacidade de processar ou não a tarefa no tempo previsto. Assume-se que os
servidores não usam replicação (γcste = 0) para evitar o problema da máquina lenta.
A Figura 5.1 retrata a equivalência a cluster (CE) e a perda de tarefas para os dois
tipos de projetos, quando se varia o slack e o intervalo de conexão do projeto em rajada.
A mais clara observação, vista em todas as figuras, é que o intervalo de conexão tem um
impacto muito limitado, enquanto o prazo de término influencia consideravelmente os
resultados. Em particular, nota-se que a configuração de deadline ótima para o projeto em
rajada é muito pequena (aproximadamente 1 hora) e que uma configuração fora da ideal
causa-lhe uma performance extremamente ruim (veja Figura (5.1.b)).
Um slack muito curto (menor que 1) cria uma perda excessivamente grande para o pro-
jeto em rajada (Figura (5.1.d)) e pode até mesmo dobrar o desperdício dos projetos contí-
nuos (Figura (5.1.c)). Apesar disso, ele continua sendo baixo se comparado ao do projeto
em rajada. Ainda, o prazo de término curto pode levar a um CE baixo para ambos proje-
tos em rajadas (Figura (5.1.b)) e contínuos (Figura (5.1.a)). Por outro lado, os prazos de
término mais longos não afetam consideravelmente os projetos contínuos (Figura (5.1.a)),
mas causam um desempenho ruim para os projetos em rajadas (Figura (5.1.b)).
Uma amostragem mais fina dos valores dos parâmetros próximos aos valores interes-
santes foi realizada e é apresentada na Figura 5.2. Ela permite verificar que uma confi-
guração do slack σcste = 1.1 e um intervalo de conexão (τcste = 2) possuem o melhor
CE para o projeto em rajada (CErajada = 125) (Figura (5.2.b)). É interessante destacar
que essa configuração não degrada significantemente o CE dos projetos contínuos (Fi-
gura (5.2.a)), o que é um bom sinal para a coexistência de ambos projetos. Por fim, em-
bora o desperdício de tarefas para os projetos contínuos continue baixa quando o projeto
em rajada seleciona seu conjunto de parâmetros de configuração ótimo (2.5% comparado
com um mínimo absoluto de 1.8% como pode ser visto na Figura (5.1.c)), a perda dele é
extremamente alta (aproximadamente 56% na Figura (5.2.d)).
5.2.2 Influência das estratégias de escalonamento
5.2.2.1 Saturação
Esta seção analisa a estratégia de escalonamento πsat, onde o teste de saturação, con-
forme descrito na Seção 2.2.2, é aplicado antes do envio das tarefas. Nenhuma estratégia
de replicação é utilizada para podermosr comparar com os resultados da Seção 5.2.1.
De modo geral, as formas das curvas são bem similares como podemos ver na Fi-
gura 5.3. O melhor desempenho para o projeto em rajada é com os parâmetros de
1.1 horas de prazo de término e 2 horas de intervalo de conexão, atingindo nesse caso
CErajada = 122, o qual é um pouco menor que para a estratégia fixa. No caso dos proje-

57
Projetos contínuos Projeto em rajada
CE
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
40
110
112
114
116
118
120
122
124
126
CE
Deadline (h)
Intervalo de Conexão (h)
CE
110
112
114
116
118
120
122
124
126
(1.a)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
40
20
30
40
50
60
70
80
90
100
110
120
130
CE
Deadline (h)
CE
20
30
40
50
60
70
80
90
100
110
120
130
(1.b)
Perda
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
40
0.018
0.02
0.022
0.024
0.026
0.028
0.03
0.032
Deadline (h)
0.018
0.02
0.022
0.024
0.026
0.028
0.03
0.032
Waste
(1.c)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
40
0
10
20
30
40
50
60
Deadline (h)
0
10
20
30
40
50
60
Waste
Waste
(1.d)
Figura 5.1: Análise da influência do prazo de término e do intervalo de conexão no CE e
na perda usando a estratégia fixa de escalonamento.
CE
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
110
112
114
116
118
120
122
124
CE
Deadline (h)
CE
110
112
114
116
118
120
122
124
(2.a)
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
60
70
80
90
100
110
120
130
CE
Deadline (h)
CE
60
70
80
90
100
110
120
130
(2.b)
Perda
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0.021
0.022
0.023
0.024
0.025
0.026
0.027
0.028
0.029
0.03
0.031
Deadline (h)
0.021
0.022
0.023
0.024
0.025
0.026
0.027
0.028
0.029
0.03
0.031
Waste
Waste
(2.c)
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.5
1
1.5
2
Deadline (h)
0.4
0.6
0.8
1
1.2
1.4
1.6
Waste
Waste
(2.d)
na perda usando a estratégia fixa de escalonamento.

58
CE
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
122
124
126
128
130
132
134
136
138
CE
Deadline (h)
CE
122
124
126
128
130
132
134
136
138
(3.a)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(3.b)
Perda
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0.016
0.017
0.018
0.019
0.02
0.021
0.022
Deadline (h)
0.016
0.017
0.018
0.019
0.02
0.021
0.022
Waste
Waste
(3.c)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Deadline (h)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Waste
Waste
(3.d)
na perda usando a estratégia saturação de escalonamento.
CE
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
120
122
124
126
128
130
132
134
136
138
CE
Deadline (h)
CE
120
122
124
126
128
130
132
134
136
138
(4.a)
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(4.b)
Perda
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
Deadline (h)
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
Waste
Waste
(4.c)
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.2
0.4
0.6
0.8
1
Deadline (h)
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
Waste
Waste
(4.d)
na perda usando a estratégia saturação de escalonamento.

59
tos contínuos, é importante ressaltar o aumento do CE à medida que o prazo de término
do projeto em rajada se aproxima de 0 (Figura 5.4.a). Pois, com um prazo muito curto,
dificilmente a máquina é capaz de terminar a tarefa a tempo e logo, o teste de saturação
evita o seu envio. Dessa forma, os projetos contínuos recuperam esses recursos ociosos
do projeto em rajada e este tem seu desempenho drasticamente afetado (Figura 5.4.b).
No que diz respeito ao desperdício, temos uma forma mais homogênea, sem o au-
mento excessivo como no caso da estratégia fixa (Figura 5.4.b). A exceção é quando
tanto o deadline quanto o intervalo de conexão são curtos, quando o número de tarefas
enviadas é maior e consequentemente, a perda também. Analisando a configuração ótima
para o projeto em rajada, a perda é de, aproximadamente, 12% ao invés de 56% como na
estratégia anterior (Figura 5.4.d). Os projetos contínuos, por sua vez, são pouco afetados
pelo projeto em rajada já que seu desperdício varia apenas 0.007 (Figura 5.4.c).
5.2.2.2 EDF
Esta seção analisa os resultados obtidos com a estratégia de escalonamento πEDF e as
mesmas configurações das seções anteriores. Como podemos ver nas Figuras 5.3 e 5.5,
a superfície que ilustra o desempenho das estratégias de saturação e EDF são similares.
Ambas as estratégias retornam para cada projeto aproximadamente o mesmo CE e uma
perda baixa (exceto para os projetos em rajadas que é perto de 12%). A grande diferença
entre as estratégias ocorre no desperdício com os parâmetros (deadline e intervalo de
conexão) próximos ao 0. Como o teste de EDF verifica todas as tarefas rodando no cliente,
ele evita o envio de muitas tarefas e o consequente descarte das mesmas. Ainda, é possível
que a estratégia πEDF obtenha um resultado superior a πsat em situações mais complexas.
Esse comportamento é o resultado da combinação das duas estratégias na política
local de escalonamento do cliente: EDF e a equidade a longo prazo. O projeto em rajada
consegue acessar os recursos quando necessário, rodando suas tarefas com uma prioridade
maior e obtendo seus resultados rapidamente. Por outro lado, a equidade a longo prazo
garante que os projetos contínuos obtenham ao menos uma fatia razoável dos recursos,
evitando que sejam postergados indefinidamente.
5.2.3 Réplicas
A seção anterior apresentou os parâmetros de prazo de término e intervalo de conexão
que os projetos em rajadas devem escolher para otimizar seu desempenho. Esta seção
descreve, brevemente, a influência do uso da replicação no desempenho dos projetos em
rajadas. Para realizar esse estudo, escolheu-se a melhor configuração usando a estratégia
fixa de escalonamento e variou-se o número de réplicas extras de cada tarefa que o projeto
em rajada utiliza.
Como podemos ver na Figura 5.7, o projeto em rajada pode melhorar seu desempenho
em aproximadamente 7% usando 2 réplicas (γcste = 2). Além disso, o uso de um número
maior de réplicas causa um decréscimo no CE, devido ao número maior de tarefas dispu-
tando os mesmos recursos. Surpreendentemente, o uso de replicação também diminui o
desperdício de 56.5% para 48%, apesar de que no geral ela se manteve alta.
Após a verificação do número de cópias ótimo para o melhor desempenho do projeto
em rajada, é necessário determinar, novamente, quais os melhores parâmetros de inter-
valo de conexão e prazo de término quando se usam as réplicas. Os gráficos referentes
a esse estudo são apresentados no Apêndice A. A Figura 5.8 resume os resultados obti-
dos nos diferentes estudos e podemos ver que de maneira geral os resultados não foram
influenciados consideravelmente pelo uso da replicação.

60
CE
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
122
124
126
128
130
132
134
136
138
CE
Deadline (h)
CE
122
124
126
128
130
132
134
136
138
(5.a)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(5.b)
Perda
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0.016
0.017
0.018
0.019
0.02
0.021
0.022
Deadline (h)
0.016
0.017
0.018
0.019
0.02
0.021
0.022
Waste
Waste
(5.c)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
Deadline (h)
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
Waste
Waste
(5.d)
na perda usando a estratégia EDF de escalonamento.
CE
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
122
124
126
128
130
132
134
136
138
CE
Deadline (h)
CE
122
124
126
128
130
132
134
136
138
(6.a)
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(6.b)
Perda
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
Deadline (h)
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
Waste
Waste
(6.c)
0.5
1
1.5
2
2.5
3 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
Deadline (h)
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
0.45
0.5
0.55
Waste
Waste
(6.d)
na perda usando a estratégia EDF de escalonamento.

61
0.48
0.50
0.52
0.54
0.56
0.58
0 2 4 6 8 10
Waste
126
128
130
132
134
136
138
CE
Número de Réplicas
Figura 5.7: Influência da replicação no CE e perda usando uma estratégia fixa de escalo-
namento para o projeto em rajadas.
Fixed
Saturation
EDF
Fixed rep
Saturation rep
EDF rep
0
50
100
150
200
250
0 50 100 150 200 250
CE
−
Continuous
CE − Burst
Fixed
Saturation
EDF
Fixed rep
Saturation rep
EDF rep
0
0.1
0.2
0.3
0.4
0.5
0.6
0 0.1 0.2 0.3 0.4 0.5 0.6
Waste
−
Continuous
Waste − Burst
Figura 5.8: Comparando o CE e a perda das estratégias de escalonamento.

62
Projetos Contínuos
Projetos Bursts
0.0
20.0
40.0
60.0
80.0
100.0
120.0
140.0
0 500 1000 1500 2000 2500
CE
Tamanho do Burst
Figura 5.9: Análise da influência do tamanho dos lotes do projeto em rajada no CE usando
a estratégia de saturação no escalonamento.
Por fim, é interessante notar que a estratégia fixa possui um CE levemente superior
devido ao grande número de tarefas enviadas, que por sua vez, incorre em uma perda de
tarefas importante (próximo de 48% na configuração ótima). Na maior parte dos experi-
mentos, observou-se que a estratégia fixa frequentemente inunda o sistema com tarefas.
Embora seja a maneira mais eficiente para os projetos em rajadas roubarem os recursos
computacionais disponíveis dos projetos contínuos, ela causa o aumento excessivo das
tarefas perdidas. Nessas condições, os servidores deveriam abandonar essa política de es-
calonamento já que ela desperdiça recursos e pode causar o descontentamento dos clientes
(causado pela perda dos créditos das tarefas perdidas). Salienta-se que a perda importante
de tarefas de tal estratégia já foi identificada por Kondo et al. (KONDO; ANDERSON;
MCLEOD, 2007). Entretanto, ela foi apenas comparada com a estratégia EDF e conside-
rada como custosa e, portanto, frequentemente desativada. Problemas similares sobre a
insatisfação dos usuários foram também relatados em (SILBERSTEIN et al., 2009).
5.3 Influência dos projetos em rajadas nos projetos contínuos
5.3.1 Influência do tamanho da rajada
Apesar da grande quantidade de tarefas perdidas para o projeto em rajada, a con-
figuração analisada nas seções anteriores parecia indicar que os dois tipos de projetos,
contínuos e em rajadas, poderiam compartilhar os recursos sem problemas. Ainda, esse
bom comportamento é majoritariamente devido ao fato que os projetos em rajadas não
esgotam os recursos disponíveis. Esta seção apresenta a influência do tamanho dos lo-
tes dos projetos em rajadas no desempenho do sistema, de maneira a visualizar o que
ocorre quando os recursos se tornam escassos. A carga de trabalho é a mesma da seção
anterior: 4 projetos contínuos e 1 projeto em rajada, todos usando a política de escalo-
namento saturação (πsat). O projeto em rajada utiliza um slack σcste = 1.1 e o intervalo
de conexão τcste = 2 (os parâmetros de configuração ótimos conforme determinado pelos
experimentos realizados).
Como é possível ver na Figura 5.9, o CE do projeto em rajada alcança o máximo
quando o projeto em rajada tem aproximadamente 1.000 tarefas por dia. Após isso, o
sistema começa a ficar saturado e, consequentemente, o CE diminui. Contudo, o projeto
em rajada não rouba mais recursos do projeto contínuo quando ele possui muitas tarefas.
Isso é devido à equidade do sistema que garante o CE dos projetos contínuos. Analisando
a perda, retratado na Figura 5.10 (note a escala logarítmica no eixo Y), podemos ver uma
importante influência no desperdício dos projetos contínuos, já que ela quase duplica com

63
Projetos Contínuos
Projetos Bursts
0.016
0.031
0.062
0.125
0.250
0.500
0 500 1000 1500 2000 2500
Waste
Tamanho do Burst
Figura 5.10: Análise da influência do tamanho dos lotes do projeto em rajada na perda
usando a estratégia de saturação no escalonamento (note a escala logarítmica no eixo Y).
o aumento do tamanho das rajadas dos projetos. Outro fato interessante que podemos ver
nesta figura é a estabilização na perda das tarefas após um limiar. Deve-se isto ao teste
de saturação, o qual evita o envio de tarefas aos clientes e o esgotamento completo do
sistema.
5.3.2 Influência do número de projetos em rajadas
O número de projetos em rajadas no sistema pode também afetar a quantidade de
tarefas perdidas pelos projetos contínuos. Nesta seção, fixamos o número total de projetos
que os clientes trabalham em 8 e variamos o número de projetos em rajadas. Cada projeto
recebe um lote de 1.000 tarefas por dia cujo prazo de término é de 1.1 horas.
Projetos Contínuos
Projetos Bursts
0
50
100
150
200
250
300
350
0 1 2 3 4 5 6 7 8
CE
Médio
Número de Projetos Bursts
Figura 5.11: Analisando o impacto dos projetos em rajadas no CE usando a estratégia de
escalonamento de saturação.
Considerando o CE, a Figura 5.11 mostra que o CE dos projetos contínuos aumenta
conforme o número de projetos em rajadas aumenta, uma vez que eles não utilizam todos
os recursos a que teriam direito (ao contrário dos projetos contínuos). Mesmo com o uso
da estratégia saturação para o escalonamento (πsat), pode-se observar que na Figura 5.12,
a perda do projeto contínuo aumenta de aproximadamente 3% com 1 projeto em rajada
para 7% com 7 projetos em rajadas.
Nota-se que o trabalho (KONDO; ANDERSON; MCLEOD, 2007) já afirmava que
uma política fixa no envio de tarefas poderia causar taxas de perdas de tarefas inacei-
tavelmente altas. Entretanto, até onde sabemos, não era conhecido que essa estratégia
poderia causar o aumento do desperdício para outros projetos. Esse fenômeno é ilustrado
na Figura 5.13, a qual representa a perda de tarefas quando se troca projetos contínuos por
projetos em rajadas, usando a estratégia de escalonamento fixa e uma carga de trabalho de

64
Projetos Contínuos
Projetos Bursts
0.01
0.02
0.03
0.04
0.05
0.06
0.07
0.08
0.09
0.1
0 1 2 3 4 5 6 7 8
Waste
Médio
Figura 5.12: Analisando o impacto dos projetos em rajadas na perda usando a estratégia
de escalonamento de saturação.
Projetos Bursts
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0 1 2 3 4 5 6 7 8
Waste
Médio
Projetos Contínuos
Figura 5.13: Analisando o impacto dos projetos em rajadas na perda usando a estratégia
de escalonamento fixa.
1 lote com 1.700 tarefas por dia. Apesar do desperdício dos projetos em rajadas permane-
cer estável a medida que o número de projetos aumenta, a perda dos contínuos aumenta
consideravelmente (de apenas 3% para mais de 50%). Assim, temos que o protocolo atual
do BOINC não é capaz de garantir a equidade e a isolação dos projetos quando existem
projetos em rajadas no ambiente.
Examinando os resultados dos nossos testes, conclui-se que os projetos em rajadas
têm uma influência importante na quantidade de tarefas perdidas dos outros projetos e
portanto, eles podem causar a insatisfação do cliente que doa seus recursos, pois estes
perderão mais tarefas e créditos.
5.4 Equilíbrio de Nash e amostras do conjunto de utilidade
Nesta seção é explicado como foi realizada a busca pelos equilíbrios de Nash, além
de localizá-los numa amostra do correspondente conjunto de utilidade.
5.4.1 Estratégia da melhor resposta
Na Seção 5.2, mostrou-se que o prazo de término é o parâmetro mais influente no
desempenho dos projetos em rajadas e que as outras configurações têm um valor ótimo
praticamente independente do prazo de término. Portanto, considera-se uma situação
onde todos os projetos utilizam a estratégia de saturação com uma replicação fixa de 2 e
um intervalo de conexão de 2 horas.

65
50
55
60
65
70
75
80
1 1.11.21.31.41.51.61.71.81.9 2 2.12.22.32.42.52.62.72.82.9 3 3.13.23.33.43.5
CE
Deadline (h)
Consenso
Burst Dissidente
Bursts Não−Dissidentes
Equilíbrio de Nash
Figura 5.14: Ilustrando o incentivo de um projeto alterar seu deadline a partir de um es-
tado de consenso. A linha de consenso representa o CE CEcons de cada projeto em rajada
se eles concordam com um certo deadline σcons. A linha divergente representa quando
um projeto dissidente pode melhorar seu CEdis selecionando um deadline diferente σdis.
O impacto de tal modificação da estratégia no CE dos demais projetos é representada pela
linha CEnao−dis.
Primeiramente é apresentada uma configuração do ambiente com 6 projetos, dos quais
4 deles são projetos em rajadas, recebendo 1 lote de 900 tarefas de 1 hora por dia. Nessa
configuração, os projetos contínuos possuem tarefas de 24 e 30 horas com um prazo de tér-
mino de 336 e 300 horas (esses valores são representativos dos projetos Einstein@home
e SETI@home, respectivamente).
Embora uma estratégia de melhor resposta não, necessariamente, convirja, é sabido
que no caso de haver uma convergência, o estado limite é um equilíbrio de Nash. Além
disso, como na configuração particular analisada, todos os projetos em rajadas são idên-
ticos, eles devem todos ter a mesma configuração no equilíbrio. Portanto, foi aplicada a
seguinte metodologia (assumindo que os projetos em rajadas consentem com um deter-
minado valor de slack σcons):
1. Calcula-se o CEcons dos projetos em rajadas (valor de consenso na Figura 5.14).
2. Para um determinado valor de slack σcons, um projeto em rajada dissidente pode
aumentar seu CE, unilateralmente, alterando seu slack para um valor diferente σdis.
Calcula-se o novo valor do slack σdis do projeto em rajada dissidente.
3. Ainda, essa modificação de estratégia normalmente resulta num decréscimo do
CEnao−dis dos outros projetos em rajadas.
Calcula-se o novo valor de CEnao−dis resultante da divergência de um dos projetos
em rajadas. Ambos CEdis e CEnao−dis são representados na Figura 5.14.
Por exemplo, quando o σcons = 1.15 (i.e., um valor próximo daquele ótimo encontrado
nas seções anteriores), podemos ver que o projeto em rajada pode melhorar seu CE de
71.3 para 77.5, apenas mudando seu slack. Esse comportamento (mudança de CE do
projeto em rajada) causa uma diminuição do CE dos demais projetos em 2 unidades.

66
1
1.5
2
2.5
3
3.5
1 1.5 2 2.5 3 3.5
Deadline − Base
Deadline
−
Tendência
da melhor resposta
Trajetória
convergente
da melhor resposta
Trajetória
cíclica
Equilíbrio de Nash
Pontos de começo arbitrários
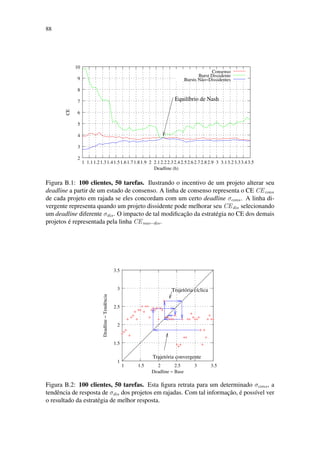
Figura 5.15: Esta figura retrata para um determinado σcons, a tendência de resposta de σdis
dos projetos em rajadas. Com tal informação, é possível ver o resultado da estratégia de
melhor resposta.
Consequentemente, os outros projetos tendem a abandonar seu σcons = 1.15 e mudar
para uma melhor posição também. Interessantemente, as 3 curvas se encontram no ponto
σi = 2.45, o qual é, portanto, o equilíbrio de Nash desse ambiente.
A Figura 5.15 retrata para um dado σcons, o correspondente σdis que leva para um me-
lhor CEdis. Logo, se todos os projetos usam uma estratégia simples de melhor resposta,
podemos seguir a dinâmica do sistema e verificar para onde ele converge. No caso da
posição inicial ser σinit ∈ [1.8, 2.45], vemos que ele converge para o equilíbrio de Nash
σNE = 2.45, o qual causa um CENE = 60.7 para todos os projetos em rajadas. Ainda,
podemos ler na Figura 5.16 que uma escolha comum de σcons = 1.15 (veja o ponto de
referência indicado na figura) levaria a um CEcons = 71.3 CENE.
Ainda, poderia acontecer que essa perda de eficiência para os projetos em rajadas
beneficiasse os projetos contínuos. Infelizmente, não é o que acontece já que podemos,
facilmente, verificar que os resultados dos projetos contínuos são piores. Para isto, basta
analisar o outcome de tais situações no espaço de utilidade ilustrado na Figura 5.16.
Com tal representação, podemos confirmar que o equilíbrio de Nash é Pareto-ineficiente
e que o CE pode ser melhorado em mais de 10% para os projetos se todos, colaborativa-
mente, escolhessem σcons = 1.15.
Tais ineficiências, como as vistas anteriormente, podem ser observadas em diversas
configurações e o conjunto de utilidade sempre possui, mais ou menos, a mesma estru-
tura. Por exemplo, quando usamos uma configuração um pouco diferente, composta de
8 projetos, dos quais 7 são projetos em rajadas recebendo lotes de 600 tarefas de 1 hora
por dia, obtém-se um equilíbrio de Nash ineficiente (veja a Figura 5.19). Note que nesse
exemplo, o projeto contínuo possui tarefas de 30 horas com prazo de término de 300
horas, como já dito, é uma configuração típica do projeto SETI@home. Mais algumas
configurações, variando-se o número de clientes utilizados são apresentadas no Apêndice
B.
Analisando a Figura 5.17, vemos que os projetos em rajadas têm um grande incentivo
de modificar seu slack quando o CE atinge o ponto de maior valor (1.25) (veja o CEdis
na figura). Ainda, analisando a Figura 5.18 que retrata a convergência das estratégias

67
NE
Ponto de Referência
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
1.4
1.45
1.5
1.55
1.6
1.65
1.7
1.75
1.8
1.85
1.9
1.95
2
2.05
2.1
2.15
2.2
2.25
2.3
2.35
2.4
2.45
2.5
2.55
2.6
2.65
2.7
2.75
2.8
2.85
2.9
2.95
3
3.05
3.1
3.15
3.2
3.25
3.3
3.35
3.4
3.45
3.5
165
170
175
180
185
190
195
56 58 60 62 64 66 68 70 72 74
CE − Burst
Burst − Deadline(h)
CE
−
Contínuos
Figura 5.16: Amostrando o conjunto de utilidade e ilustrando a ineficiência do equilíbrio
de Nash. 2 projetos contínuos e 4 projetos em rajadas com 900 tarefas de 1 hora por
dia. CE pode ser melhorado em mais de 10% para todos os projetos caso seja escolhido,
colaborativamente, σcons = 1.15 ao invés do NE (σNE = 2.45).
Equilíbrio de Nash
Consenso
Burst Dissidente
20
30
40
50
60
70
80
90
100
110
1 1.11.21.31.41.51.61.71.81.9 2 2.12.22.32.42.52.62.72.82.9 3 3.13.23.33.43.5
CE
Deadline (h)
Figura 5.17: Ilustrando o incentivo de um projeto alterar seu deadline a partir de um es-
tado de consenso. A linha de consenso representa o CE CEcons de cada projeto em rajada
se eles concordam com um certo deadline σcons. A linha divergente representa quando
um projeto dissidente pode melhorar seu CEdis selecionando um deadline diferente σdis.
O impacto de tal modificação da estratégia no CE dos demais projetos é representada pela
linha CEnao−dis.

68
NE
Trajetória convergente
1
1.5
2
2.5
3
3.5
1 1.5 2 2.5 3 3.5
Deadline − Base
Deadline
−
Tendência
Figura 5.18: Esta figura retrata para um determinado σcons, a tendência de resposta de σdis
dos projetos em rajadas. Com tal informação, é possível ver o resultado da estratégia de
melhor resposta.
NE
Ponto de Referência
1.05
1.1
1.3
1.35
1.4
1.45
1.5
1.55
1.6
1.65
1.7
1.75
1.8
1.85
1.9
1.95
2
2.05
2.1
2.15
2.2
2.25
2.3
2.35
2.4
2.45
2.5
2.55
2.6
2.65
2.7
2.75
2.8
2.85
2.9
2.95
3
3.05
3.1
3.15
3.2
3.25
3.3
3.35
3.4
3.45
3.5
305
310
315
320
325
330
335
340
345
350
355
34 35 36 37 38 39 40 41
CE − Burst
1
1.15
1.2
1.25
CE
−
Contínuos
Figura 5.19: Amostrando o conjunto de utilidade e ilustrando a ineficiência do equilíbrio
de Nash. 1 projeto contínuo e 7 projetos em rajadas com 600 tarefas de 1 hora por dia.
CE pode ser melhorado mais de 10% para os projetos em rajadas e de 7% para os projetos
contínuos escolhendo, colaborativamente, σcons = 1.25 ao invés do NE (σNE = 2.45).

69
adotadas, temos que as estratégias dos jogadores tendem rapidamente para o NE.
Novamente, pode-se verificar na representação que o equilíbrio de Nash é de fato
Pareto-ineficiente. Ainda, o CE poderia ser melhorado em mais de 10% para os projetos
em rajadas e de 7% para o projeto contínuo caso fosse escolhido um σcons = 1.25 para os
em rajadas (veja o ponto de referência na Figura 5.19).
Este capítulo realizou uma análise de desempenho de um ambiente onde projetos em
rajadas e projetos contínuos disputam os recursos de um grupo de clientes. Primeira-
mente, buscou-se descobrir os melhores parâmetros de replicação, prazo de término, in-
tervalo de conexão e estratégia de escalonamento para os projetos em rajadas. Esse estudo
mostrou que os projetos em rajadas tendem a utilizar um prazo de término extremamente
curto de forma a obter as tarefas mais rapidamente. Além disso, vimos que o intervalo de
conexão e a estratégia de escalonamento pouco influenciaram nos resultados obtidos.
Em seguida, verificou-se o impacto do número de projetos em rajadas e do número
de tarefas no desperdício e no CE dos projetos. Viu-se que os projetos em rajadas podem
ocasionar variações negativas em ambos critérios nos demais projetos. Diante disso, foi
feito o estudo do Equilíbrio de Nash da interação dos projetos. Os experimentos condu-
zidos permitiram concluir que muitas vezes os projetos em rajadas tendem a convergir
para um NE. Ainda, vimos que esse NE é ineficiente e que os projetos poderiam ter um
desempenho melhor caso concordassem em utilizar um conjunto de parâmetros comum.
A principal conclusão dos experimentos é que os projetos em rajadas não apenas pre-
judicam o desempenho entre si, mas também, possuem um impacto negativo para a efici-
ência dos projetos contínuos. Logo, é necessário ter precaução no momento de configurar
os servidores dos projetos BOINC, evitando assim, possíveis perdas recorrentes da para-
metrização ruim dos mesmos.

71
6 CONCLUSÃO E TRABALHOS FUTUROS
Os sistemas de Computação Voluntária surgiram como uma alternativa de baixo custo
para a resolução de problemas científicos que necessitam de grande quantidade de pro-
cessamento. Graças à popularização dos computadores e da Internet, é possível agregar
grande parte desse poder computacional disponível distribuído em máquinas ao redor do
mundo. Entre tais plataformas, o BOINC foi a que se tornou mais famosa, sendo utilizada
por diversos projetos. Tal plataforma vem sendo usada com sucesso no contexto de pro-
jetos com grande quantidade de tarefas independentes e cujo interesse seja o número total
de tarefas realizadas. Entretanto, desafios emergem do seu uso com cargas de trabalho
com características diferentes.
Para atingir alta escalabilidade e robustez, a infra-estrutura do BOINC é baseada em
mecanismos de escalonamento descentralizados. Os clientes se registram nos projetos
para os quais desejam trabalhar e implementam um misto de equidade de curto e longo
prazo para selecionar as tarefas a rodar em sua máquina. Do lado do projeto, cada um
possui seu próprio servidor e muitos parâmetros de configuração podem ser seleciona-
dos para se adaptar às características das suas tarefas, e consequentemente, influenciar
seu desempenho. Dessa forma, é extremamente difícil de analisar o sistema através de
equações, e portanto, as pesquisas nessa área são baseadas em experimentação.
Diversos simuladores foram criados especificamente para o estudo na área de CV.
Para atingir bons níveis de escalabilidade, grande parte dos simuladores existentes usam
opções mais simples no seu design, com o custo da perda de realismo e extensibilidade.
Logo, a primeira contribuição desta dissertação são as melhorias propostas para o si-
mulador de propósito geral SimGrid. Ao longo do texto, foi apresentado e analisado o
funcionamento interno do SimGrid, o qual tem um bom realismo e extensibilidade, mas
possuía gargalos de desempenho e escalabilidade quando utilizado para simulações em
CV. Então, foram propostas e implementadas as melhorias que permitiram remover esse
gargalo. As modificações foram avaliadas e mostraram que a nova versão do SimGrid é
consideravelmente mais rápida que a anterior.
Ainda, implementou-se um simulador para a arquitetura BOINC, o qual possui as
principais funcionalidades do sistema. Em seguida, foram realizados testes para compará-
lo com alguns dos simuladores específicos do BOINC existentes. Demonstrou-se, então,
a sua capacidade de conduzir experimentos complexos com a interação de diversos servi-
dores e clientes do BOINC.
Através do simulador criado, foram estudadas situações onde os projetos tradicionais,
interessados no throughput de tarefas interagem com projetos em rajadas que estão in-
teressados no tempo médio de resposta das tarefas. Ainda, estes possuem uma carga de
trabalho diferente, composta de lotes de tarefas que chegam ao sistema de forma não
constante. Efetuou-se uma modelagem baseada em teoria dos jogos e uma análise ex-

72
perimental do sistema, no intuito de verificar os potenciais problemas de desempenho
existentes em tais configurações complexas. É importante ressaltar que tais conceitos da
teoria dos jogos são raramente aplicados em sistemas complexos, tais como o BOINC. De
fato, o modelo proposto considera um espaço de estratégia muito grande, um número de
jogadores suficientemente grande e um problema de otimização multi objetivo, já que os
projetos não apenas devem otimizar seu throughput ou seu tempo de resposta dos lotes,
mas também, diminuir a sua quantidade de tarefas perdidas (i.e., quantidade de tarefas
que perderam seu prazo de término) e a perda causada aos outros projetos.
O estudo experimental realizado permite a análise da influência dos principais parâ-
metros do servidor (replicação, prazo de término das tarefas, políticas no envio de tarefas,
entre outros) no contexto dos diversos jogadores. Ainda, este estudo demonstra que o
mecanismo atual de escalonamento do BOINC é incapaz de garantir a justiça, equidade
e a isolação entre os projetos (os projetos em rajadas podem prejudicar drasticamente o
desempenho dos outros projetos).
Em particular, mostrou-se que quando tais projetos em rajadas compartilham as má-
quinas dos voluntários com projetos contínuos, a otimização não cooperativa das confi-
gurações dos projetos pode resultar em ineficiências no compartilhamento dos recursos.
Apresentou-se diversas situações onde cada projeto poderia utilizar os recursos com maior
eficiência (mais de 10%), caso os projetos em rajadas concordassem em alguns dos pa-
râmetros de escalonamento escolhidos. Embora esses resultados possam não surpreender
pesquisadores da área de teoria dos jogos, até o nosso conhecimento, esta é a primeira
vez que tais equilíbrios de Nash ineficazes são apresentados no contexto dos sistemas de
Computação Voluntária. É interessante notar que essas ineficiências ocorrem mesmo que
todo o sistema se baseie num protocolo no qual cada voluntário produza, localmente, um
compartilhamento justo e eficiente dos seus recursos computacionais disponíveis.
Como trabalhos futuros, inicialmente temos o aperfeiçoamento do simulador utili-
zado, considerando alguns fatores que não foram cobertos nesse estudo inicial. No lado do
cliente, as principais alterações seriam o uso de checkpoint, a implementação dos meca-
nismos de crédito e as restrições das configurações das máquinas (memória RAM, disco,
sistema operacional, entre outros). No comportamento do servidor, as principais modifi-
cações seriam uma possível implementação da cache de tarefas disponíveis para o envio
ao clientes e a verificação dos requisitos mínimos de configuração de máquina necessários
para as tarefas. Essas alterações permitiriam um simulador com um comportamento mais
próximo ao ambiente real do BOINC.
Nas políticas de escalonamento dos servidores dos projetos do BOINC melhorias po-
dem ser feitas no sentido de refinar os métodos de escalonamento, principalmente o de
saturação e o EDF. Ainda, algoritmos que levem em conta o histórico de disponibili-
dade do cliente poderiam ser implementados no servidor do BOINC atual, diminuindo
portanto, o número de tarefas perdidas pelos clientes.
No âmbito da pesquisa da interação dos projetos em rajadas e dos projetos contínuos,
temos a continuação da análise das situações onde os equilíbrios de Nash ocorrem. A
variação do número de projetos, número de tarefas e características dos projetos (tipos e
tamanho das tarefas, prazo de término, número de réplicas, etc) permitiria a caracteriza-
ção das cargas de trabalho onde o problema é evidente, e consequentemente, auxiliaria
a decisão de deixar o sistema se auto-regular ou da necessidade de implementar algum
mecanismo de prevenção na arquitetura do BOINC para que esse problema não ocorra.
É importante ressaltar que a existência dos equilíbrios de Nash pode levar o sistema
a comportamentos ainda mais indesejáveis, como por exemplo os paradoxos de Braess.

73
Nesse tipo de paradoxo, o aumento dos recursos da plataforma, ou seja a inclusão de
novos clientes, pode degradar ao invés de melhorar o desempenho do sistema como um
todo. Nota-se que a teoria dos jogos fornece algumas ferramentas (mecanismos de preços,
valores de Shapley, etc) para tratar e melhorar tais situações e algumas delas poderiam ser
usadas para implementar uma forma de cooperação entre os projetos. Entretanto, para
realizar a escolha correta da melhor ferramenta disponível é necessário o completo enten-
dimento do comportamento da plataforma. Logo, é evidente a importância da realização,
e por consequência, continuação de um estudo como o da análise da interação entre os
projetos realizada nesta dissertação.

75
REFERÊNCIAS
ANDERSON, D. P. BOINC: a system for public-resource computing and storage. In:
IEEE/ACM INTL. WORKSHOP ON GRID COMPUTING, 5., 2004. Proceedings...
[S.l.: s.n.], 2004.
ANDERSON, D. P.; COBB, J.; KORPELA, E.; LEBOFSKY, M.; WERTHIMER, D.
SETI@home: an experiment in public-resource computing. Commun. ACM, New York,
NY, USA, v.45, n.11, 2002.
ANDERSON, D. P.; MCLEOD VII, J. Local Scheduling for Volunteer Computing. In:
INTL. PARALLEL AND DISTRIBUTED PROCESSING SYMP. (IPDPS 2007), 2007.
Proceedings... IEEE Intl., 2007.
ANDERSON, D. P.; REED, K. Celebrating Diversity in Volunteer Computing. In: SYS-
TEM SCIENCES, 2009. HICSS ’09. 42ND HAWAII, 2009. Anais... [S.l.: s.n.], 2009.
BARISITS, M.; BOYD, W. MartinWilSim Grid Simulator. 2009. Summer Internship
— Vienna UT and Georgia Tech, CERN, Switzerland. Disponível em: http://www.
slideshare.net/wbinventor/slides-1884876. Acesso em: 10 ago. 2010.
BERTSEKAS, D.; GALLAGER, R. Data Networks. [S.l.]: Prentice-Hall, 1992.
BRAESS, D. Über ein Paradoxen aus der Verkehrsplanung. Unternehmensforschung,
[S.l.], v.12, p.258–268, 1968.
BUYYA, R.; MURSHED, M. GridSim: a toolkit for the modeling and simulation of
distributed resource management and scheduling for grid computing. Concurrency and
Computation: Practice and Experience, [S.l.], v.14, n.13-15, 2002.
CAPPELLO, F.; DJILALI, S.; FEDAK, G.; HERAULT, T.; MAGNIETTE, F.; NERI, V.;
LODYGENSKY, O. Computing on Large Scale Distributed Systems: xtremweb architec-
ture, programming models, security, tests and convergence with grid. Future Generation
Computer Systems, [S.l.], v.21, n.3, 2004.
CAPPELLO, F.; FEDAK, G.; KONDO, D.; MALéCOT, P.; REZMERITA, A. Handbook
of Research on Scalable Computing Technologies. [S.l.]: IGI Global, 2009.
CASANOVA, H. Simgrid: a toolkit for the simulation of application scheduling. In:
IEEE/ACM INTL. SYMP. ON CLUSTER COMPUTING AND THE GRID (CCGRID),
1., 2001. Proceedings... [S.l.: s.n.], 2001.

76
CASANOVA, H.; LEGRAND, A.; QUINSON, M. SimGrid: a generic framework for
large-scale distributed experiments. In: IEEE INTL. CONF. ON COMPUTER MODE-
LING AND SIMULATION, 10., 2008. Proceedings... [S.l.: s.n.], 2008.
CHIEN, A.; CALDER, B.; ELBERT, S.; BHATIA, K. Entropia: architecture and per-
formance of an enterprise desktop grid system. Journal of Parallel and Distributed
Computing, [S.l.], v.63, p.597–610, 2003.
CHOI, S.; KIM, H.; BYUN, E.; BAIK, M.; KIM, S.; PARK, C.; HWANG, C. Charac-
terizing and Classifying Desktop Grid. In: CLUSTER COMPUTING AND THE GRID,
2007. CCGRID 2007. SEVENTH IEEE INTERNATIONAL SYMPOSIUM ON, 2007.
Anais... [S.l.: s.n.], 2007. p.743 –748.
DEPOORTER, W.; MOOR, N.; VANMECHELEN, K.; BROECKHOVE, J. Scalability
of Grid Simulators: an evaluation. In: INTL. EURO-PAR CONF. ON PARALLEL PRO-
CESSING, 14., 2008. Proceedings... [S.l.: s.n.], 2008.
ESTRADA, T.; FLORES, D. A.; TAUFER, M.; TELLER, P. J.; KERSTENS, A.; AN-
DERSON, D. P. The Effectiveness of Threshold-Based Scheduling Policies in BOINC
Projects. In: SECOND IEEE INTL. CONF. ON E-SCIENCE AND GRID COMPUTING
(E-SCIENCE), 2006. Proceedings... [S.l.: s.n.], 2006.
ESTRADA, T.; TAUFER, M.; ANDERSON, D. Performance Prediction and Analysis of
BOINC Projects: an empirical study with emboinc. Journal of Grid Computing, [S.l.],
v.7, p.537–554, 2009.
ESTRADA, T.; TAUFER, M.; REED, K.; ANDERSON, D. P. EmBOINC: an emulator
for performance analysis of boinc projects. In: WORKSHOP ON DESKTOP GRIDS
AND VOLUNTEER COMPUTING SYSTEMS (PCGRID), 3., 2009. Proceedings...
[S.l.: s.n.], 2009.
FOSTER, I.; KESSELMAN, C.; TUECKE, S. The Anatomy of the Grid: enabling scala-
ble virtual organizations. Lecture Notes in Computer Science, [S.l.], v.2150, 2001.
HEIEN, E.; ANDERSON, D.; HAGIHARA, K. Computing Low Latency Batches with
Unreliable Workers in Volunteer Computing Environments. Journal of Grid Computing,
[S.l.], v.7, p.501–518, 2009.
HEIEN, E. M.; FUJIMOTO, N.; HAGIHARA, K. Computing low latency batches with
unreliable workers in volunteer computing environments. In: INTL. PARALLEL AND
DISTRIBUTED PROCESSING SYMP. (IPDPS), 2008. Proceedings... [S.l.: s.n.], 2008.
KONDO, D. SimBOINC: a simulator for desktop grids and volunteer computing sys-
tems. Acessado em Novembro 2010., http://simboinc.gforge.inria.fr/.
KONDO, D.; ANDERSON, D. P.; MCLEOD, J. V. Performance Evaluation of Sche-
duling Policies for Volunteer Computing. In: IEEE INTERNATIONAL CONFERENCE
ON E-SCIENCE AND GRID COMPUTING E-SCIENCE’07, 3., 2007, Bangalore, India.
Proceedings... [S.l.: s.n.], 2007.

77
KONDO, D.; ARAUJO, F.; MALECOT, P.; DOMINGUES, P.; SILVA, L.; FEDAK, G.;
CAPPELLO, F. Characterizing Result Errors in Internet Desktop Grids. In: KERMAR-
REC, A.-M.; BOUGé, L.; PRIOL, T. (Ed.). Euro-Par 2007 Parallel Processing. [S.l.]:
Springer Berlin / Heidelberg, 2007. p.361–371. (Lecture Notes in Computer Science,
v.4641).
KONDO, D.; CHIEN, A. A.; CASANOVA, H. Scheduling Task Parallel Applications for
Rapid Application Turnaround on Enterprise Desktop Grids. Journal of Grid Compu-
ting, [S.l.], v.5, n.4, 2007.
KONDO, D.; FEDAK, G.; CAPPELLO, F.; CHIEN, A. A.; CASANOVA, H. Characteri-
zing Resource Availability in Enterprise Desktop Grids. Journal of Future Generation
Computer Systems, [S.l.], v.23, n.7, 2007.
KONDO, D.; JAVADI, B.; IOSUP, A.; EPEMA, D. The Failure Trace Archive: ena-
bling comparative analysis of failures in diverse distributed systems. In: IEEE INT.
SYMP. ON CLUSTER COMPUTING AND THE GRID (CCGRID), 2010. Procee-
dings... [S.l.: s.n.], 2010.
KONDO, D.; TAUFER, M.; BROOKS, C.; CASANOVA, H.; CHIEN, A. A. Characte-
rizing and Evaluating Desktop Grids: an empirical study. In: INTL. PARALLEL AND
DISTRIBUTED PROCESSING SYMP. (IPDPS), 2004. Proceedings... [S.l.: s.n.], 2004.
LEGRAND, A.; TOUATI, C. How to measure efficiency? In: INTERNATIONAL
WORKSHOP ON GAME THEORY FOR COMMUNICATION NETWORKS (GAME-
COMM’07), 1., 2007. Proceedings... [S.l.: s.n.], 2007.
LEGRAND, A.; TOUATI, C. Non-Cooperative Scheduling of Multiple Bag-of-Task
Appplications. In: CONFERENCE ON COMPUTER COMMUNICATIONS (INFO-
COM’07), 25., 2007, Alaska, USA. Proceedings... [S.l.: s.n.], 2007.
LOW, S. H. A Duality Model of TCP and Queue Management Algorithms. IEEE/ACM
Transactions on Networking, [S.l.], v.11, n.4, 2003.
LUCE, R. D.; RAIFFA, H. Games and decisions : introduction and critical survey. [S.l.]:
Wiley, New York :, 1957. 509 p. :p.
MOWBRAY, M.; BRASILEIRO, F.; ANDRADE, N.; SANTANA, J.; CIRNE, W. A
Reciprocation-Based Economy for Multiple Services in Peer-to-Peer Grids. In: SIXTH
IEEE INTL. CONF. ON PEER-TO-PEER COMPUTING (P2P), 2006, Washington, DC,
USA. Proceedings... IEEE Computer Society, 2006.
MYERSON, R. B. Game theory: analysis of conflict. [S.l.]: Harvard University Press,
1997.
NAICKEN, S.; BASU, A.; LIVINGSTON, B.; RODHETBHAI, S. Towards Yet Another
Peer-to-Peer Simulator. In: HET-NETS, 2006. Proceedings... [S.l.: s.n.], 2006.
NASH, J. Equilibrium Points in N-Person Games. Proceedings of the National Aca-
demy of Sciences, [S.l.], v.36, n.1, p.48–49, 1950.
NASH, J. Non-Cooperative Games. The Annals of Mathematics, [S.l.], v.54, n.2, p.286–
295, 1951.

78
NISAN, N.; ROUGHGARDEN, T.; TARDOS, E.; VAZIRANI, V. V. Algorithmic Game
Theory. New York, NY, USA: Cambridge University Press, 2007.
NURMI, D.; BREVIK, J.; WOLSKI, R. Modeling Machine Availability in Enterprise
and Wide-area Distributed Computing Environments. In: INTL. EURO-PAR CONF. ON
PARALLEL PROCESSING, 2005. Proceedings... [S.l.: s.n.], 2005.
RILEY, G. F. The Georgia Tech Network Simulator. In: ACM SIGCOMM WORKSHOP
ON MODELS, METHODS AND TOOLS FOR REPRODUCIBLE NETWORK RESE-
ARCH, 2003. Proceedings... [S.l.: s.n.], 2003.
ROUGHGARDEN, T. Selfish Routing and the Price of Anarchy. [S.l.]: The MIT Press,
2005.
SANTOS-NETO, E.; CIRNE, W.; BRASILEIRO, F.; LIMA, A. Exploiting Replica-
tion and Data Reuse to Efficiently Schedule Data-Intensive Applications on Grids. In:
WORKSHOP ON JOB SCHEDULER STRATEGIES FOR PARALLEL PROCESSORS
(JSSPP), 2004. Proceedings... [S.l.: s.n.], 2004.
SHOCH, J. F.; HUPP, J. A. The wormprograms—early experience with a distributed
computation. Commun. ACM, New York, NY, USA, v.25, p.172–180, March 1982.
SILBERSTEIN, M.; SHAROV, A.; GEIGER, D.; SCHUSTER, A. GridBot: execution of
bags of tasks in multiple grids. In: CONFERENCE ON HIGH PERFORMANCE COM-
PUTING NETWORKING, STORAGE AND ANALYSIS, 2009, New York, NY, USA.
Proceedings... ACM, 2009. (SC ’09).
SILVA, F. A. B. da; SENGER, H. Improving scalability of Bag-of-Tasks applications
running on master-slave platforms. Parallel Computing, Amsterdam, The Netherlands,
The Netherlands, v.35, n.2, 2009.
STAINFORTH, D.; KETTLEBOROUGH, J.; ALLEN, M.; COLLINS, M.; HEAPS, A.;
MURPHY, J. Distributed computing for public-interest climate modeling research. Com-
puting in Science Engineering, [S.l.], v.4, n.3, p.82 –89, 2002.
STAINFORTH, D.; KETTLEBOROUGH, J.; MARTIN, A.; SIMPSON, A.; GILLIS, R.;
AKKAS, A.; GAULT, R.; COLLINS, M.; GAVAGHAN, D.; ALLEN, M. Climatepredic-
tion.net: design principles for public-resource modeling research. In: IN 14TH IASTED
INTERNATIONAL CONFERENCE PARALLEL AND DISTRIBUTED COMPUTING
AND SYSTEMS, 2002. Anais... [S.l.: s.n.], 2002. p.32–38.
STERLING, T.; BECKER, D. J.; SAVARESE, D.; DORBAND, J. E.; RANAWAKE,
U. A.; PACKER, C. V. BEOWULF: a parallel workstation for scientific computation. In:
IN PROCEEDINGS OF THE 24TH INTERNATIONAL CONFERENCE ON PARAL-
LEL PROCESSING, 1995. Anais... CRC Press, 1995. p.11–14.
TAUFER, M.; KERSTENS, A.; ESTRADA, T.; FLORES, D.; TELLER, P. J. SimBA: a
discrete event simulator for performance prediction of volunteer computing projects. In:
INTL. WORKSHOP ON PRINCIPLES OF ADVANCED AND DISTRIBUTED SIMU-
LATION (PADS), 21., 2007. Proceedings... [S.l.: s.n.], 2007.

79
THAIN, D.; TANNENBAUM, T.; LIVNY, M. Condor and the Grid. In: BERMAN, F.;
FOX, G.; HEY, T. (Ed.). Grid Computing: making the global infrastructure a reality.
[S.l.]: John Wiley Sons Inc., 2002.
The Failure Trace Archive. Acessado em Janeiro 2010., http://fta.inria.fr.
The SimGrid project. Acessado em Novembro 2010., http://simgrid.gforge.
inria.fr.
VELHO, P.; LEGRAND, A. Accuracy Study and Improvement of Network Simulation in
the SimGrid Framework. In: INTL. CONF. ON SIMULATION TOOLS AND TECHNI-
QUES (SIMUTOOLS), 2., 2009. Proceedings... [S.l.: s.n.], 2009.

81
APÊNDICE A
A.1 Influência do deadline e intervalo de conexão com réplicas
Este apêndice tem como objetivo verificar se o uso da replicação altera os valores
ótimos de prazo de término e intervalo de conexão que os projetos em rajadas devem
utilizar para obter o melhor desempenho possível da plataforma. A carga de trabalho é
composta por 4 projetos contínuos e 1 projeto em rajada, interagindo com um conjunto
de 1000 clientes cujos traços foram obtidos do projeto SETI@home. Ou seja, foram
utilizadas as mesmas configurações descritas nas Seções 5.1 e 5.2. A única diferença é o
uso de duas réplicas extras por tarefa, as quais, conforme a Seção 5.2.3, são o valor ótimo
para essa configuração.
A.1.1 Fixa
As Figuras A.1.a/b e A.2.a/b apresentam a equivalência a cluster quando não se utiliza
nenhuma estratégia de escalonamento. Como podemos ver, o intervalo de conexão não
influencia significativamente o CE de nenhum dos projetos (contínuos ou em rajadas).
Analisando o prazo de término, vemos que os valores máximos de CE para o projeto
em rajada são obtidos com um slack de aproximadamente σcste = 1.1, o mesmo obtido
anteriormente, e no qual o CErajada é igual a 136.
Já as Figuras A.1.c/d e A.2.c/d retratam a quantidade de tarefas perdidas pelos proje-
tos. O comportamento geral se manteve o mesmo, com um grande número de tarefas não
completadas pelos projetos em rajadas quando o prazo de término é curto. Isso, por sua
vez, causa o aumento da perda dos projetos contínuos. Entretanto, a replicação não au-
mentou a quantidade de tarefas perdidas de nenhum dos projetos na configuração ótima,
mantendo-a perto de 47.7% para os projetos em rajadas e 2.3% para os projetos contínuos.
A.1.2 Saturação
A forma das curvas do teste da política de saturação com o uso de réplicas manteve-se
o mesmo, como pode ser visto nas Figuras A.3 e A.4. A configuração ótima possui um
slack σcste = 1.1 do qual resulta um CErajada = 128 e CEcontnuo = 125 (utilizando um
intervalo de conexão de 2 horas). Nota-se que a replicação causou um pequeno aumento
no CE do projeto em rajada, 128 comparado a 122 sem réplicas. Consequentemente,
houve uma pequena retração no CE dos projetos contínuos, de 125 para 123. A perda de
tarefas se manteve praticamente constante, alcançando Wrajada = 10.7 para os projetos
em rajadas e Wcontnuos = 2.1 para os contínuos.

82
A.1.3 EDF
Da mesma forma que as duas estratégias citadas acima, a replicação não alterou sig-
nificativamente os resultados da política de seleção de tarefas EDF (Figuras A.5 e A.6).
O intervalo de conexão pouco modificou o CE dos projetos e foi fixado em 2 horas.
O slack ótimo é σcste = 1.1 do qual resulta nos seguintes valores: CErajada = 128,
Wrajada = 10.5, CEcontnuo = 123 e Wcontnuo = 2.1. É importante ressaltar que nova-
mente a política EDF não se mostrou superior à saturação para essa carga de trabalho,
entretanto acreditamos que com uma carga de trabalho mais diversa, composta por proje-
tos em rajadas com tamanhos e prazos de término variados, a política EDF possa resultar
em melhores resultados quando comparada às demais.

83
CE
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
108
110
112
114
116
118
120
CE
Deadline (h)
Intervalo de Conexãao (h)
CE
108
110
112
114
116
118
120
(1.a)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
50
60
70
80
90
100
110
120
130
140
CE
Deadline(h)
Intervalo de Conexãao(h)
CE
50
60
70
80
90
100
110
120
130
140
(1.b)
Perda
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0.023
0.024
0.025
0.026
0.027
0.028
0.029
0.03
0.031
0.032
0.033
Waste
Deadline(h)
Waste
0.023
0.024
0.025
0.026
0.027
0.028
0.029
0.03
0.031
0.032
0.033
(1.c)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
0.5
1
1.5
2
Waste
Deadline(h)
Waste
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
(1.d)
Figura A.1: Análise da influência do prazo de término e do intervalo de conexão no CE e
na perda, usando a estratégia de escalonamento fixa e 2 réplicas extras por tarefa.
CE
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
108
110
112
114
116
118
120
CE
Deadline (h)
CE
108
110
112
114
116
118
120
(2.a)
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
50
60
70
80
90
100
110
120
130
140
CE
Deadline(h)
CE
50
60
70
80
90
100
110
120
130
140
(2.b)
Perda
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0.023
0.024
0.025
0.026
0.027
0.028
0.029
0.03
0.031
0.032
0.033
Waste
Deadline(h)
Waste
0.023
0.024
0.025
0.026
0.027
0.028
0.029
0.03
0.031
0.032
0.033
(2.c)
0.4 0.6 0.8 1 1.2 1.4 1.6 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.5
1
1.5
2
Waste
Deadline(h)
Waste
0.4
0.6
0.8
1
1.2
1.4
1.6
(2.d)
na perda, usando a estratégia de escalonamento fixa e 2 réplicas extras por tarefa.

84
CE
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
122
124
126
128
130
132
134
136
138
CE
Deadline (h)
CE
122
124
126
128
130
132
134
136
138
(3.a)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(3.b)
Perda
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0.016
0.018
0.02
0.022
0.024
0.026
0.028
0.03
Waste
Deadline (h)
Waste
0.016
0.018
0.02
0.022
0.024
0.026
0.028
0.03
(3.c)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
Waste
Deadline (h)
Waste
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
(3.d)
na perda usando a estratégia de escalonamento saturação e 2 réplicas extras por tarefa.
CE
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
118
120
122
124
126
128
130
132
134
136
138
CE
Deadline (h)
CE
118
120
122
124
126
128
130
132
134
136
138
(4.a)
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(4.b)
Perda
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
0.024
0.025
Waste
Deadline (h)
Waste
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
0.024
0.025
(4.c)
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.2
0.4
0.6
0.8
1
Waste
Deadline (h)
Waste
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
(4.d)
na perda, usando a estratégia de escalonamento saturação e 2 réplicas extras por tarefa.

85
CE
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
110
115
120
125
130
135
140
CE
Deadline (h)
CE
110
115
120
125
130
135
140
(5.a)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(5.b)
Perda
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0.016
0.018
0.02
0.022
0.024
0.026
0.028
Waste
Deadline (h)
Waste
0.016
0.018
0.02
0.022
0.024
0.026
0.028
(5.c)
0 1 2 3 4 5 6 7 8 9 10 0
5
10
15
20
25
30
35
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
Waste
Deadline (h)
Waste
0
0.05
0.1
0.15
0.2
0.25
0.3
0.35
0.4
(5.d)
na perda, usando a estratégia de escalonamento EDF e 2 réplicas extras por tarefa.
CE
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
118
120
122
124
126
128
130
132
134
136
138
CE
Deadline (h)
CE
118
120
122
124
126
128
130
132
134
136
138
(6.a)
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
20
40
60
80
100
120
140
CE
Deadline (h)
CE
0
20
40
60
80
100
120
140
(6.b)
Perda
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
0.024
Waste
Deadline (h)
Waste
0.016
0.017
0.018
0.019
0.02
0.021
0.022
0.023
0.024
(6.c)
0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2 0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.1
0.2
0.3
0.4
0.5
0.6
Waste
Deadline (h)
Waste
0
0.1
0.2
0.3
0.4
0.5
0.6
(6.d)
na perda, usando a estratégia de escalonamento EDF e 2 réplicas extras por tarefa.

87
APÊNDICE B
B.1 Equilíbrios de Nash com diferentes números de clientes
Esta seção do apêndice visa apresentar mais alguns experimentos realizados na pro-
cura por equilíbrios de Nash no contexto dos sistemas BOINC. Foi variado o número de
clientes trabalhando para o conjunto de projetos, de forma a verificar que o fenômeno
ocorre em escalas maiores ou menores do sistema. A carga de trabalho foi mantida com
8 projetos, todos utilizando o teste de saturação como política de envio de tarefas, dos
quais:
• 1 projeto contínuo cujas tarefas correspondem às características do projeto SETI@home,
ou seja, 30 horas de cálculo e 300 horas de prazo de término;
• 7 projetos em rajadas cujas tarefas levam 1 hora para serem executadas.
Para cada conjunto de clientes, variou-se o número de tarefas de cada lote e é claro, o
prazo de término utilizado para os projetos em rajadas. Mais uma vez, o intervalo de
conexão é de 2 horas e os clientes utilizam traços de usuários reais do SETI@home,
disponíveis através do projeto FTA (The Failure Trace Archive, 2011).
Os resultados obtidos se assemelham àqueles da Seção 5.4, nos quais os equilíbrios
de Nash encontrados eram, de fato, Pareto ineficazes. Estes corroboram a necessidade
de um estudo mais aprofundado sobre consequências da otimização não cooperativa dos
projetos em rajadas.
B.1.1 100 Clientes
Para o ambiente com apenas 100 clientes, foram usados lotes com 50 tarefas por
dia. Com os jogadores utilizando uma estratégia de melhor resposta, encontrou-se um
equilíbrio de Nash com um slack de 2.2 (CErajada = 3.7 e CEcontnuo = 35.7). Por outro
lado, examinando a Figura B.3, o CE pode alcançar 4.2 caso os projetos escolhessem um
prazo de término de 1.25 horas (veja ponto 1 na figura). Ou ainda, com um slack de 1.1
(ponto 2 na figura), obter um CErajada = 4.1 e CEcontnuo = 38.9.
A Figura B.1 mostra, mais uma vez, que os projetos em rajadas têm um incentivo forte
de alterar seu slack quando se encontram com o deadline curto. Ainda, esse incentivo vai
diminuindo à medida que o prazo se encontra perto do NE. Por fim, percebe-se, através da
Figura B.2, que a estratégia da melhor resposta tende a convergir ao equilíbrio de Nash.
Além disso, é possível notar que quando os projetos em rajadas possuem um slack maior
que o NE a melhor resposta é diminuí-lo, assim como, quando ele é menor que o NE,
tende-se a aumentá-lo.

88
Equilíbrio de Nash
Consenso
Burst Dissidente
2
3
4
5
6
7
8
9
10
1 1.11.21.31.41.51.61.71.81.9 2 2.12.22.32.42.52.62.72.82.9 3 3.13.23.33.43.5
CE
Deadline (h)
Figura B.1: 100 clientes, 50 tarefas. Ilustrando o incentivo de um projeto alterar seu
deadline a partir de um estado de consenso. A linha de consenso representa o CE CEcons
de cada projeto em rajada se eles concordam com um certo deadline σcons. A linha di-
vergente representa quando um projeto dissidente pode melhorar seu CEdis selecionando
um deadline diferente σdis. O impacto de tal modificação da estratégia no CE dos demais
projetos é representada pela linha CEnao−dis.
Trajetória cíclica
Trajetória convergente
1
1.5
2
2.5
3
3.5
1 1.5 2 2.5 3 3.5
Deadline − Base
Deadline
−
Tendência
Figura B.2: 100 clientes, 50 tarefas. Esta figura retrata para um determinado σcons, a
tendência de resposta de σdis dos projetos em rajadas. Com tal informação, é possível ver
o resultado da estratégia de melhor resposta.

89
NE
Ponto 2
Ponto 1
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
1.4
1.45
1.5
1.55
1.6
1.65
1.7
1.75
1.8
1.85
1.9
1.95
2
2.05
2.1
2.15
2.2
2.25
2.3
2.35
2.4
2.45
2.5
2.55
2.6
2.65
2.7
2.75
2.8
2.85
2.9
2.95
3
3.05
3.1
3.15
3.2
3.25
3.3
3.35
3.4
3.45
3.5
35
35.5
36
36.5
37
37.5
38
38.5
39
39.5
3.5 3.6 3.7 3.8 3.9 4 4.1 4.2 4.3
CE − Burst
CE
−
Contínuos
Figura B.3: 100 clientes, 50 tarefas. Amostrando o conjunto de utilidade e ilustrando
a ineficiência do equilíbrio de Nash. 1 projeto contínuo e 7 projetos em rajadas com 50
tarefas de 1 hora por dia. CE pode ser melhorado em mais de 12% para os projetos em
rajadas caso seja escolhido, colaborativamente, σcons = 1.25 ao invés do NE (σNE =
2.2).
B.1.2 500 Clientes
Na configuração com 500 clientes foram utilizados lotes com 300 tarefas por dia. O
resultado dos testes indicou a existência de 2 equilíbrios de Nash, com slacks de 2.45 e 2.5.
No ponto 2.45, foram obtidos CErajada = 18.46 e CEcontnuo = 152.31. Já com σNE =
2.5, temos CErajada = 18.28 e CEcontnuo = 152.36. A Figura B.6 amostra o conjunto
de utilidade nessa configuração. É possível ver uma série de pontos que dominam os 2
pontos dos equilíbrios de Nash, e portanto, devem ser preferência de escolha frente aos
demais. Para ilustrar, um slack de 1.25 (ponto de referência), aumenta o CE dos projetos
em rajadas para 20.28, enquanto um prazo de término próximo de 1 hora leva a um CE de
quase 170 para os projetos contínuos.
A Figura B.5 ilustra dois pontos iniciais que levam a equilíbrios de Nash diferentes.
Ainda, o sistema converge rapidamente para os equilíbrios, independente do ponto de
começo. A Figura B.4 reforça a tendência dos projetos em rajadas de se afastarem dos
slacks curtos (próximos de 1.1), nos quais o sistema como um todo teria um melhor
desempenho.
B.1.3 2000 Clientes
Por fim, foram realizados testes com um número maior de clientes interagindo com o
mesmo conjunto de projetos (7 projetos em rajadas e 1 projeto contínuo). Selecionou-se
um subconjunto de 2000 usuários do projeto SETI@home e lotes de 1200 tarefas por dia.
De forma muito similar aos resultados anteriores, encontrou-se um equilíbrio de Nash
com prazo de término de 2.45 horas. Os CEs obtidos nesse caso são aproximadamente
iguais a CErajada = 74.8 e CEcontnuo = 634.9. Conforme é possível visualizar na Fi-
gura B.7, indicados nos pontos 1 e 2, o CE pode ser consideravelmente melhorado (mais
de 10%) para o projeto em rajada ou para o projeto contínuo caso fossem escolhidos os
slacks iguais a 1 ou 1.25.
Além disso, pode-se ver nas Figuras B.8 e B.9, o incentivo e a tendência dos projetos
em rajadas a convergirem rapidamente para o equilíbrio de Nash, reforçando portanto, a

90
Equilíbrios de Nash
Consenso
Burst Dissidente
10
15
20
25
30
35
40
45
50
55
1 1.11.21.31.41.51.61.71.81.9 2 2.12.22.32.42.52.62.72.82.9 3 3.13.23.33.43.5
CE
Deadline (h)
Trajetórias
Convergentes
1
1.5
2
2.5
3
3.5
1 1.5 2 2.5 3 3.5
Deadline − Base
Deadline
−
Tendência

91
NEs
Ponto de referência
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
1.4
1.45
1.5
1.55
1.6
1.65
1.7
1.75
1.8
1.85
1.9
1.95
2
2.05
2.1
2.15
2.2
2.25
2.3
2.35
2.4
2.45
2.5
2.55
2.6
2.65
2.7
2.75
2.8
2.85
2.9
2.95
3
3.05
3.1
3.15
3.2
3.25
3.3
3.35
3.4
3.45
3.5
145
150
155
160
165
170
17 17.5 18 18.5 19 19.5 20 20.5
CE − Burst
CE
−
Contínuos
2.5).
necessidade do estudo cuidadoso das perdas ocorridas pelo comportamento egoísta dos
projetos.

92
NE
Ponto 2
Ponto 1
1
1.05
1.1
1.15
1.2
1.25
1.3
1.35
1.4
1.45
1.5
1.55
1.6
1.65
1.7
1.75
1.8
1.85
1.9
1.95
2
2.05
2.1
2.15
2.2
2.25
2.3
2.35
2.4
2.45
2.5
2.55
2.6
2.65
2.7
2.75
2.8
2.85
2.9
2.95
3
3.05
3.1
3.15
3.2
3.25
3.3
3.35
3.4
3.45
3.5
620
630
640
650
660
670
680
690
700
710
68 70 72 74 76 78 80 82 84 86
CE − Burst
CE
−
Contínuos
2.45).
Equilíbrio de Nash
Consenso
Burst Dissidente
40
60
80
100
120
140
160
180
200
1 1.11.21.31.41.51.61.71.81.9 2 2.12.22.32.42.52.62.72.82.9 3 3.13.23.33.43.5
CE
Deadline (h)

93
Convergente
Trajetória
1
1.5
2
2.5
3
3.5
1 1.5 2 2.5 3 3.5
Deadline − Base
Deadline
−
Tendência

ANÁLISE DE COMPORTAMENTO NÃO COOPERATIVO EM COMPUTAÇÃO VOLUNTÁRIA

Mais conteúdo relacionado

Semelhante a ANÁLISE DE COMPORTAMENTO NÃO COOPERATIVO EM COMPUTAÇÃO VOLUNTÁRIA

Mais de Jerbialdo

ANÁLISE DE COMPORTAMENTO NÃO COOPERATIVO EM COMPUTAÇÃO VOLUNTÁRIA