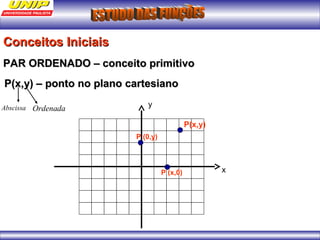
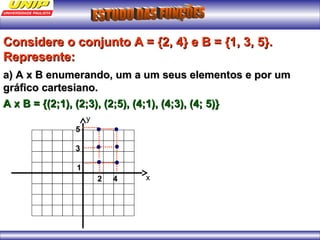
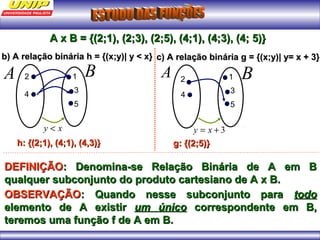
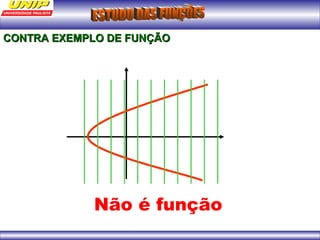
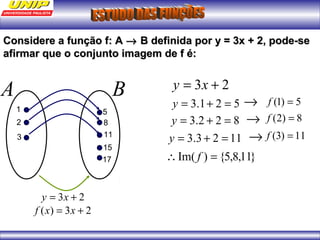
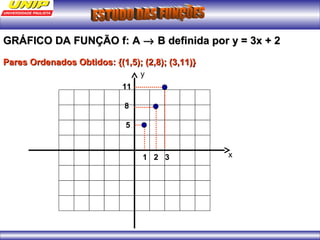
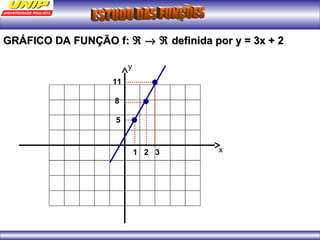
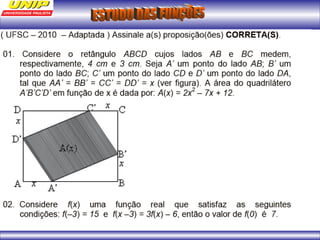
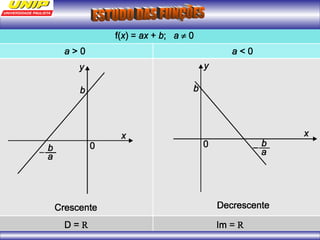
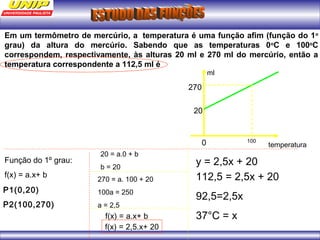
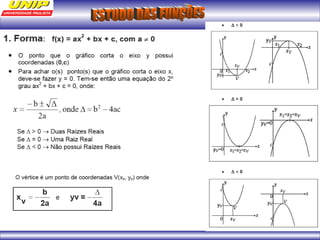
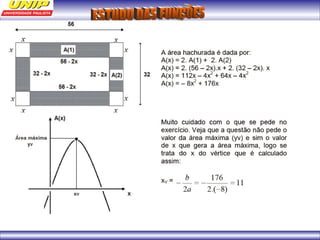
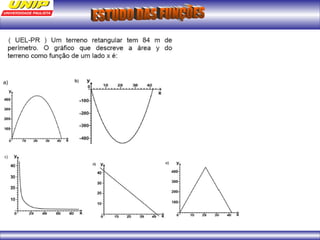
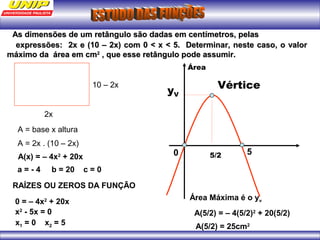
(1) A função representa o custo de produção C em reais de n quilos de um produto. (2) Se o produto for vendido a R$102 o quilo, a porcentagem de lucro será de 20%. (3) Uma depreciação linear no preço de um moinho ao longo de 6 anos é representada por uma função afim.

2. CCoonncceeiittooss IInniicciiaaiiss
PPAARR OORRDDEENNAADDOO –– ccoonncceeiittoo pprriimmiittiivvoo
PP((xx,,yy)) –– ppoonnttoo nnoo ppllaannoo ccaarrtteessiiaannoo
Abscissa Ordenada
P(x,y)
P (x,0)
P (0,y)
x
y

3. PPrroodduuttoo CCaarrtteessiiaannoo
DDaaddooss ddooiiss ccoonnjjuunnttooss AA ee BB,, ddeennoommiinnaa--ssee pprroodduuttoo ccaarrtteessiiaannoo
ddee AA ppoorr BB aaoo ccoonnjjuunnttoo ffoorrmmaaddoo ppoorr ppaarreess oorrddeennaaddooss ((xx;;yy))
ttaaiiss qquuee xx Î AA ee yy Î BB..
NNOOTTAAÇÇÃÃOO:: AA xx BB == {{((xx,, yy)) || xx Î AA ee yy Î BB}}

4. Considere o conjunto AA == {{22,, 44}} ee BB == {{11,, 3,, 55}}..
RReepprreesseennttee::
aa)) AA xx BB eennuummeerraannddoo,, uumm aa uumm sseeuuss eelleemmeennttooss ee ppoorr uumm
ggrrááffiiccoo ccaarrtteessiiaannoo..
AA xx BB == {{((22;;11)),, ((22;;3)),, ((22;;55)),, ((44;;11)),, ((44;;3)),, ((44;; 55))}}
2 4
5
3
1
x
y

5. AA xx BB == {{((22;;11)),, ((22;;3)),, ((22;;55)),, ((44;;11)),, ((44;;3)),, ((44;; 55))}}
b) A relação binária hh == {{((xx;;yy))|| yy << xx}}
A B 2
y < x
4
1
3
5
hh:: {{((22;;11)),, ((44;;11)),, ((44,,3))}}
cc)) AA rreellaaççããoo bbiinnáárriiaa gg == {{((xx;;yy))|| yy== xx ++ 3}}
A B
y = x + 3
2
4
1
3
5
gg:: {{((22;;55))}}
DDEEFFIINNIIÇÇÃÃOO:: DDeennoommiinnaa--ssee RReellaaççããoo BBiinnáárriiaa ddee AA eemm BB
qquuaallqquueerr ssuubbccoonnjjuunnttoo ddoo pprroodduuttoo ccaarrtteessiiaannoo ddee AA xx BB..
OOBBSSEERRVVAAÇÇÃÃOO:: QQuuaannddoo nneessssee ssuubbccoonnjjuunnttoo ppaarraa ttooddoo
eelleemmeennttoo ddee AA eexxiissttiirr uumm úúnniiccoo ccoorrrreessppoonnddeennttee eemm BB,,
tteerreemmooss uummaa ffuunnççããoo ff ddee AA eemm BB..

6. c) A relação binária f == {{((xx;;yy))|| yy == xx ++ 11}}
A B 2
y = x +1
4
1
3
5
ff:: {{((22;;3)),, ((44;;55))}}
ff éé uummaa ffuunnççããoo ddee AA eemm BB,, ppooiiss ttooddoo
eelleemmeennttoo ddee AA eessttáá aassssoocciiaaddoo aa uumm úúnniiccoo
eelleemmeennttoo eemm BB
EELLEEMMEENNTTOOSS DDEE UUMMAA FFUUNNÇÇÃÃOO:: ff:: AA ® BB
DDOOMMÍÍNNIIOO:: AA == {{22,, 44}}
CCOONNTTRRAA DDOOMMÍÍNNIIOO:: BB == {{11,, 3,, 55}}
CCOONNJJUUNNTTOO IIMMAAGEEMM:: IImm ((ff)) == {{3,, 55}}

7. CCOONNTTRRAA EEXXEEMMPPLLOO DDEE FFUUNNÇÇÃÃOO
Não é função

8. Considere aa ffuunnççããoo ff:: AA ® BB ddeeffiinniiddaa ppoorr yy == 3xx ++ 22,, ppooddee--ssee
aaffiirrmmaarr qquuee oo ccoonnjjuunnttoo iimmaaggeemm ddee ff éé::
A B y = 3x + 2
y = 3.1+ 2 = 5 1
2
3
y = 3x + 2
5
8
11
15
17
y = 3.2 + 2 = 8
y = 3.3 + 2 = 11
f (x) = 3x + 2
®
®
®
f (1) = 5
f (2) = 8
f (3) = 11
Im( f ) = {5,8,11}

9. GRÁFICO DDAA FFUUNNÇÇÃÃOO ff:: AA ® BB ddeeffiinniiddaa ppoorr yy == 33xx ++ 22
PPaarreess OOrrddeennaaddooss OObbttiiddooss:: {{((11,,55);; ((22,,88);; ((33,,1111)}}
1 2 3
11
8
5
x
y

10. GGRRÁÁFFIICCOO DDAA FFUUNNÇÇÃÃOO ff:: Â ® Â ddeeffiinniiddaa ppoorr yy == 33xx ++ 22
1 2 3
11
8
5
x
y

11. Seja o gráfico abaixo da função f, determinar a soma dos números associados às
proposições VERDADEIRAS:
01. O domínio da função f é {x Î R | - 3 £ x £ 3}
02. A imagem da função f é {y Î R | - 2 £ y £ 3}
04. para x = 3, tem-se y = 3
08. para x = 0, tem-se y = 2
16. para x = - 3, tem-se y = 0
32. A função é decrescente em todo seu domínio
V
V
(3,3) ou f(3) = 3
(0,2) ou f(0) = 2
(-3,2) ou f(-3) = 2
VVFF

14. Resposta: a = 20000 e b = 2

15. Resposta: 12

17. ( UFSC ) Seja f(x) = ax + b uma função linear. Sabe-se que f(-1) = 4 e
f(2) = 7. Dê o valor de f(8).
f(-1) = 4
f(2) = 7
(-1, 4)
(2, 7)
y = ax + b
- a b 4
4 = a(-1) + b
7 = a(2) + b î í ì
+ =
2a + b =
7
a = 1 b = 5
f(x) = ax + b
f(x) = 1.x + 5
f(x) = x + 5
Logo:
f(8) = 8 + 5
f(8) = 13

18. A semi-reta representada no gráfico seguinte expressa o custo de produção C, em
reais, de n quilos de certo produto.
C(reais)
80
0 20 x(quilogramas)
180
Se o fabricante vender esse
produto a R$ 102,00 o quilo,
a sua porcentagem de lucro
em cada venda será?
Função do 1º grau:
f(x) = a.x+ b
P1(0,80)
P2(20,180)
80 = a.0 + b
b = 80
180 = a. 20 + 80
20a = 100
a = 5
f(x) = a.x+ b
f(x) = 5.x+ 80
f(1) = 5.1+ 80 Þ ff((11)) == 8855
R$ 85 Û 100%
R$102 Û x
x = 120%
LUCRO DE 20%

20. Um camponês adquire um moinho ao preço de R$860,00. Com o passar do tempo,
ocorre uma depreciação linear no preço desse equipamento. Considere que, em 6 anos,
o preço do moinho será de R$ 500,00. Com base nessas informações, é correto afirmar:
x(anos)
y(reais)
A
0 6
860
500
Função do 1º grau:
f(x) = a.x+ b
A(0,860)
B(6,500)
860 = a.0 + b
b = 860
500 = a. 6 + 860
-360 = 6a
a = -60
f(x) = a.x+ b
f(x) = -60.x+ 860
a) f(3) = -60.3+ 860
f(3) = 680
B
F
b) f(9) = -60.9+ 860
f(9) = 320
F
c) f(7) = -60.7+ 860
f(7) = 440
F
d) - 60x + 860 < 200
-60x < -660
x > 11anos
F
e) f(13) = -60.13+ 860
f(13) = 440
f(13) = 80
V

21. Em um termômetro de mercúrio, a temperatura é uma função afim (função do 1o
grau) da altura do mercúrio. Sabendo que as temperaturas 0oC e 100oC
correspondem, respectivamente, às alturas 20 ml e 270 ml do mercúrio, então a
temperatura correspondente a 112,5 ml é
ml
20
0 100 temperatura
270
Função do 1º grau:
f(x) = a.x+ b
P1(0,20)
P2(100,270)
20 = a.0 + b
b = 20
270 = a. 100 + 20
100a = 250
a = 2,5
f(x) = a.x+ b
f(x) = 2,5.x+ 20
y = 2,5x + 20
112,5 = 2,5x + 20
92,5=2,5x
37°C = x

22. Função do 1º grau:
y = f(x) = a.x+ b
GRÁFICO PASSA PELA ORIGEM
y = a.x
CÁLCULO DO COEFICIENTE ANGULAR
y = a.x
50 = a.40 ® a = 5/4
y a x
.
=
5
y x
.
4
=
30 5
x
=
=
24
.
4
g x

23. EXTRAS
01)
02)
RESPOSTA:

24. RESPOSTA: 0,2

26. Em relação a função f(x) = 2x2 – 12x + 16 definida de ® Â, determine:
a) sua intersecção com o eixo y
b) sua intersecção com o eixo x
c) seu vértice
d) Imagem da função
e) A área do triângulo cujos vértices são o vértice da parábola e seus zeros

29. a)

30. As pelaAs dimensões de um retângulo são dadas em centímetros, pelass
eexxpprreessssõõeess:: 22xx ee ((1100 –– 22xx)) ccoomm 00 << xx << 55.. DDeetteerrmmiinnaarr,, nneessttee ccaassoo,, oo vvaalloorr
mmááxxiimmoo ddaa áárreeaa eemm ccmm22 ,, qquuee eessssee rreettâânngguulloo ppooddee aassssuummiirr..
Vértice
5/2
yV
0 5
2x
10 – 2x
A = base x altura
A = 2x . (10 – 2x)
A(x) = – 4x2 + 20x
a = - 4 b = 20 c = 0
RAÍZES OU ZEROS DA FUNÇÃO
0 = – 4x2 + 20x
x2 - 5x = 0
x1 = 0 x2 = 5
Área
Área Máxima é o yv
A(5/2) = – 4(5/2)2 + 20(5/2)
A(5/2) = 25cm2