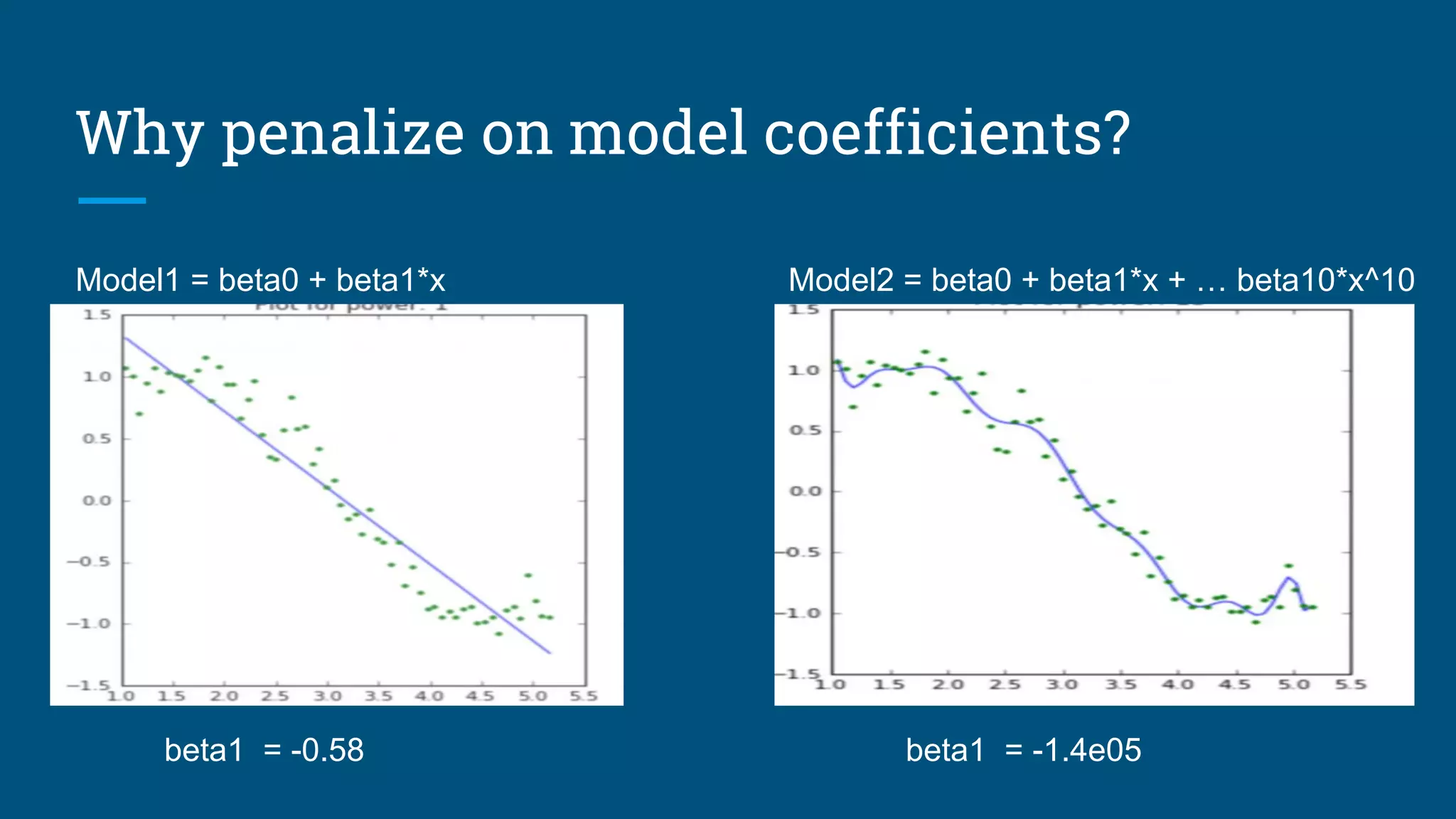
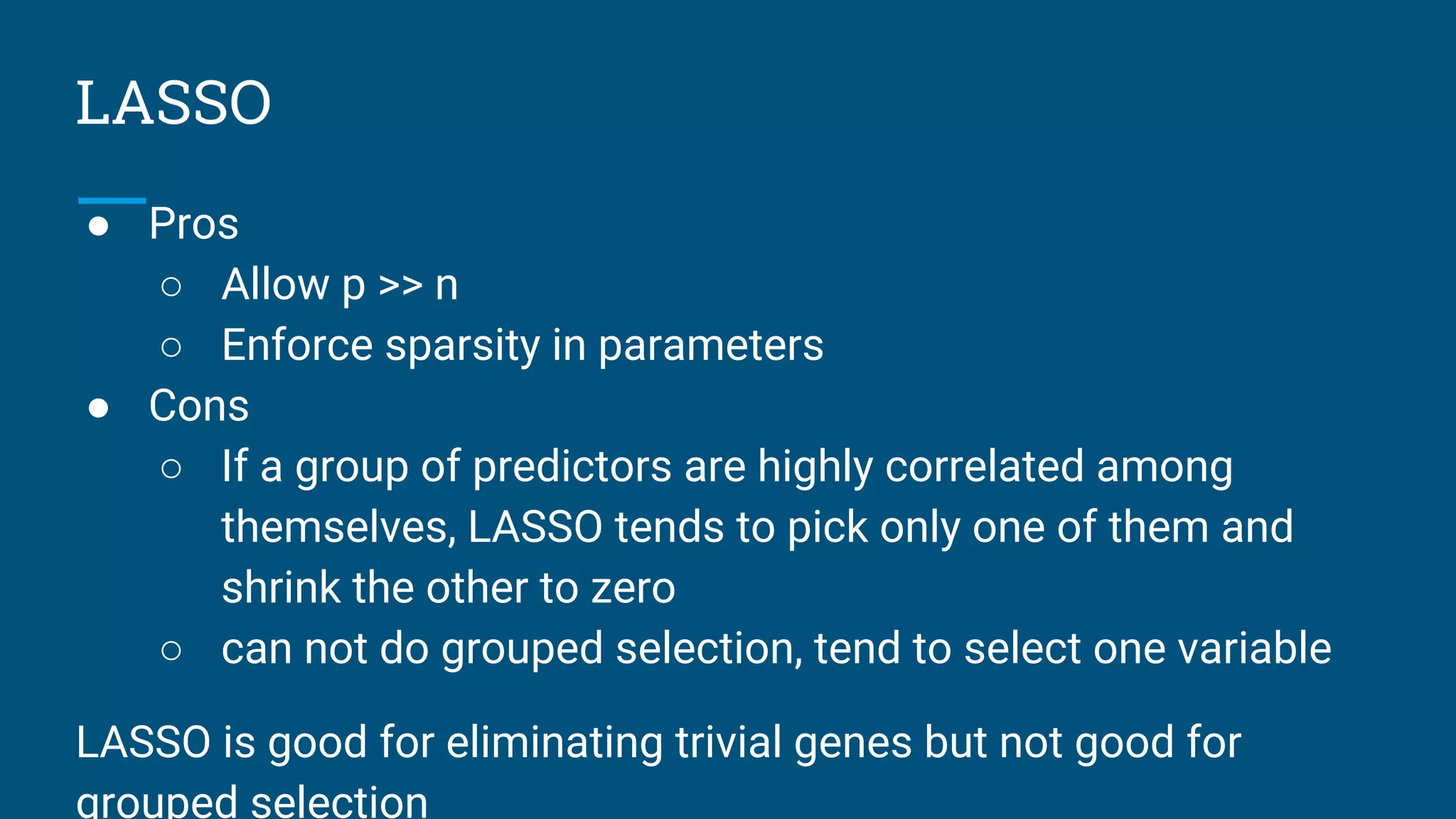
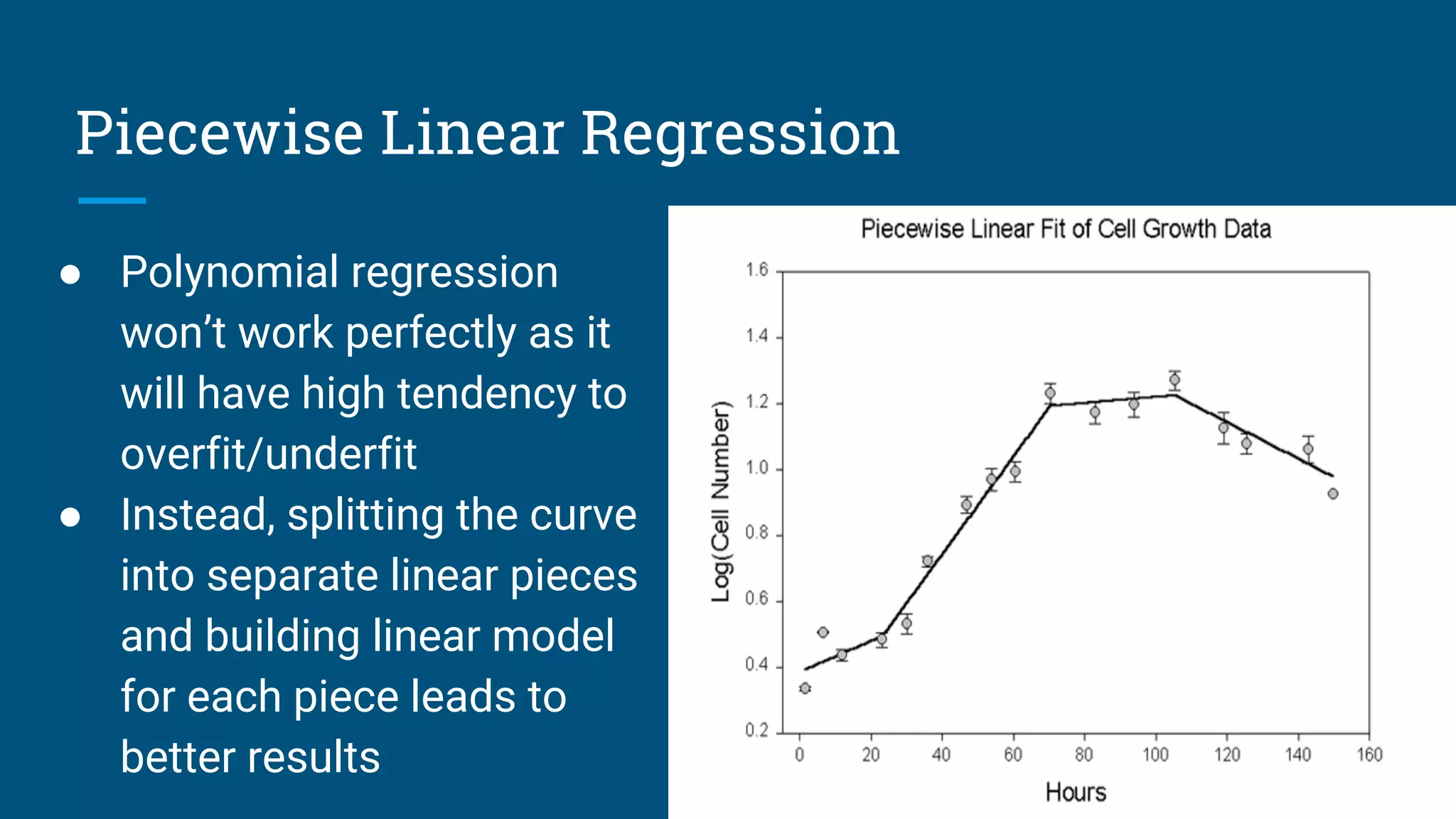
The document discusses various machine learning algorithms and model selection techniques, highlighting the advantages and disadvantages of each method, including Naive Bayes, logistic regression, decision trees, and SVM. It also covers advanced regression issues and regularization techniques, detailing ridge and lasso regression's pros and cons along with their applications in gene selection problems. Lastly, it introduces additional methods such as Poisson regression and piecewise linear regression for specific types of data.

1. Advanced Regression
and Model Selection
UpGrad Live Session - Ankit Jain

2. Model Selection Techniques
● If you are looking for a good place to start to choose a
machine learning algorithm for your dataset here are some
general guidelines.
● How large is your training set?
○ Small -- Prefer high bias/low variance classifiers (e.g.
Naive Bayes) over low bias/high variance classifiers (e.g.
KNN) to avoid overfitting.
○ Large - Low Bias/High Variance classifiers tend to produce
more accurate models

3. Adv/Disadv of Various Algorithms
● Naive Bayes:
○ Very simple to implement as it’s just a bunch of counts.
○ If conditional independence exists, it converges faster
than say Logistic Regression and thus requires less
training data.
○ If you want something fast,easy and performs well NB is a
good choice
○ Biggest disadvantage is that it can’t learn interactions in
the dataset

4. Adv/Disadv of Various Algorithms
● Logistic Regression:
○ Lots of ways to regularize the model and no need to worry
about features being correlated like in Naive Bayes.
○ Nice probabilistic interpretation. Helpful in problems like
churn prediction etc .
○ Online algorithm: Easy to update the model with the new
data (using an online gradient descent method)

5. Adv/Disadv of Various Algorithms
● Decision Trees:
○ Easy to explain and interpret (at least for some people)
○ Easily handles feature interactions.
○ No need to worry about outliers or whether data is linearly
separable or not.
○ Doesn’t support online learning. Rebuilding the model with
new data every time can be painful.
○ Tend to easily overfit. Solution: ensemble methods (RF)

6. Adv/Disadv of Various Algorithms
● SVM:
○ High accuracy for many datasets
○ With appropriate kernel, can work well even if your data
isn’t linearly separable in the base feature space.
○ Popular in text processing applications where high
dimensionality is a norm
○ Memory intensive, hard to interpret and kind of annoying
to run and tune

7. ADVANCED REGRESSION

8. Linear Regression Issues
● Sensitivity to outliers
● Multicollinearity leads to high variance of the estimator.
● Prone to overfit if there are lot of variables
● Hard to interpret when the number of predictors is large.Need
a smaller subset that exhibits strongest effects.

9. Regularization Techniques
● Regularization techniques typically work by penalizing the
magnitude of coefficients of features along with minimizing
the error between predicted and actual observations
● Different types of penalization
○ Ridge Regression: Penalize on squared coefficients
○ Lasso Regression: Penalize on absolute value of
coefficients

10. Why penalize on model coefficients?
Model1 = beta0 + beta1*x Model2 = beta0 + beta1*x + … beta10*x^10
beta1 = -0.58 beta1 = -1.4e05

11. Ridge Regression
● L2 penalty
● Pros
○ Variables >> Rows
○ Multicollinearity
○ Increased bias and lower variance from Linear Regression
● Cons
○ Doesn’t produce parsimonious model
Let’s see a collinearity example in R

12. Example: Luekemia Prediction
● Leukemia Data, Golub et al. Science 1999
● There are 38 training samples and 34 test samples with total
genes ~ 7000 (p >> n)
● Xij is the gene expression value for sample i and gene j
● Sample i either has tumor type AML or ALL
● We want to select genes relevant to tumor type
○ eliminate the trivial genes
○ grouped selection as many genes are highly correlated
● Ridge Regression can help to pursue this modeling

13. Grouped Selection
● If two predictors are highly correlated among themselves, the
estimated coefficients will be similar for them.
● if some variables are exactly identical, they will have same
coefficients
Ridge is good for grouped selection but not good for eliminating
trivial genes

14. LASSO
● Pros
○ Allow p >> n
○ Enforce sparsity in parameters
● Cons
○ If a group of predictors are highly correlated among
themselves, LASSO tends to pick only one of them and
shrink the other to zero
○ can not do grouped selection, tend to select one variable
LASSO is good for eliminating trivial genes but not good for
grouped selection

15. Elastic Net
● Weighted combination of L1 and L2 penalty
● Helps in enforcing sparsity
● Encourage grouping effect in highly correlated predictors
In gene selection problem, it can achieve both purposes of
removing trivial genes and doing group selection

16. Other Advanced Regression Methods
Poisson Regression
○ Typically used when the Y variable follows poisson
distribution (typically counts of events within a time t)
○ # times a customer will visit an ecommerce website next
month

17. Piecewise Linear Regression
● Polynomial regression
won’t work perfectly as it
will have high tendency to
overfit/underfit
● Instead, splitting the curve
into separate linear pieces
and building linear model
for each piece leads to
better results

18. QUESTIONS