Projectile motion
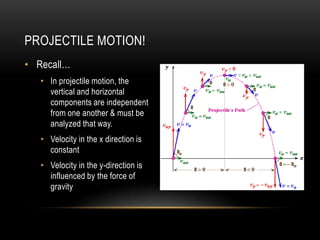
- 1. PROJECTILE MOTION! • Recall… • In projectile motion, the vertical and horizontal components are independent from one another & must be analyzed that way. • Velocity in the x direction is constant • Velocity in the y-direction is influenced by the force of gravity
- 2. VERTICALLY LAUNCHED PROJECTILES NO Vertical Velocity at the top of the trajectory. Vertical Vertical Velocity Velocity increases on the decreases way down, on the way upward Horizontal Velocity is constant Component Magnitude Direction Horizontal Constant Constant Vertical Decreases up, 0 Changes @ top, Increases down
- 3. VERTICALLY LAUNCHED PROJECTILES Since the projectile was launched at a angle, the velocity MUST be broken into components!!! Vxi = Vi cosθ vi vyi Vyi = Visinθ q vxi
- 4. VERTICALLY LAUNCHED PROJECTILES There are several things you must consider when doing these types of projectiles besides using components. If it begins and ends at ground level, the “y” displacement is ZERO: y = 0
- 5. VERTICALLY LAUNCHED PROJECTILES You will still use kinematic equations, but YOU MUST use COMPONENTS in the equation. vi vyi X = Vxi t yf = yi + Vyit+0.5gt2 q vxi Vxi = Vi cosθ Vyi = Visinθ
- 6. EXAMPLE A place kicker kicks a football with a velocity of 20.0 m/s and at an angle of 53 degrees. (a) How long is the ball in the air? (b) How far away does it land? 4 m/ s Step 1: Break initial velocity into (c) How high does it travel? Its vector components 7m/ s Vxi = Vi cosθ Vxi = 20cos53 = 12.04 m/s q 53 Vyi = Visinθ Vyi = 20sin53 = 15.97 m/s
- 7. EXAMPLE X y A place kicker kicks a xi 0m 0m football with a velocity of xf ? 0m 20.0 m/s and at an angle of 53 degrees. vi Vxi = 12.04 m/s Vyi =15.97 m/s (a) How long is the ball in the air? vf a 0 - 9.8 m/s/s yf = yi + Vyit+0.5gt2 t ? 0 = 0 + 15.97t + 0.5 (-9.8)t2 -15.97t = -4.9t2 -15.97 = -4.9 t t = 3.26 s
- 8. X y EXAMPLE xi 0m 0m A place kicker kicks a xf ? 0m football with a velocity of vi Vxi = 12.04 m/s Vyi =15.97 20.0 m/s and at an angle m/s of 53 degrees. (b) How far away does it vf land? a 0 - 9.8 m/s/s t 3.26s X = vxit (12.04)(3.26) = 39.24 m
- 9. X y EXAMPLE xi 0m 0m xf ? ? A place kicker kicks a football with a velocity of 20.0 m/s and vi Vxi = 12.04 m/s Vyi =15.97 m/s at an angle of 53 degrees. vf a 0 - 9.8 m/s/s (c) How high does it travel? t 3.26s ÷ 2 = 1.63 s CUT YOUR TIME IN HALF! yf = yi + Vyit+0.5gt2 yf = 0 + 15.97(1.26) + 0.5 (-9.8)(1.26)2 = 13.01 m
- 10. EXAMPLE: X y xi 0m 0m A soccer ball is kicked towards xf ? 0m the goal at 12 m/s at an angle vi 9.83 m/s 6.88 m/s of 35° from the ground, and just makes it into the goal. vf How far away was the player a 0 - 9.8 m/s/s from the goal when they t 1.40 s kicked the ball? 1. Write down all information & X = 13.8 m draw a diagram 2. Break Vi into its components 3. Use equations to solve for x.
- 12. TRAJECTORY AND RANGE • Maximum range is at 45° • Low and high trajectory cover the same distance. • 30 and 60 • 10 and 80 • 25 and…
- 14. THE RANGE EQUATION! • Range: Maximum horizontal distance of a projectile. • Equation is derived on page 64 in your book… X = R = 2Vo2sinθcosθ g Using the trig substitution 2sinθcosθ = sin2θ, we get… X = R = Vo2sin2θ g Vyi θ Vxi R
- 15. RANGE • When solving for theta (θ) using the range equation, you must solve for both complementary angles Complementary angles = θ or 90-θ