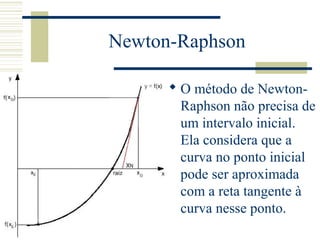
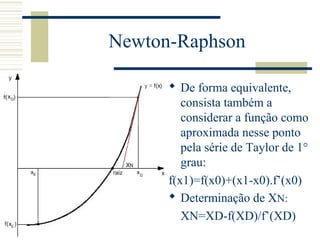
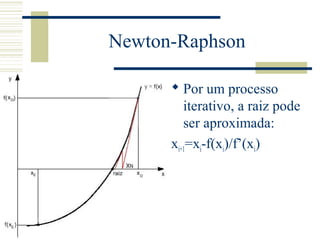
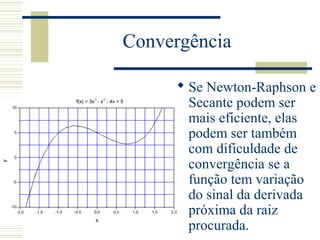
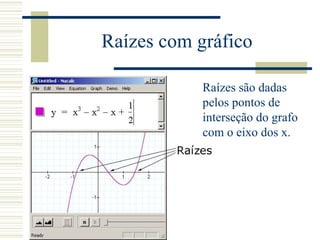
O documento discute métodos para determinar raízes de funções, incluindo métodos matemáticos exatos para polinômios de grau menor ou igual a 3, métodos gráficos usando interseção com o eixo x, e métodos numéricos como bisseção, secante e Newton-Raphson para aproximar raízes em casos gerais.

1. Zero de função

2. Problema
 O cálculo de raízes de funções encontra um
grande emprego na obtenção da solução de
uma vasta gama de problemas de engenharia.
 Em geral, trata-se de determinar o(s) valores
de x tal que f(x)=0, onde f é a função cujo
raízes são a determinar.

3. Métodos matemáticos
 A matemática fornece métodos formais que permite
a determinação exata das raízes em diversos casos.
 Os métodos mais conhecido permitem a
determinação de raízes de polinômios ate grau 3, ou
grau maior mais em certas condições.
 Em muitas situações, a resolução matemática
necessita de intuição para que elas sejam
transformadas em casos resolvíveis.

4. Exemplos
 Polinômios do primeiro e segundo grau ou
transformáveis em polinômios do primeiro
ou segundo grau:
 Funções cuja a recíproca é conhecida:
2
2
2 3 0; 3 5 0
2sin 3 0;sin 3sin 5 0
x x x
x x x
+ = + + =
+ = + + =
10log 5 0x − =

5. Determinação gráfica
 A representação gráfica de uma função é
uma fonte de informações úteis sobre o
comportamento da função, particularmente
para a determinação das raízes.
 Além disso, o grafo permite de compreender
o funcionamento dos métodos numéricos
para determinar as raízes.

6. Raízes com gráfico
Raízes são dadas
pelos pontos de
interseção do grafo
com o eixo dos x.

7. Métodos numéricos
 Mesmo com um método formal, o(s)
valor(es) calculado(s) pelo computador é
aproximado, a não seja usar um CAS.
 Existem métodos numéricos que permite
aproximar as raízes em casos gerais,
inclusivo casos que a matemática não resolva
de formalmente.

8. Métodos numéricos
 Vamos estudar três métodos de determinação
de raízes:
 Bisseção
 Secante
 Newton-Raphson

9. Bisseção
 Th: Se y=f(x) é uma função contínua e muda
de sinal no intervalo [a,b] (isto é se
f(a).f(b)<0), então existe pelo menos um
ponto x0 ∈ [a,b] tal que f(x0)=0.
 Além disso, se f’(x) não muda de sinal em
[a,b], x0 é a única raiz de f(x) nesse intervalo.

10. Bisseção
 Para se aproximar de uma raiz, o princípio da
bisseção consista em reduzir o intervalo
inicial testando o sinal de f(x) para o ponto
médio do intervalo.
 Considerando o intervalo [a,b]
 Se , o novo intervalo e [a,(a+b)/2]
 Se , o novo intervalo e [(a+b)/2,b]
( ). ( ) 0
2
a b
f a f
+
<
( ). ( ) 0
2
a b
f b f
+
<

11. Algoritmo
 Raiz(f,a,b,tol)
 Enquanto (|a-b|>tol)
 x=(a+b)/2
 Se f(x).f(a)<0
 b=x
 Senão
 a=x
 Resultado=(a+b)/2

12. Bisseção
 Esse método, com um bom escolhe do intervalo
inicial, é adaptado com a representação dos
números do computador: a divisão por 2 a cada
passo é uma operação simples.
 A convergência do algoritmo é garantida, o
algoritmo não saia do intervalo inicial, esse
intervalo é cada vez dividido por dois,
 A convergência é muito lenta: para ganhar uma
decimal (base 10), preciso de 3 a 4 passos.

13. Secante
 O método da secante funciona sobre o
mesmo princípio que a bisseção e necessita
da mesma condição inicial: continuidade da
função.

14. Secante
 Com esse método,
determinamos um ponto a
partir da assimilação da
curva com um segmento
passando pelos pontos
(XE, f(XE)) e (XD, f(YD)).
O candidato para ser raiz é
o ponto de interseção desse
segmento com o eixo x.

15. Secante
 Determinação de XN:
Temos a relação:
De onde podemos extrair XN:
( )
( )
D ND
E E N
X Xf X
f X X X
−
=
−
( ) ( )
( ) ( )
D E E D
N
D E
f X X f X X
X
f X f X
−
=
−

16. Secante
 O segmento (XN,f(XN));
(XD,f(XD)) é usado para
determinar o valor do
passo seguinte.

17. Algoritmo
 Raiz(f,a,b,iter)
 Repete iter vezes
 b=(b.f(a)-a.f(b))/(f(a)-f(b))
 Resultado=b

18. Falsa posição
 O método da falsa posição aparece como
uma combinação entre o método da secante e
a bisseção. As condições iniciais são as
mesma que no caso da bisseção (intervalo
onde a função troca de sinal).

19. Falsa posição
 Como no caso da secante,
determinamos um ponto a
partir da assimilação da
curva com um segmento
passando pelos pontos
(XE, f(XE)) e (XD, f(YD)).
 Temos:
( ) ( )
( ) ( )
D E E D
N
D E
f X X f X X
X
f X f X
−
=
−

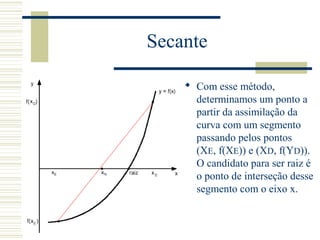
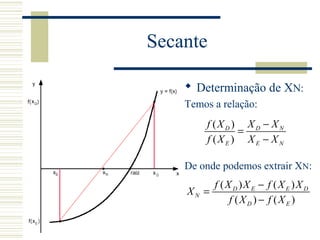
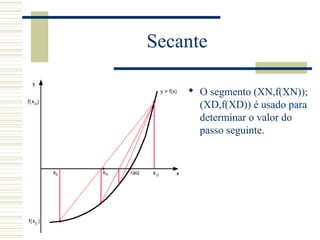
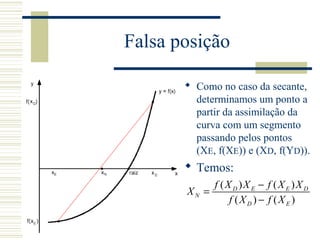
20. Falsa posição
 No caso da falsa posição, o
novo segmento é
determinado em função
dos sinais de f(XN)f(XD) e
f(XN)f(XE).
 Se f troca de sinal entre
XE e XN, o novo intervalo
é [XE, XN], senão o novo
intervalo é [XN, XE].

21. Algoritmo
 Raiz(f,a,b,iter)
 Repete iter vezes
 x=(b.f(a)-a.f(b))/(f(a)-f(b))
 Se f(x).f(a)<0, b=x
 Senão a=x
 Resultado=x

22. Newton-Raphson
 O método de Newton-
Raphson não precisa de
um intervalo inicial.
Ela considera que a
curva no ponto inicial
pode ser aproximada
com a reta tangente à
curva nesse ponto.

23. Newton-Raphson
 De forma equivalente,
consista também a
considerar a função como
aproximada nesse ponto
pela série de Taylor de 1°
grau:
f(x1)=f(x0)+(x1-x0).f’(x0)
 Determinação de XN:
XN=XD-f(XD)/f’(XD)

24. Newton-Raphson
 Por um processo
iterativo, a raiz pode
ser aproximada:
xi+1=xi-f(xi)/f’(xi)

25. Algoritmo
 Raiz(f,x0,iter)
 X=x0
 Repete iter vezes
 X=X-f(X)/f’(X)
 Resultado=X

26. Newton-Raphson e Secante
 Os dois métodos de secante e Newton-
Raphson são próximos. O método da secante
é o método de Newton-Raphson aonde a
derivada no ponto inicial é substituída pela
diferencia finita. A vantagem da secante é
que não é necessário conhecer a função
derivada.

27. Convergência
 A convergência desses métodos é em geral
mais rápida que no caso da bisseção. O
método da bisseção usa sempre o mesmo
algoritmo para qualquer função enquanto os
outros métodos usam o comportamento da
curva (diferencia finita ou derivada) para se
aproximar da raiz.

28. Convergência
 Se Newton-Raphson e
Secante podem ser
mais eficiente, elas
podem ser também
com dificuldade de
convergência se a
função tem variação
do sinal da derivada
próxima da raiz
procurada.

29. Convergência
 Vários critérios podem ser usados para decidir de
para a aplicação do algoritmo:
 um número dado de iterações,
 quando a diferencia entre dois passo de uma iteração é
menos que um erro |xi+1-xi|< ε,
 quando o valor da função em xi é perto de 0 |f(xi)|<ε,
 quando os dois últimos critérios não para o algoritmo, ele
pode ser parado porque considerado como não
convergente.