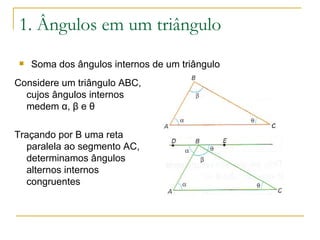
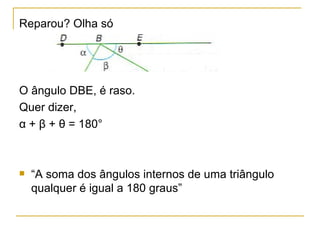
1) A soma dos ângulos internos de um triângulo é igual a 180 graus.
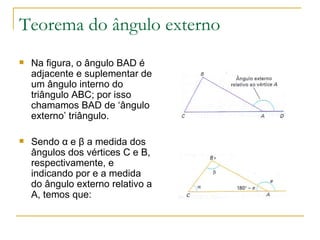
2) A medida do ângulo externo de um triângulo é igual à soma dos ângulos internos dos outros dois vértices.
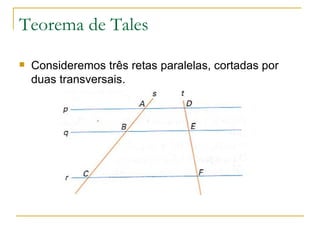
3) O teorema de Tales estabelece que a razão entre segmentos de uma transversal é igual à razão entre os segmentos correspondentes na outra transversal.