O documento explora conceitos de sistemas, caos e complexidade, definindo sistemas como conjuntos de elementos interdependentes que podem ser abertos ou fechados e simples ou complexos. Destaca a teoria do caos, que descreve sistemas complexos dinâmicos que são imprevisíveis e sensíveis a condições iniciais, além de abordar suas aplicações na medicina e na compreensão das interações biológicas. Por fim, enfatiza a importância de entender essas dinâmicas para a adaptação e eficácia das organizações e dos seres vivos.

1. SISTEMAS, CAOS E
COMPLEXIDADE
Engo. E Prof. FERNANDO ALCOFORADO

2. CONCEITO DE SISTEMA
• Sistema é um conjunto de elementos
interdependentes e interagentes no sentido de
alcançar um objetivo ou finalidade.
• Segundo Bertalanffy, é um conjunto de unidades
reciprocamente relacionadas, de onde decorrem
dois conceitos: o de objetivo e o de totalidade.
Esses dois conceitos retratam duas características
básicas de um sistema.

3. TIPOS DE SISTEMAS
Existem diferentes tipos de sistemas, que podem ser
diferenciados quanto à sua constituição e quanto à sua
natureza.
Constituição
Sistemas Físicos (ser vivo, natureza, máquinas, objetos, equipamentos)
Sistemas Abstratos (ideias, conceitos, hipóteses, planos e filosofias)
Natureza
Sistemas Fechados (não troca energia, informações, matéria, com o
ambiente, nem o influência)
Sistemas Abertos (interage com o ambiente, troca energia, informações,
matéria, sofrendo mudanças, ajustando-se e adaptando-se continuamente,
para sobreviver ás condições do meio)
Ex.: indivíduo, grupo, organização e a sociedade

4. SISTEMAS SIMPLES, COMPLEXO,
ESTÁVEIS E DINÂMICOS
• Sistema simples é aquele que possui poucos
componentes e a relação entre os componentes é
direta.
• Sistema complexo possui muitos elementos que são
altamente relacionados e interconectados. Exemplos
de sistemas complexos incluem sistemas sociais (redes
sociais), biológicos (colônias de animais) e físicos
(clima).
• Sistema estável é aquele em que mudanças no
ambiente resultam em pouca ou nenhuma mudança
no sistema.
• Sistema dinâmico é o que sofre mudanças rápidas e
constantes devido à mudança de seu ambiente.

5. SISTEMAS COMPLEXOS
1. dinâmico, adaptativo e não
linear
2. caótico, imprevisível e
sensível às condições iniciais
3. aberto, auto-organizável e
sensível ao feedback ou
realimentação

6. SISTEMA COMPLEXO, DINÂMICO,
ADAPTATIVO E NÃO LINEAR
•
• O sistema complexo, dinâmico, adaptativo e não linear é
todo sistema que envolve elementos ou agentes, não
necessariamente em grande número, que interagem
entre si, formando uma ou mais estruturas que se
originam das interações entre tais agentes.
• Um aspecto relevante é que este tipo de sistema está
constantemente revisando e reorganizando seus blocos
construtores à medida que ele ganha experiência.
• Gerações sucessivas de organismos modificarão e
reorganizarão seus tecidos através do processo de
evolução.
• O cérebro, por exemplo, continuará a se fortificar ou
enfraquecer suas conexões entre seus neurônios na
medida em que um indivíduo estabelece uma troca com
o meio ambiente.

7. SISTEMA COMPLEXO CAÓTICO, IMPREVISÍVEL E
SENSÍVEL ÀS CONDIÇÕES INICIAIS
• O sistema complexo caótico, imprevisível e
sensível às condições iniciais se caracteriza
pela incapacidade de prever seus estágios
futuros porque uma pequena mudança nas
condições iniciais do sistema pode ocasionar
grandes implicações em seu comportamento
futuro.
• Pode-se tomar como exemplo a meteorologia
que é um sistema complexo em estado
permanentemente caótico e o sistema
capitalista mundial que é um sistema sujeito a
crises cíclicas permanentes na sua evolução.

8. SISTEMA COMPLEXO ABERTO, AUTO-ORGANIZÁVEL
E SENSÍVEL AO FEEDBACK
• O sistema complexo aberto, auto-organizável e sensível ao
feedback troca insumo ou energia com o ambiente e é
suscetível às mudanças resultantes de feedback,
adaptando-se ao novo ambiente e aprendendo por meio
de sua experiência.
• Quanto mais complexo um sistema (seres vivos e sistema
econômico, por exemplo) maior é o número de feedbacks
que apresenta desenvolvendo assim, propriedades
completamente novas denominadas de emergência.
• Outra característica fundamental é a capacidade que o
sistema tem de promover a seleção natural e auto-organização.

9. TEORIA DOS SISTEMAS
Os sistemas são definidos em função dos
seguintes conceitos:
• Entrada (input)
• Processamento
• Saída (output)
• Retroação (feedback)
• Ambiente

10. TEORIA DOS SISTEMAS
Definição de alguns parâmetros dos sistemas:
Entrada (input); Processamento; Saída (output);
Retroação (feedback); Ambiente
Entrada Saída
Ambiente Processamento Ambiente
Retroação

11. COMPONENTES E CARACTERÍSTICAS DE UM SISTEMA
Ambiente
Sistema
Entradas Saídas
Subsistema Subsistema
Transformação
Atividades operacionais
Atividades gerenciais
Tecnologia
Métodos operacionais
Subsistema Subsistema
Feedback
Ambiente
homeostase
Entropia
Matéria – prima
Talentos humanos
Capital
Equipamentos
informação
Produtos
Serviços
Resultados financeiros
Informação
Satisfação do colaborador

12. HOMEOSTASE
• É a capacidade do organismo de
apresentar uma situação físico-química
característica e constante, dentro de
determinados limites, mesmo diante de
alterações impostas pelo meio ambiente.
• Para conservar constante as condições da
vida, o organismo mobiliza os mais
diversos sistemas, como o sistema
nervoso central, o endócrino, o excretor,
o circulatório, o respiratório etc.

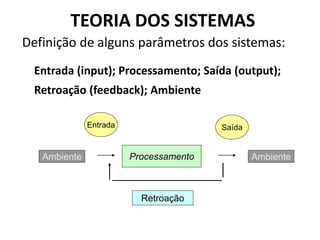
13. ENTROPIA
• Grandeza termodinâmica que expressa o grau de
desordem de um sistema reversível
• Mede a energia do sistema que não pode se
transformar em trabalho e se dissipa
• Quanto mais desordenada a energia, maior a
entropia e menor a quantidade de trabalho
obtida [Símbolo: S]
• Na teoria da informação, a entropia expressa o
grau de desordem ou de imprevisibilidade da
informação
• Quanto menos informação no sistema, maior a
entropia
• Medida da desordem de um sistema

14. TEORIA DOS SISTEMAS
• A perspectiva Sistêmica mostra a extrema importância das
constantes interações entre a organização e o ambiente.
• A organização passa a ser um sistema dinâmico que se
adapta de acordo com as situações e pressões do ambiente.
• Assegura-se a sobrevivência e a eficácia de uma
organização, na sua capacidade de adaptação ao meio em
que está inserida.
• Aqui, a organização, é primeiramente pensada na sua
função global para depois ser analisada nos seus
componentes.

15. MODELOS DETERMINÍSTICO E
ESTOCÁSTICO
• Modelo Determinístico: modelos de simulação
que não contém nenhuma variável aleatória são
classificados como determinísticos, ou seja, para
um conjunto conhecido de dados de entrada
teremos um único conjunto de resultados de
saída.
• Modelo Estocástico: possui uma ou mais
variáveis aleatórias como entrada, que levam a
saídas aleatórias. É utilizada quando pelo menos
uma das características operacionais é dada por
uma função de probabilidade.

16. DETERMINISMO E CAOS DETERMINÍSTICO
Determinismo
• O determinismo é uma doutrina filosófica que propõe que todo evento tem
uma causa e que, ocorrendo esta causa, o evento acontece invariavelmente.
• Esta concepção nega o elemento de acaso, opondo-se, de certa maneira, ao
livre-arbítrio, ou seja, que no que se refere aos desejos humanos, eventos
precedentes não determinam os subsequentes.
• O determinismo foi formulado como princípio universal da Natureza pelo
astrônomo e físico Pierre Simon de Laplace (1749-1827).
Caos Determinístico
• O caos é um comportamento imprevisível e aparentemente aleatório que
acontece em um sistema que deveria ser governado por leis naturais bem
definidas.
• Sistemas como estes, regidos por leis físicas bem definidas e cujo
comportamento poderia ser, em princípio, previsto, são chamados sistemas
determinísticos.
• O caos que eventualmente aparece nestes sistemas é chamado de caos
determinístico.

17. AS MANIFESTAÇÕES DO CAOS DETERMINÍSTICO
O caos determinístico pode ser encontrado em inúmeros fenômenos do cotidiano. Pode ser
encontrado, por exemplo, em:
• bandeiras drapejando ao vento
• torneiras gotejando
• variações climáticas
• aviões em voo
• petróleo em dutos subterrâneos
• populações em ecossistemas
• epidemias
• ritmos cardíacos
• grande mancha vermelha de Júpiter
• ciclos econômicos e preços de mercadorias
• ruídos em linhas de transmissão
• cheias de rios
• crescimento de cristais
• terremotos
• fumaça de cigarro em ascensão

18. TURBULÊNCIAS
• A turbulência é um dos fenômenos mais claramente associados ao
caos. Ocorre quando o movimento das partículas de um fluido (um
líquido ou um gás) acontece de maneira desordenada, em
trajetórias irregulares.
• Existem circunstâncias em que as turbulências são desejáveis,
como na otimização da mistura entre o ar e o combustível no
interior da câmara de combustão do motor de um avião a jato.
• São indesejáveis, entretanto, em muitas outras circunstâncias,
dissipando preciosas quantidades de energia, ou criando situações
perigosas, como sobre asas de aviões, no interior de oleodutos ou
no fluxo sanguíneo através de válvulas cardíacas artificiais.
• Uma maneira de provocar turbulência é fazer um fluido mover-se
ao redor de um obstáculo, por exemplo um rio ao redor de uma
árvore.
• A baixas velocidades, surge somente um rastro sutil atrás do
objeto.

19. SISTEMAS DINÂMICOS

20. ORDEM E CAOS

21. EVOLUÇÃO DA NATUREZA

22. NÍVEL DE ORGANIZAÇÃO DA
SOCIEDADE AO LONGO DA HISTÓRIA

23. CAOS NA ECONOMIA MUNDIAL

24. BIFURCAÇÕES E CAOS
Robert May, um físico que virou biólogo no início da década de 1970 enquanto trabalhava no
Instituto de Estudos Avançados em Princeton, nos Estados Unidos, estudou detalhadamente uma
função matemática utilizada para descrever a população de certas espécies ao longo dos anos:
x[n+1] = b * x[n] * ( 1 - x[n])
Nesta função, x[n] é a população num determinado ano, digamos, enquanto x[n+1] é a
população do ano seguinte. A letra b representa um número de 1 a 4 relacionado às condições
ambientais que participam do controle populacional. Por conveniência, os valores de x estão
sempre entre 0 e 1 (para populações realistas basta multiplicá-lo pelo valor máximo da
população (10.000, 50.000 ou 1.000.000, por exemplo).
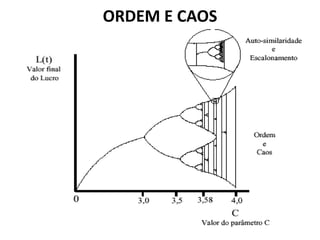
Quando o parâmetro b na equação do modelo matemático para a população atinge o valor 3 (b =
3) acontece uma surpresa. Depois de algumas interações, o valor de x fica alternando entre 0,59
e 0,73.
Esta alternância entre dois valores continua até b = 3,46, quando passa a oscilar entre 4 valores.
Neste ponto há uma nova bifurcação. Aumentando um pouco mais o valor de b, passamos a ter 8
valores, depois 16 etc., até que a partir de b = 3,569 eles não mais se repetem (exceto em
algumas "janelas"). É o caos.
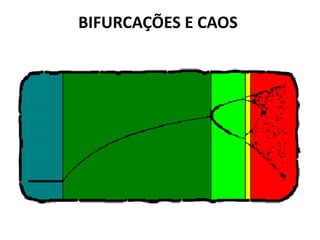
O gráfico a seguir ilustra o processo. No eixo horizontal, crescendo para a direita, está o valor de
b. No eixo vertical, crescendo para cima, os valores para os quais x converge após várias
interações.

25. BIFURCAÇÕES E CAOS

26. ATRATORES E FRACTAIS
• Um atrator é o conjunto de pontos no espaço de
fase para o qual um sistema tende a ir à medida
que evolui.
• O atrator pode ser um único ponto, uma curva
fechada (ciclo limite) que descreve um sistema
de comportamento periódico, ou
Um fractal (também chamado
de atrator estranho), quando o sistema
apresenta caos.
• Em sistemas caóticos o movimento nunca se
repete, apesar de muitas vezes ter que ocorrer
dentro de certos limites. Assim, somente uma
figura infinitamente complexa - um fractal - pode
dar conta de representar esta trajetória que
nunca se repete no espaço de fase.
•

27. ATRATORES ESTRANHOS
• Quando um sistema é complexo, não linear,
aberto com insumo constante, o número de
componentes interativos e a quantidade de
energia inserida no sistema causam o
aparecimento de fractais ou “atratores
estranhos”, os quais passam a conduzir o sistema.
• Um atrator estranho pode ser definido como o
conjunto de comportamentos característicos para
o qual evoluiu um sistema dinâmico
independentemente do ponto de partida.
• Um atrator é estranho devido ao elevado grau de
incerteza dos resultados do sistema.

28. TEORIA DO CAOS
•A Teoria do Caos se relaciona ao estudo
do comportamento dos Sistemas
Complexos.
•A Teoria do Caos explica o
funcionamento de sistemas complexos e
dinâmicos.
•Nesses sistemas, inúmeros elementos
estão em interação de forma
imprevisível e aleatória.

29. SISTEMAS COMPLEXOS
• Sistemas Complexos são sistemas não lineares
caracterizados por propriedades coletivas
emergentes associadas ao sistema como um
todo. Além disso, esses sistemas têm geralmente
a característica de serem dinâmicos.
• Mudança e Tempo, são os dois aspectos
fundamentais do Caos. O Caos se refere
principalmente a como algo evolui ao longo do
tempo.
• Espaço ou Distância substituem o Tempo em
algumas situações, podendo então distinguir
entre “Caos Temporal” e “Caos Espacial”.

30. SISTEMAS DINÂMICOS
• Considera-se que nos sistemas dinâmicos haja
apenas uma quantidade desprezível de
randomicidade e, assim, o comportamento
desses sistemas é considerado determinístico
(existe sempre apenas um único evento futuro
imediato, o qual fica determinado pelo evento
que o precede).
• Além disso, uma das características fundamentais
dos sistemas dinâmicos é sua sensível
dependência das condições iniciais pelo qual,
mínimas diferenças no início de um processo
qualquer, podem levar a situações
completamente opostas ao longo do tempo.

31. MEDICINA E SISTEMAS COMPLEXOS
• A Medicina como um todo, por lidar com a interação
de grande quantidade de fatores, deveria ser focalizada
sob o aspecto da não linearidade, a qual seria uma de
suas principais características.
• As doenças ou os mecanismos fisiopatológicos em
geral, comportam-se como parte de um Sistema
Complexo Dinâmico Não Linear Determinístico sendo
comandados pela Teoria do Caos.
• Todo objeto biológico, mas especialmente um ser
humano, é o nexo de um grande número de causas
fracamente atuantes.
• Nenhuma, nem mesmo poucas dessas causas
determinam a vida dos organismos.
• É essa estrutura de interação de múltiplos percursos
causais que torna livres as criaturas vivas.

32. MEDICINA E SISTEMAS COMPLEXOS
• A maioria dos sistemas existentes na natureza é do tipo
dinâmico (muda ao longo do tempo), com elevado
componente determinístico, sendo não linear e com
dependência sensível das condições iniciais. Isto é Caos!
• O organismo humano, indubitavelmente é um sistema
com todas as características acima mencionadas.
• Até o momento, porém, os que se ocupam da Medicina
têm-se concentrado preferencialmente em uma
abordagem linear na qual os fenômenos quase sempre
são tratados de forma estática (análise em um
determinado ponto, transversal) e os efeitos são
considerados diretamente proporcionais à causa, sendo
pouco valorizado o comportamento dinâmico e não
linear.

33. MEDICINA E SISTEMAS COMPLEXOS
• Nas situações clínicas, encontramos uma
assombrosa variabilidade nas condições finais
com sensível dependência da condição inicial.
• Assim, pequenas disfunções em órgãos isolados
levam paulatinamente a certos graus de
disfunção à distância que progressivamente vão
se associando e, de acordo com variáveis
dependentes ou não de cada indivíduo, culminam
às vezes em situações catastróficas como a
morte.
• Isto explicaria porque os clínicos estão cada vez
mais cientes da crescente onda de interesse a
respeito da dinâmica não linear.

34. MEDICINA E SISTEMAS COMPLEXOS
• O ser humano é constituído de sete
octilhões de átomos distribuídos em cerca
de 10 trilhões de células.
• Essas células constituem os tecidos dos
vários órgãos, os quais têm diferentes
funções e interagem continuamente ao
longo da vida de cada indivíduo.
• Sabe-se que o comportamento caótico
determinístico pode ocorrer já em sistemas
com pelo menos três graus de liberdade.

35. MEDICINA E SISTEMAS COMPLEXOS
• No organismo humano já foram detectados
vários componentes com padrão caótico tais
como a distribuição anatômica das árvores
arterial, venosa, brônquica além de variáveis
fisiológicas como, por exemplo, o intervalo entre
os batimentos cardíacos, a pressão arterial, o
fluxo sanguíneo, a respiração e a marcha, entre
outros.
• Infere-se daí que o ser humano deve comportar-se
como um sistema dinâmico complexo não
linear.
• Assim sendo, estaria sob este aspecto,
comandado pelas leis do Caos.

36. LEIS DO CAOS
• Em “As leis do Caos”, Ilya Prigogine,
comentando sobre pontos de bifurcação
em reações químicas, afirma que “eles
demonstram que até mesmo em nível
macroscópico a nossa predição do futuro
mistura determinismo e probabilidade.
No ponto de bifurcação, a predição tem
caráter probabilístico, ao passo que
entre os pontos de bifurcação, podemos
falar de leis deterministas”.

37. VARIÁVEIS FISIOLÓGICAS E A TEORIA
DO CAOS

38. VARIÁVEIS FISIOLÓGICAS E A TEORIA
DO CAOS

39. VARIÁVEIS FISIOLÓGICAS E A TEORIA
DO CAOS