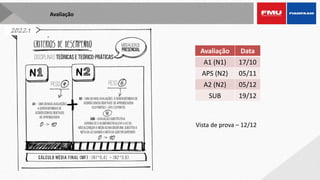
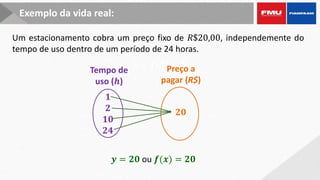
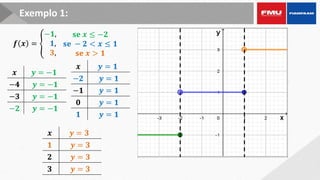
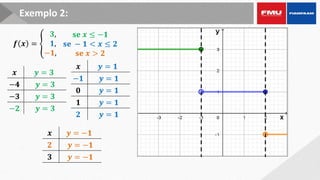
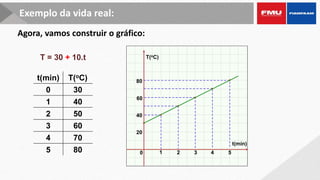
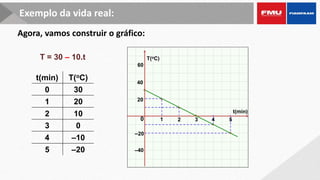
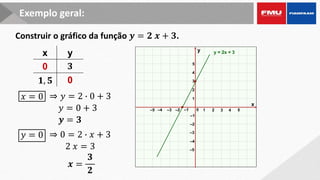
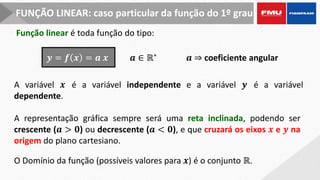
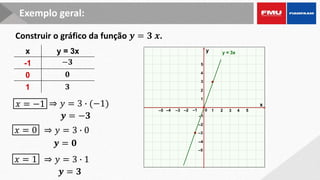
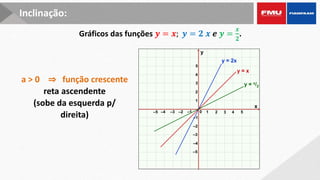
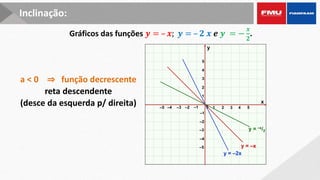
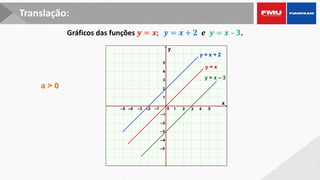
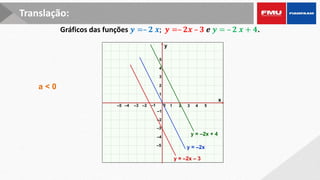
Este documento apresenta os objetivos e conteúdos de um curso de Cálculo Aplicado com uma variável. Os tópicos incluem identificar gráficos de funções elementares, analisar situações envolvendo funções trigonométricas, reconhecer propriedades de limites e derivadas, e calcular integrais utilizando diversos métodos.



![Bibliografia básica
DEMANA, Franklin D. [et al.]. Pré-Cálculo. Pearson 400 ISBN
9788588639379.
FLEMMIN, Diva Marília; Gonçalves, Mirian Buss. Cálculo A:
funções, limites, derivação e integração - 6ª edição ver.e
ampl. Pearson 458 ISBN 9788576051152.
STEWART, James. Cálculo, v.1. 3. São Paulo Cengage
Learning 2013 1 recurso online ISBN 9788522114610.](https://image.slidesharecdn.com/powerpointpresentation-netooliveira-221120235731-aadb86af/85/PowerPoint-Presentation-Neto-Oliveira-pdf-4-320.jpg)