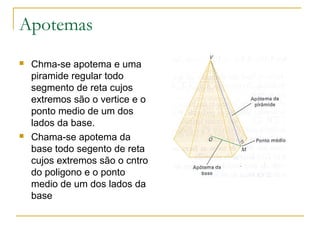
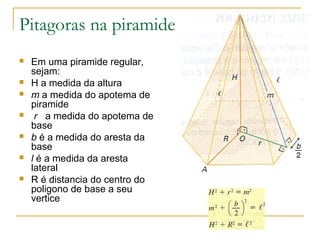
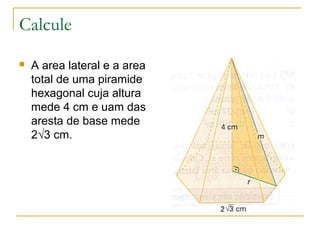
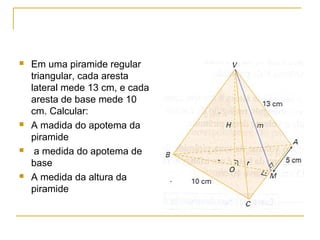
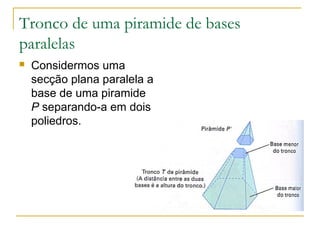
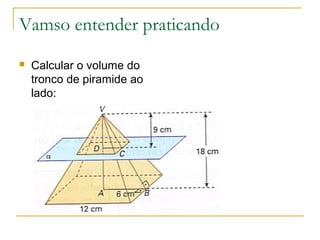
O documento descreve as pirâmides geométricas, definindo seus elementos como vértice, base, faces laterais e altura. Classifica as pirâmides em retas e regulares de acordo com a base. Explica como calcular a área lateral, total e volume de pirâmides usando o Teorema de Pitágoras e fórmulas como o volume ser 1/3 da área da base vezes a altura. Por fim, introduz o conceito de tronco de pirâmide.

1. Pirâmides
 Considere uma região poligonal convexa e
um ponto V que não pertence ao plano da
região poligonal.
 Considere também todos os segmentos de
reta com um extremo em um dos vértices da
região poligonal e outro extremo no ponto V
 Junta tudo e tem uma Pirâmide

2. Elementos de pirâmide
 O ponto V é chamado de
vértice da pirâmide
 A região poligonal é
chamada de base
 Os vértices da região
poligonal são os vértices da
base
 E o polígono é o polígono
de base
 As demais faces, que não a
base, são chamadas de
faces laterais
 As arestas não
pertencentes a base, são
arestas laterais
 A distancia entre o vértice V
e o plano da base é a altura
da pirâmide
 A soma das áreas das
faces laterais é a área
lateral
 E a soma da área da base
com a área lateral é a área
total

3. Classificação
 A Pirâmide é denominada de acordo com o
numero de arestas de base
 pirâmide reta. É aquela em que a projeção
do vértice sobre o plano de base é o centro
do polígono da base
 Pirâmide regular, é a pirâmide reta e seu
polígono de base é regular.

4. Apotemas
 Chma-se apotema e uma
piramide regular todo
segmento de reta cujos
extremos são o vertice e o
ponto medio de um dos
lados da base.
 Chama-se apotema da
base todo segento de reta
cujos extremos são o cntro
do poligono e o ponto
medio de um dos lados da
base

5. Pitagoras na piramide
 Em uma piramide regular,
sejam:
 H a medida da altura
 m a medida do apotema de
piramide
 r a medida do apotema de
base
 b é a medida do aresta da
base
 l é a medida da aresta
lateral
 R é distancia do centro do
poligono de base a seu
vertice

6. Calcule
 A area lateral e a area
total de uma piramide
hexagonal cuja altura
mede 4 cm e uam das
aresta de base mede
2√3 cm.

7.  Em uma piramide regular
triangular, cada aresta
lateral mede 13 cm, e cada
aresta de base mede 10
cm. Calcular:
 A madida do apotema da
piramide
 a medida do apotema de
base
 A medida da altura da
piramide

8. Volume
 Dessa vez, não tm como entender, então aceitem:
 Volume da piramide é igual a ⅓ do produto da area
de base pela altua da piramide.
 V = ⅓ BH

9. Tronco de uma piramide de bases
paralelas
 Considermos uma
secção plana paralela a
base de uma piramide
P separando-a em dois
poliedros.

10. Vamso entender praticando
 Calcular o volume do
tronco de piramide ao
lado:

11. Pronto
CHEEEGA!!!
Até semana que vem com ‘Corpos redondos’