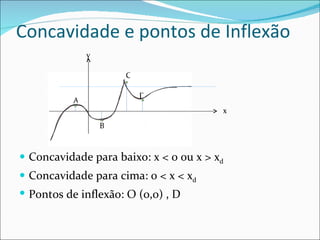
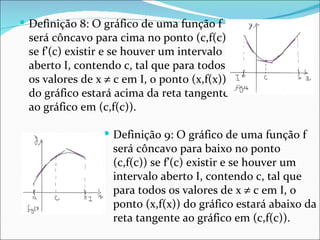
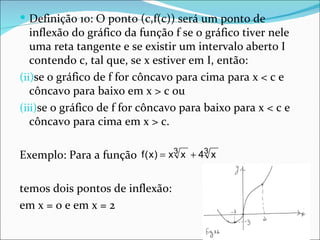
1) A professora apresenta conceitos geométricos e analíticos relacionados à derivada e seus pontos críticos. 2) São definidos e explicados os Teoremas do Valor Médio, de Rolle e critérios para identificar intervalos de crescimento de funções. 3) Concavidade, pontos de inflexão e seus critérios de identificação com base na segunda derivada são explicados.

1. Profª Débora Bastos

2. Recapitulação Interpretação geométrica da derivada: f’(c) = tg  , desde que  seja o ângulo da reta tangente à f em x=c. P (c,f(c)) é crítico se f’(c) = 0 ou se f’(c) não existe. Se f é continua e derivável em [a,b] contendo c, então existe máximo absoluto e mínimo absoluto em [a,b] entre os pontos críticos encontrados e os extremos do intervalo.

3. Teoremas importantes. Teorema 3 (Teorema do valor médio): Seja f uma função tal que: Seja contínua num intervalo fechado [a,b]; Seja derivável no intervalo (a,b). Então existirá um número c no intervalo aberto (a,b) tal que: Interpretação geométrica P(a,f(a)), Q(b,f(b))  s R(c,f(c))  t Existe c para que a reta t nesse ponto Tem a mesma inclinação da reta s.

4. Exemplo Verifique o TVM para f(x) = x -1 , x  [2,3] f é contínua em lR*  contínua em [2,3] f é derivável em lR*  contínua em [2,3] f´(x)=  x -2 f(2) = ½ f(3) = 1/3

5. Teorema 4: (Teorema de Rolle) Seja f uma função tal que: Contínua em [a,b] Derivável em (a,b) f(a)=f(b)=0 Então existe um número c em (a,b), tal que f’(c) = 0. Caso particular do TVM: Existe c tal que O TR afirma que f que satisfaz as condições necessárias possui ao menos um ponto extremo entre as raízes da função (x / f(x) = 0).

6. O TR garante a existência e não a unicidade. Exemplos: Importante satisfazer as condições do teorema: O gráfico ao lado não é Contínua e não possui ponto de máximo.

7. Funções Crescentes e Decrescentes. Definição 6: Dizemos que uma função f, definida num intervalo I, é crescente neste intervalo se para quaisquer x 1 , x 2  I, x 1 < x 2 , temos f(x 1 ) < f(x 2 ) Definição 7: Dizemos que uma função f, definida num intervalo I, é crescente neste intervalo se para quaisquer x 1 , x 2  I, x 1 < x 2 , temos f(x 1 ) > f(x 2 )

8. Observação Assim como os pontos extremos, reconhecer os intervalos em que uma função é crescente ou decrescente é fácil, desde que o gráfico esteja bem feito. Nosso trabalho é através apenas da lei da função descobrir quando isso acontece com fim de esboçar o gráfico dessa função. Servirá também para diferenciar um ponto de máximo de um ponto de mínimo, ou se não há pontos extremos.

9. Pontos extremos e crescimento Não importa a característica do gráfico se um ponto P(c,f(c)) é de máximo local, este um intervalo (a,b) em que f é crescente para a < x < c e f é decrescente para c < x <b.

10. De forma análoga, se o ponto P(c,f(c)) é ponto de mínimo local existe intervalo aberto (a,b) em que f é decrescente para a < x < c e é crescente para c < x < b.

11. Critério para determinar o tipo de crescimento. * Função crescente #Função Decrescente *Se f é crescente em (a,b) as retas tangentes à função em (a,b) formam um ângulo agudo com o eixo ox (0 <  <90 0 ) #Se f é decrescente em (a,b) as retas tangentes à função em (a,b) formam um ângulo obtuso com o eixo ox (90 0 <  <180 0 )

12. Para 0 <  <90 0 tem-se tg  > 0 (positiva) Para 90 0 <  <180 0 tem-se tg  < 0 (negativa) Pela interpretação geométrica da derivada temos: f´(x) > 0 para x  (a,b) f´(x) < 0 para x  (a,b)

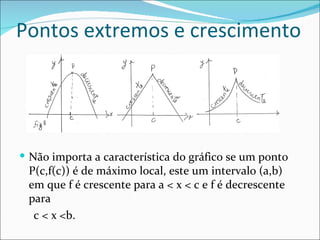
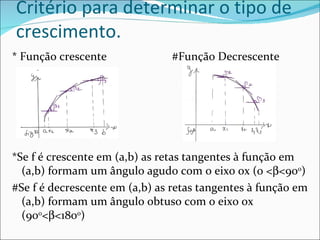
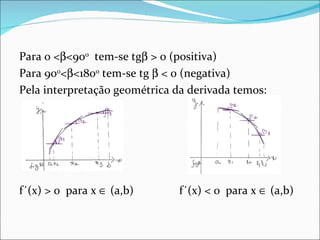
13. Teorema 5: Seja f uma função contínua no intervalo fechado [a,b] derivável no intervalo (a,b). Se f’(x) > 0 para todo x  (a,b), então f é crescente em [a,b] Se f’(x) < 0 para todo x  (a,b), então f é decrescente em [a,b] Obs.: O TVM faz parte da demonstração desse teorema. Exemplo: Dada f(x) = x 3 – 6x 2 + 9x + 1, ache os extremos relativos de f, determine os intervalos em que f é crescente ou decrescente. Com essas informações faça o esboço do gráfico.

14. Exemplo Obs.: A derivada primeira de f tanto determina os pontos críticos quanto influi no estudo do crescimento. Solução: A função f é polinomial, ou seja, contínua e derivável em todo seu domínio. f´(x) = 3x 2 – 12x + 9 Pontos criticos x = 1 e x =3 P(1,5) é de máximo e Q(3,1) é de mínimo

15. Exemplo: Faça o mesmo para: f é contínua e derivável em lR f‘(x) não é derivável em x = 0. f’(x) = 0  x = - 1 Estudo do sinal da derivada P(-1, -3) é de mínimo local Q(0,0) não é extremo

16. Concavidade e pontos de Inflexão Concavidade para baixo: x < 0 ou x > x d Concavidade para cima: 0 < x < x d Pontos de inflexão: O (0,0) , D A B C D x y

17. Definição 8: O gráfico de uma função f será côncavo para cima no ponto (c,f(c)) se f’(c) existir e se houver um intervalo aberto I, contendo c, tal que para todos os valores de x  c em I, o ponto (x,f(x)) do gráfico estará acima da reta tangente ao gráfico em (c,f(c)). Definição 9: O gráfico de uma função f será côncavo para baixo no ponto (c,f(c)) se f’(c) existir e se houver um intervalo aberto I, contendo c, tal que para todos os valores de x  c em I, o ponto (x,f(x)) do gráfico estará abaixo da reta tangente ao gráfico em (c,f(c)).

18. Interpretação Geométrica f’(c) representa o valor da inclinação tg  da reta tangente à f em x = c. f é côncava para cima ângulo obtuso  ângulo agudos tg  < 0  tg  > 0 valores crescentes  f’(x) é crescente quando o gráfico é côncavo para cima.

19. f côncavo para baixo ângulo obtuso  ângulo agudos tg  > 0  tg  < 0 valores decrescentes  f’(x) é decrescente quando o gráfico é côncavo para cima. Devemos investigar o sinal de f’(x) onde é crescente e decrescente, mas isso é feito derivando f’(x), ou seja, o que determinará a concavidade é f’’(x).

20. Teorema 6: Seja f uma função diferenciável em algum intervalo aberto contendo c. Então: Se f’’(c) > 0 , o gráfico de f é côncavo para cima em (c,f(c)). Se f’’(c) < 0 , o gráfico de f é côncavo para baixo em (c,f(c)). Exemplo: Determine os intervalos do domínio em que a função é côncava para cima ou côncava para baixo.

21. Se um ponto (c,f(c)) é de máximo relativo ele está localizado num intervalo onde o gráfico da função é côncavo para baixo, portanto f’’(c) < 0. Já se um ponto (c,f(c)) é de mínimo relativo ele está localizado num intervalo onde o gráfico da função é côncavo para cima, portanto f’’(c) > 0. (Chamamos de teste da derivada segunda) Exemplo: Determine os pontos extremos da função f(x) = x 3 – 6x 2 + 9x + 1 f ’(x) = 3x 2 – 12x + 9 extremos x = 1 ou x = 3 f” (x) = 6x – 12 f” (1)<0  x = 1 é ponto de máximo local f” (3)>0  x = 3 é ponto de mínimo local

22. Definição 10: O ponto (c,f(c)) será um ponto de inflexão do gráfico da função f se o gráfico tiver nele uma reta tangente e se existir um intervalo aberto I contendo c, tal que, se x estiver em I, então: se o gráfico de f for côncavo para cima para x < c e côncavo para baixo em x > c ou se o gráfico de f for côncavo para baixo para x < c e côncavo para cima em x > c. Exemplo: Para a função temos dois pontos de inflexão: em x = 0 e em x = 2

23. Teorema 7: Se a função f for derivável em algum intervalo contendo c e se (c,f(c)) for um ponto de inflexão do gráfico de f, então se f’’(c) existe, f’’(c)=0. obs.: A recíproca não é verdadeira, ou seja, se f’’(c) = 0, não quer dizer que (c,f(c)) é um ponto de inflexão. Exemplo: f(x) = x 4 f ’(x) = 4x 3 f ”(x) = 12x 2 f ”(x) = 0  x = 0, mas x = 0 é um ponto de mínimo local.