Baixado 12 vezes
Carregado porosneider acevedo naranjo
Isomorfo de un grafo
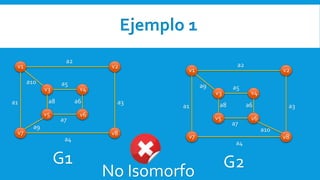
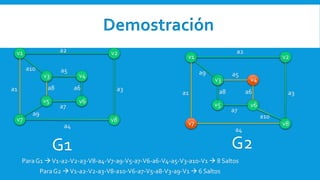
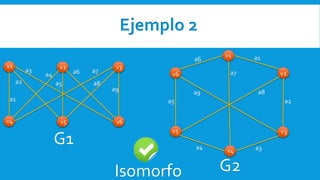
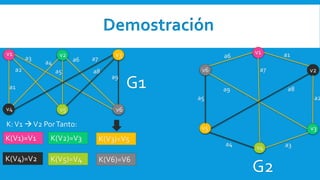
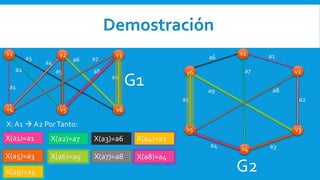
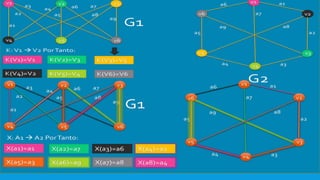
Dois grafos são isomorfos se eles possuem a mesma estrutura, diferindo apenas na representação geométrica ou rotulação de vértices e arestas. Dois grafos G1 e G2 são isomorfos se existirem funções K e X tal que K mapeia vértices de G1 para vértices de G2 de forma correspondente e X mapeia arestas de G1 para arestas de G2.
Isomorfo de un grafo
- 1.
- 2. ¿Cuando un Grafoes Isomorfo? Un grafo es isomorfo cuando se presenta el caso en que dos grafos poseen la misma estructura y difieren solamente en la forma en que han sido representados geométricamente, o en la forma, como han sido rotulados sus vértices y aristas G1 = (V1, A1, Fg1) y G2 = (V2, A2, Fg2) Existen funciones K y X K:V1 V2 y X: A1 A2 Un Grafo Isomorfo se denota como:G1 = G2
- 3. Ejemplo 1 v1 v2 v3v4 v5 v6 v7 v8 a5 a2 a3 a4 a1 a6 a7 a8 a9 a10 G1 v1 v2 v3 v4 v5 v6 v7 v8 a5 a2 a3 a4 a1 a6 a7 a8 a9 a10 G2 No Isomorfo
- 4. v8 v1 v3 v6 v8 v2 Demostración v1 v4 v5 v7 a5 a2 a3 a4 a1 a6 a7 a8 a9 a10 G1 v2 v3 v4 v5v6 v7 a5 a2 a3 a4 a1 a6 a7 a8 a9 a10 G2 Para G1 V1-a2-V2-a3-V8-a4-V7-a9-V5-a7-V6-a6-V4-a5-V3-a10-V1 8 Saltos Para G2 V1-a2-V2-a3-V8-a10-V6-a7-V5-a8-V3-a9-V1 6 Saltos
- 5. Ejemplo 2 v1 a3 G1 v2 v3 v4v5 v6 a2 a1 a4 a5 a6 a7 a8 a9 v1 a3 v3 v4 v5 v6 a2 a1 a4 a5 a6 a7 a8a9 v2 G2Isomorfo
- 6. v1 a3 G1 v2 v3 v4 v5v6 a2 a1 a4 a5 a6 a7 a8 a9 v1 a3 v3 v4 v5 v6 a2 a1 a4 a5 a6 a7 a8a9 v2 G2 Demostración K:V1 V2 PorTanto: K(V1)=V1 K(V2)=V3 K(V3)=V5 K(V4)=V2 K(V5)=V4 K(V6)=V6
- 7. v1 a3 G1 v2 v3 v4 v5v6 a2 a1 a4 a5 a6 a7 a8 a9 v1 a3 v3 v4 v5 v6 a2 a1 a4 a5 a6 a7 a8a9 v2 G2 Demostración X: A1 A2 PorTanto: X(a1)=a1 X(a2)=a7 X(a3)=a6 X(a4)=a2 X(a5)=a3 X(a6)=a9 X(a7)=a8 X(a8)=a4 X(a9)=a5
- 9.