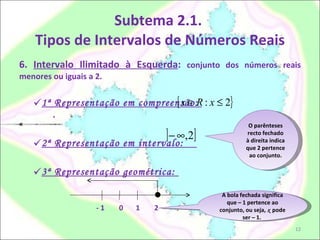
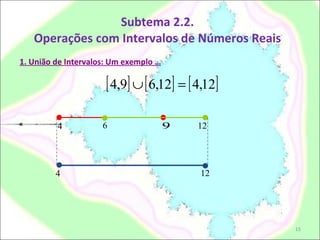
Este documento discute intervalos de números reais. Explica os seis tipos básicos de intervalos (fechado, aberto, aberto à direita/esquerda, ilimitado à direita/esquerda) e como representá-los em compreensão, intervalo e geometricamente. Também menciona operações com intervalos como união e intersecção, mas não fornece exemplos.

1. Tema 2. Intervalos de Números Reais 31 de Janeiro de 2011 Professora Filipa Guerreiro

2. Pense… Considere as seguintes afirmações: O tempo entre um período de aula e outro. O tempo entre uma badalada de um sino e outra. O espaço entre as fendas de uma grade. O espaço de tempo entre duas épocas. O espaço de tempo entre duas oscilações sonoras. A distância entre dois pontos. O que se poderia dizer quanto a estas afirmações?

3. Todas as afirmações transmitem a ideia de intervalo: intervalo de tempo, intervalo espacial… Tal como no nosso quotidiano, também na Matemática é comum o uso de intervalos. Hoje vamos estudar intervalos muito especiais: Intervalos de Números Reais . Nota: Intervalos de Números Reais são subconjuntos do conjunto dos Números Reais.

4. Quando falamos nos divisores de 12 sabemos que nos estamos a referir ao conjunto: Ou seja, a condição “ser divisor de 12” definiu o conjunto D. Quando escrevemos dizemos que o conjunto está representado em extensão – estão indicados todos os seus elementos . Mas será sempre possível escrever todos os elementos de um conjunto?

5. Consideremos a Recta Real: Como representar em extensão o conjunto dos números maiores ou iguais a – 1 e menores ou iguais a 2? É evidente que há uma infinidade de Números Reais nestas condições. Logo, não é possível representar este conjunto em extensão . - 5 - 4 - 3 - 2 - 1 0 1 2 3 4

6. Vejamos então três outras formas diferentes de representar este conjunto: 1ª: Representação em compreensão : . 2ª Representação em intervalo : . 3ª Representação geométrica : - 1 0 1 2 A bola fechada significa que – 1 e 2 pertencem ao intervalo, ou seja, x pode ser – 1 e 2. Os parênteses rectos fechados indicam intervalo fechado nos dois extremos, o que significa que – 1 e 2 pertencem ao conjunto.

7. Subtema 2.1. Tipos de Intervalos de Números Reais Intervalo fechado: conjunto de números reais maiores ou iguais a – 1 e menores ou iguais a 2. Representação em compreensão : . 2ª Representação em intervalo : . 3ª Representação geométrica : - 1 0 1 2 A bola fechada significa que – 1 e 2 pertencem ao intervalo, ou seja, x pode ser – 1 e 2. Os parênteses rectos fechados indicam intervalo fechado nos dois extremos, o que significa que – 1 e 2 pertencem ao conjunto.

8. 2. Intervalo aberto: conjunto de números reais maiores que – 1 e menores que 2. 1ª Representação em compreensão : . 2ª Representação em intervalo : . 3ª Representação geométrica : Subtema 2.1. Tipos de Intervalos de Números Reais - 1 0 1 2 A bola aberta significa que – 1 e 2 não pertencem ao intervalo, ou seja, x não pode ser – 1 e 2. Os parênteses rectos abertos indicam intervalo aberto nos dois extremos, o que significa que – 1 e 2 não pertencem ao conjunto.

9. Subtema 2.1. Tipos de Intervalos de Números Reais 3. Intervalo Aberto à Direita : conjunto dos números reais maiores ou iguais a – 1 e menores que 2. 1ª Representação em compreensão: . 2ª Representação em intervalo: . 3ª Representação geométrica: - 1 0 1 2 O parênteses recto fechado à esquerda e aberto à direita indica que – 1 pertence ao conjunto e 2 não pertence ao conjunto. A bola fechada significa que – 1 pertence ao intervalo e a bola aberta significa que 2 não pertence, ou seja, x pode ser – 1 mas não pode ser 2.

10. Subtema 2.1. Tipos de Intervalos de Números Reais 4. Intervalo Aberto à Esquerda : conjunto dos números reais maiores que – 1 e menores ou iguais a 2. 1ª Representação em compreensão: . 2ª Representação em intervalo: . 3ª Representação geométrica: - 1 0 1 2 O parênteses recto aberto à esquerda e fechado à direita indica que – 1 não pertence ao conjunto e 2 pertence ao conjunto. A bola fechada significa que 2 pertence ao intervalo e a bola aberta significa que – 1 não pertence, ou seja, x pode ser 2 mas não pode ser – 1.

11. Subtema 2.1. Tipos de Intervalos de Números Reais 5. Intervalo Ilimitado à Direita : conjunto dos números reais maiores ou iguais a – 1. 1ª Representação em compreensão: . 2ª Representação em intervalo: . 3ª Representação geométrica: - 1 0 1 2 O parênteses recto fechado à esquerda indica que – 1 pertence ao conjunto. A bola fechada significa que – 1 pertence ao conjunto, ou seja, x pode ser – 1.

12. Subtema 2.1. Tipos de Intervalos de Números Reais 6. Intervalo Ilimitado à Esquerda : conjunto dos números reais menores ou iguais a 2. 1ª Representação em compreensão: . 2ª Representação em intervalo: . 3ª Representação geométrica: - 1 0 1 2 O parênteses recto fechado à direita indica que 2 pertence ao conjunto. A bola fechada significa que – 1 pertence ao conjunto, ou seja, x pode ser – 1.

13. Subtema 2.1. Tipos de Intervalos de Números Reais Represente em compreensão, em intervalo e geometricamente os seguintes conjuntos: Conjunto dos números reais maiores que – 1; Conjunto dos números reais menores que 2.

14. Subtema 2.2. Operações com Intervalos de Números Reais 1. União de Intervalos:

15. Subtema 2.2. Operações com Intervalos de Números Reais 1. União de Intervalos: Um exemplo …

16. Subtema 2.2. Operações com Intervalos de Números Reais 2. Intersecção de Intervalos:

17. Subtema 2.2. Operações com Intervalos de Números Reais 2. Intersecção de Intervalos: Um exemplo …

18. Subtema 2.2. Operações com Intervalos de Números Reais Exercício: Dados os intervalos calcule e represente em compreensão, em intervalo e geometricamente:

19. Obrigada pela atenção!