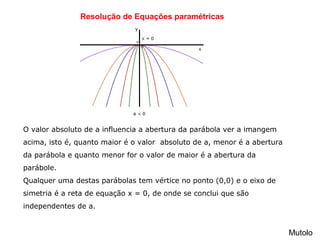
Uma função quadrática é definida como f(x) = ax2 + bx + c, onde a, b e c são coeficientes reais e a ≠ 0. O gráfico de uma função quadrática é uma parábola, cuja concavidade depende do sinal de a. Quanto maior o valor absoluto de a, menor a abertura da parábola.

1. Identificar uma Função quadrática
Função quadrática ou função do segundo grau é uma aplicação f de R R→
na forma f(x) = ax² + bx + c.
Onde: a, b e c são coeficientes e pertencem ao conjunto R e a ≠ 0.
Se a = 0 teremos f(x) = 0x2
+ bx + c correspondente a uma equação linear
do tipo f(x) = bx + c. Essa restrição é apenas para o valor de “a”, pois b e c
podem ser iguais a zero a função continuará quadrática.
Exemplos de funções quadráticas
f(x) = 8x² – 4x + 1, onde a = 8, b = – 4 e c = 1
f(x) = x² -x, onde a = 1, b = -1 e c = 0
f(x) = 3x2
- 4x + 1, onde a = 3, b = - 4 e c = 1
f(x) = x2
-1, onde a = 1, b = 0 e c = -1
f(x) = 2x2
+ 3x + 5, onde a = 2, b = 3 e c = 5
O gráfico de uma função quadrática, f(x) = ax2
+ bx + c é uma curva
chamada
parabola. Para construir o seu gráfico é necessário compor uma tabela
auxiliar de valores de x e y

2. Resolução de Equações paramétricas
Mutolo
Exemplo de famílias de gráficos que representa a função quadrática do
tipo y = ax² com valores de b e c iguais a zero.
o sinal do coeficiente a influencia o sentido da concavidade:
Quando a > 0, parábola tem uma concavidade virada para cima.
Quando a < 0, parábola tem uma concavidade virada para baixo.

3. Resolução de Equações paramétricas
Mutolo
O valor absoluto de a influencia a abertura da parábola ver a imangem
acima, isto é, quanto maior é o valor absoluto de a, menor é a abertura
da parábola e quanto menor for o valor de maior é a abertura da
parábole.
Qualquer uma destas parábolas tem vértice no ponto (0,0) e o eixo de
simetria é a reta de equação x = 0, de onde se conclui que são
independentes de a.