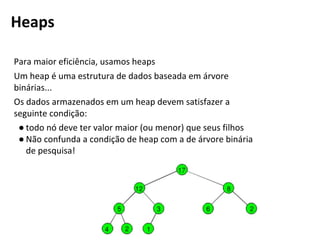
O documento discute filas de prioridade e como implementá-las de forma eficiente. Duas abordagens são descritas: uma que é eficiente para inserções e outra para remoções. Heaps são introduzidos como uma estrutura de dados que pode representar filas de prioridade de forma eficiente.

1. Heap (Python)
prof. sergio souza costa

2. Sobre mim
Sérgio Souza Costa
Professor - UFMA
Doutor em Computação Aplicada (INPE)
prof.sergio.costa@gmail.com
https://sites.google.com/site/profsergiocosta/home
https://twitter.com/profsergiocosta
http://gplus.to/sergiosouzacosta
http://www.slideshare.net/skosta/presentations?order=popular

3. Filas de prioridade
Diferentemente das filas comuns, neste caso, um elemento ao entrar na fila
tem prioridade.
O primeiro a sair não é necessariamente o primeiro a entrar

4. Filas de prioridade
Exemplos de aplicação
● Uma fila de pacientes esperando transplante de orgão.
● Em sistemas operacionais, a fila de prioridade de processos aguardando o
processador para execução.
○ Os processos mais prioritários são executados antes dos outros
Veremos algumas formas de implementar uma fila de prioridade. Algumas são
eficientes na inserção, outras na remoção.

5. Filas de prioridade
Fila de prioridade é uma estrutura de dado que mantém uma coleção de
elementos, cada um com uma prioridade associada. Valem as operações
seguintes:
● Inserir um elemento novo na fila de prioridade.
● Remover o elemento de maior prioridade da fila de prioridade.

6. Filas de prioridade
Eficiente na inserção:
● cada elemento inserido é anexado à lista
● a cada extração, percorremos a lista em busca do elemento com maior
prioridade
Se há n elementos na fila, então...
● O(1) para inserções
● O(n) para extrações

7. Filas de prioridade
Eficiente na remoção:
● a cada inserção, a fila é percorrida até o ponto de inserção, inserção
ordenada.
● a extração é sempre do primeiro elemento
Se há n elementos na fila, então...
● O(n) para inserções
● O(1) para extrações

8. Filas de prioridade
Eficiente na inserção:
Para esta codificação não precisamos modificar a função enfileira
Precisamos modificar a função dequeue (desenfileira).
○ Primeiro encontramos o maior valor, percorrendo a lista da fila.
○ Depois removemos este valor da lista (list_remove)
○ Por fim, retornamos o maior valor

9. Filas de prioridade
Eficiente na remoção:
Para esta codificação não precisamos modificar a função desenfileira.
Precisamos modificar a função enfileira.
● Neste caso, inserimos ordenado dentro da lista.

10. Para maior eficiência, usamos heaps
Um heap é uma estrutura de dados baseada em árvore
binárias...
Os dados armazenados em um heap devem satisfazer a
seguinte condição:
● todo nó deve ter valor maior (ou menor) que seus filhos
● Não confunda a condição de heap com a de árvore binária
de pesquisa!
Heaps

11. Podemos representar heaps em vetores
A idéia é linearizar a árvore por níveis
● a raíz é armazenada na primeira posição do vetor,
● o filho à esquerda da raíz na segunda posição,
● o filho à direita da raíz na terceira,
● o primeiro neto da raíz na quarta,
● etc..
Heaps - Representação

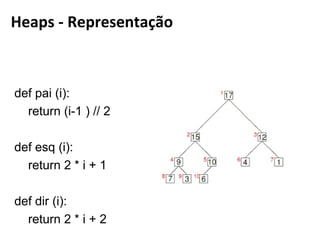
12. Heaps - Representação
class BinHeap:
def __init__(self):
self.l = []
0 1 2 3 4 5 6 7 8 9 10 11 12
17 15 12 9 10 4 1 7 3 6
0
1 2
3 4 5 6
7 8 9

13. def pai (i):
return (i-1 ) // 2
def esq (i):
return 2 * i + 1
def dir (i):
return 2 * i + 2
Heaps - Representação
0
1 2
3 4 5 6
7 8 9

14. Para inserir um novo elemento com prioridade e,
● Adiciona-se um novo elemento e no fim da lista.
Isso pode perturbar a propriedade do “heap”. Para consertar
isso:
● se e for maior que seu pai, então os dois trocam de lugar.
● essa operação é repetida até que e encontre o seu lugar
correto para o elemento e.
Heaps - Representação

15. Heaps - Inserção

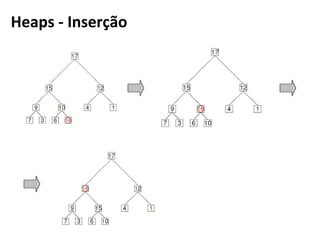
16. def insere (h, x):
# adiciona no fim da lista
h.l.append (x)
i = len (h.l) - 1
# procura novo lugar para o valor
while i > 0 and h.l[pai (i)] < x:
h.l[i] = h.l[pai(i)]
i = pai (i)
h.l[i] = x
Heaps - Inserção

17. A remoção em si é muito simples, já que o elemento de maior
prioridade está na primeira posição.
Após a remoção, entretanto, precisamos rearranjar os
elementosdo“heap”:
● Colocamos na primeira posição o elemento da última posição, e
executa a correção.
def extraiMaximo (h):
if h.l != []:
maior = h.l[0]
h.l[0] = h.l[-1]
h.l.pop()
corrigeHeap(h,0)
return maior
Heaps - Remoção

18. def corrigeHeap (h,i):
e = esq (i)
d = dir (i)
maior = i
if e < len (h.l) and h.l[e] > h.l[i]:
maior = e
if d < len (h.l) and h.l[d] > h.l[maior]:
maior = d
if maior != i:
h.l[i], h.l[maior] = h.l[maior],h.l[i]
corrigeHeap (h,maior)
Heap - Correção

19. Perceba que podemos ordenar os elementos em um heap sem
"dificuldades"...
Basta extrair os elementos um a um
O algoritmo conhecido como heapsort explora exatamente essa
idéia
Heap - Aplicada para a Ordenação

20. O problema é: como fazer com que os elementos de um vetor
desordenado passem à condição de heap?
Uma solução simples é usar o algoritmo de inserção repetidas
vezes...
● Custo: O(n log n)
Heapsort

21. def constroiHeap ( l):
i = len (l) // 2
h = BinHeap()
h.l = l[:]
while i >= 0:
corrigeHeap (h, i)
i = i -1
return h
Heapsort - Construção

22. def heapSort (l):
h = constroiHeap (l)
i = len (l) - 1
while (i >= 0):
l[i] = extraiMaximo (h)
i = i - 1
Heapsort