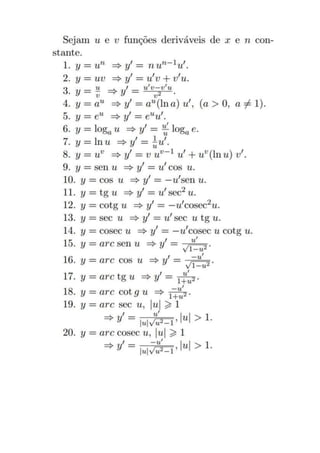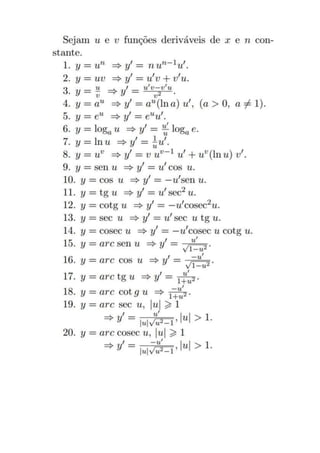
Derivadas de potências seguem a regra de que a derivada de x^a é igual a a*x^(a-1). A derivada da soma de funções é igual à soma das derivadas de cada função. A derivada da subtração de funções é igual à subtração das derivadas de cada função. A derivada do produto de funções é igual à primeira função vezes a derivada da segunda mais a derivada da primeira vezes a segunda função.

1. DERIVADAS
 Regrado “tombo” (Derivadas de potências).
Se f (x) = xa
, então f ‘ (x) = a·xa – 1.
Exemplo:
f(x)=x², então f'(x)=2.1x²– 1
f'(x)=2x¹, ou apenas f'(x)=2x
 Derivadade soma de funções.
Se y=[f(x)+g(x)], então y’=f'(x)+g'(x)
Exemplo:
y=x²+x³, então y’=2.1x¹+3.1x²
y’=2x+3x²
 Derivadade subtraçãode funções.
Se y=[f(x)-g(x)], então y’=f'(x)-g'(x)
Exemplo:
y=5x³-9x², então y’=3.5x²-2.9x¹
y’=15x²-18x
 Regrado Produto (Multiplicaçãoentre funções).
Se y=[f(x).g(x)], então y’=f'(x).g(x)+f(x).g'(x), demodo extenso,
“A derivada da primeira função, ou seja, a função f(x), vezesa segunda,
g(x), MAIS a primeira função, vezesa derivada da segunda.”
Exemplo:

2. y=x³.5 x², então y’=(3x²).(5x²)+(x³).(10x)
 Regrado Quociente (Divisãoentre funções).
Se y=f(x)/g(x), então
Exemplo:
y=x²/x³, então y’=(2x).(x³)-(x²).(3x²)/(x³)²