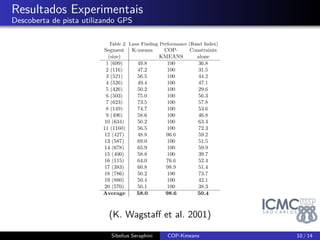
O documento discute o algoritmo COP-Kmeans para agrupamento de dados com restrições. COP-Kmeans realiza agrupamento k-means enquanto respeita restrições de nível de instância como must-link e cannot-link. O algoritmo atribui objetos a clusters sem violar restrições e atualiza centros de clusters. Resultados experimentais mostram que restrições podem melhorar agrupamento quando informativas sobre estrutura dos dados.

1. .
.
Constrained K-means Clustering with Background
Knowledge
COP-Kmeans
Sibelius Seraphini
Instituto de Ciências Matemáticas e de Computação
Universidade de São Paulo
1 de dezembro de 2014
Sibelius Seraphini COP-Kmeans 1 / 14

2. . k-Means
1. Escolhe aleatoriamente k centros para os clusters
2. Atribuir cada objeto para o cluster de centro mais próximo
3. Atualizar cada centro para a média dos objetos do cluster
correspondente
Sibelius Seraphini COP-Kmeans 2 / 14

3. .
k-Means
Perspectiva de Otimização
Variância intra-cluster
min
8< :
KΣ
k=1
LΣ
i=1
2
4(xi; ck)
NΣ
j=1
(xij xkj)2
9=
3
5
;
Sibelius Seraphini COP-Kmeans 3 / 14

4. . Como incorporar conhecimento prévio?
Agrupamento de Dados Semi-Supervisionado
Restrições
Nível de Instância
Nível de Cluster
Sibelius Seraphini COP-Kmeans 4 / 14

5. . Restrições (COP-kMeans)
Restrições em Nível de Instância
Must-Link — duas instâncias devem estar no mesmo cluster
Cannot-Link — duas instâncias não devem estar no mesmo
cluster
Restrições nunca são quebradas
Sibelius Seraphini COP-Kmeans 5 / 14

6. . COP-kMeans
1. Escolhe aleatoriamente k centros para os clusters
2. Atribuir cada objeto para o cluster de centro mais próximo
sem violar as restrições
3. Atualizar cada centro para a média dos objetos do cluster
correspondente
Sibelius Seraphini COP-Kmeans 6 / 14

7. . Tratando Restrições
Para todos as instâncias tentar atribuí-lo ao centro k mais próximo
1. Sem restrição quebrada
Atribuir a instância i ao cluster k
2. Restrição quebrada ! existe outro próximo cluster?
Retorna para 1, se sim
Falhar
Sibelius Seraphini COP-Kmeans 7 / 14

8. .
COP-kMeans
Perspectiva de Otimização
min
{ΣKk
=1
ΣLi
=1
[
(xi; ck)
ΣN j=1(xij xkj)2
]}
sujeito a
1
2
ΣL
i=1
ΣLj
=1
[
Con(i; j)
[ 1
2 Con(i; j)

9. (Ii; Ij) + 1
2
]]
= 0
Con(i; j) =
8
:
1; se xi e xj é Must-Link
1; se xi e xj é Cannot-Link
0; caso contrário

10. (Ii; Ij) =
{
1; se Ii = Ij
0; caso contrário
Sibelius Seraphini COP-Kmeans 8 / 14

11. . Resultados Experimentais
(K. Wagstaff et al. 2001)
Sibelius Seraphini COP-Kmeans 9 / 14

12. .
Resultados Experimentais
Descoberta de pista utilizando GPS
(K. Wagstaff et al. 2001)
Sibelius Seraphini COP-Kmeans 10 / 14

13. . Limitações
Sensível a ordem de atribuição
Solucionado por (Hong e Kwong 2009), usando um conjunto
de algoritmos de agrupamento
Sibelius Seraphini COP-Kmeans 11 / 14

14. . Quando restrições são vantajosas?
Mesmo número de restrições leva a diferentes desempenhos
(K. L. Wagstaff, Basu e
Davidson 2006)
Inconsistência
Média de restrições
insatisfeitas utilizando o
algoritmo sem restrições
Incoerência
Os pontos envolvidos na
restrição ML deveriam
estar perto, enquanto que
pontos envolvidos na
restrição CL deveriam
estar afastados
Sibelius Seraphini COP-Kmeans 12 / 14