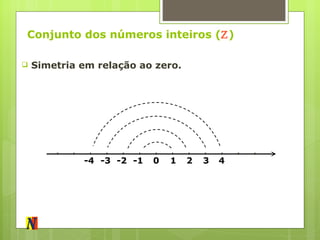
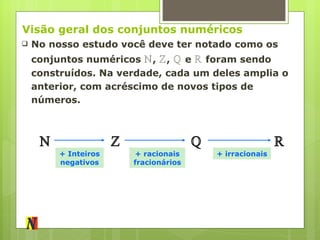
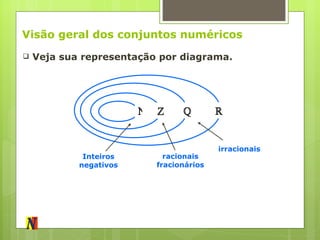
O documento descreve a evolução dos conjuntos numéricos, começando pelos números naturais e chegando aos números reais. Explica como cada novo conjunto foi necessário para resolver problemas matemáticos e como eles se relacionam entre si, com cada um englobando o anterior e acrescentando novos tipos de números.

1. A linguagem dos números

2. Os conjuntos numéricos Como surgiram os números? Eles foram sendo criados pouco a pouco. A cada nova dificuldade ou necessidade, o homem e a ciência foram juntando novos tipos de números aos já existentes. Com o tempo, por questões práticas, foi preciso agrupá-los, formando estruturas com características e propriedades comuns.

3. Conjuntos – Conceitos iniciais Ficaram definidos, assim, os conjuntos numéricos ℕ , dos números naturais ; ℤ , dos números inteiros ; ℚ , dos números racionais ; ℝ , dos números reais ;

4. Conjunto dos números naturais ( ℕ ) A necessidade de contar surgiu com o início da civilização dos povos. Povos primitivos contavam apenas um, dois e muitos. Esses três conceitos, sozinhos, já resolviam seus problemas. Depois outras quantidades (três, quatro, etc.) foram sendo incorporadas. A idéia do zero só surgiu mais tarde. Números utilizados para contar formam o conjunto ℕ dos números naturais, definido assim: ℕ = {0, 1, 2, 3, 4, 5, .. . }

5. Conjunto dos números inteiros ( ℤ ) A soma e o produto de dois naturais são sempre naturais. Mas a diferença de dois naturais nem sempre é natural. Por exemplo, (5 – 2)  ℕ , mas (2 – 5)  ℕ Subtrações como essa última só são definidas com a introdução dos números inteiros negativos (–1, –2, –3, –4, ...). A união dos naturais com os inteiros negativos forma o conjunto ℤ dos números inteiros. ℤ = {..., –3, –2, –1, 0, 1, 2, 3, .. . }

6. Conjunto dos números inteiros ( ℤ ) Podemos separar os inteiros em três categorias: Os positivos : 1, 2, 3, 4, ... O zero : 0 Os negativos : –1, –2, –3, –4, ... De maneira geral, se k é um número inteiro, o número –k também é inteiro. Dizemos que k e –k são simétricos ou opostos .

7. Conjunto dos números inteiros ( ℤ ) Simetria em relação ao zero. 0 -1 -2 -3 -4 1 2 4 3

8. Exemplo De dois inteiros simétricos k e –k, não-nulos, qual é o positivo? Qual o negativo? Dois inteiros simétricos podem ser iguais? A soma, a diferença, o produto e o quociente de dois inteiros são sempre inteiros?

9. Conjunto dos números inteiros ( ℤ ) Definem-se, em ℤ , as relações de igualdade e de ordem (desigualdade). Se p e q são dois inteiros, eles satisfazem uma, e somente uma, das seguintes relações: p = q (p é igual a q); p < q (p é menor que q); p > q (p é maior que q). -> 3 – 5 = 2 -> – 5 < –1 < 0 < 3 -> 7 > 2 > 0 > –4

10. Observação Certos subconjuntos de ℕ e ℤ são definidos por meio de desigualdades. No caso, devemos estar atentos ao universo indicado. Exemplos A = {x  ℕ / x < 4} -> A = {0, 1, 2, 3}. B = {x  ℤ / –3 ≤ x < 2} -> B = {–3, –2, –1, 0, 1}. C = {x  ℤ / x ≥ –2} -> C = {–2, –1, 0, 1, ...}.

11. Observação Os conjuntos numéricos podem vir acompanhados de certos símbolos, que têm a função de excluir, dele, determinados números. Veja: O símbolo asterisco (*) exclui o zero; O símbolo mais (+) exclui os negativos; O símbolo menos (–) exclui os positivos.

12. Observação Quando colocamos os inteiros em ordem crescente, valem os conceitos de antecessor e sucessor . O antecessor de 8 é o 7 e o sucessor de 8 é o 9. Identifique, entre as sentenças a seguir, as que são verdadeiras. O antecessor de –6 é –5 ( ). Se p é inteiro, seu sucessor é (p + 1) e seu antecessor (p – 1) ( ). Se p, é par e q ímpar, então (p + 1).q é impar ( ). Se p é par e q é ímpar, então (p + q).(q + 1) é par ( ). No conjunto dos naturais, 0 não tem antecessor ( ).

13. Conjunto dos números racionais ( ℚ ) A necessidade de operar com grandezas que nem sempre podem ser representadas por números inteiros e, consequentemente exigem subdivisões levou à criação dos números fracionários: 3 5 , 8 7 , 1 10 , etc. Divisões como essas são definidas com a introdução do conceito de número racional .

14. Conjunto dos números racionais ( ℚ ) Todo quociente p/q da divisão de um inteiro p por um inteiro q (q ≠ 0) é chamado de número racional. Veja a definição do conjunto ℚ dos números racionais. ℚ = {x/x = p/q; p, q  ℤ , q ≠ 0}

15. Exemplo São racionais os seguintes números 8 2 = 4 (inteiro) 3 7 (fracionário de termos inteiros) – 3 8 = –0,375 (decimal exato) 5 9 = 0,555... (dízima periódica)

16. Conjunto dos números racionais ( ℚ ) Em resumo, são números racionais Os números inteiros; Os números fracionários; Os decimais exatos; As dízimas periódicas.

17. Transformando decimais exatos em frações Um número decimal exato é sempre igual a uma fração, cujo denominador é uma potência de base 10 e expoente natural. Exemplos 0,35 = 35 10 2 = 35 100 = 7 20 – 1,8 = – 18 10 1 = – 18 10 = – 9 5

18. Transformando decimais periódicos em frações Numa dízima periódica, o grupo de algarismos que se repete é chamado período da dízima. Por exemplo na dízima 23, 4727272..., o período é 72. A fração que dá origem a uma dízima é a sua geratriz.

19. Exemplos Achar a fração geratriz da dízima periódica 0,424242... Suponhamos (1) x = 0,424242... 100 . x = 100 . 0,424242... 100x = 42,4242... ⇒ ⇒ (2) subtraindo (2) – (1) , membro a membro 100x = 42, 4242... – x = 0, 424242... 99x = 42 ⇒ x = 42 99 = 14 33

20. Exemplos Encontrar a fração geratriz da dízima periódica 4,73333... Suponhamos (1) x = 4,73333... 10 . x = 10 . 4,73333... 10x = 47,3333... ⇒ ⇒ (2) subtraindo (2) – (1) , membro a membro 10x = 47,3 3333... – x = 4,7 3333... 9x = 42,6 ⇒ 90x = 426 ⇒ x = 426 90 = 71 15

21. Conjunto dos números racionais ( ℚ ) Podemos representar os números racionais por pontos pertencentes a uma reta orientada, bastando para isso fazer subdivisões convenientes no eixo dos inteiros. 0 -1 -2 -3 1 2 3 0,333... 0,6 – 5/3 1,5 – 6/5

22. Conjunto dos números reais ( ℝ ) Vimos anteriormente, que os únicos números decimais racionais são os exatos e as dízimas periódicas. Existirão números decimais que não sejam exatos nem dízimas? Ou seja, números decimais não-racionais?

23. Conjunto dos números reais ( ℝ ) Veja a figura a seguir. Ela mostra um triângulo retângulo cujos catetos medem 1 unidade. Veja o cálculo de sua hipotenusa. x 1 1 x 2 = 1 2 + 1 2 x 2 = 2 x = √ 2 Extraindo a raiz quadrada de 2 nos levará ao número 1,41421356237 ... que não é racional.

24. Conjunto dos números reais ( ℝ ) Números com √ 2 são chamados de números irracionais. Sua representação decimal não é exata e nem periódica. De modo geral, número irracional é todo número que, escrito na forma decimal, é infinito e não-periódico. Veja alguns exemplos: √ 3 = 1,73205080... 3 √5 = 1,70099759...  = 3,141592653... 0,202202220...

25. Você sabia? que  é aproximadamente 3,1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679821480865132823066470938446095505822317253594081284811174502841027019385211055596446229489549303819644288109756659334461284756482337867831652712019091456485669234603486104543266482133936072602491412737245870066…?

26. Conjunto dos números reais ( ℝ ) A reunião dos racionais com os irracionais resulta no conjunto dos números reais. Ele é a partir de agora, o nosso universo numérico. ℝ = {x/x é racional ou irracional}

27. Visão geral dos conjuntos numéricos No nosso estudo você deve ter notado como os conjuntos numéricos ℕ , ℤ , ℚ e ℝ foram sendo construídos. Na verdade, cada um deles amplia o anterior, com acréscimo de novos tipos de números. ℕ ℤ ℚ ℝ + Inteiros negativos + racionais fracionários + irracionais

28. Visão geral dos conjuntos numéricos Veja sua representação por diagrama. Inteiros negativos racionais fracionários irracionais ℕ ℤ ℚ ℝ

29. Números reais como pontos da reta O conjunto ℝ dos números reais pode ser colocado em correspondência com o conjunto dos pontos de uma reta. Para isso definimos O Um sentido positivo, indicado pela seta; Um ponto O, chamado origem , associado ao zero; uma unidade de medida arbitrária. 1 u A esta reta, damos o nome de reta real ou eixo real ;

30. Números reais como pontos da reta Na reta da figura marcamos os pontos O(0), A(1), B(–3,5), C(4) e D(–2). O 0 A C B D 1 4 – 2 – 3,5 Na representação: A(1), 1 é a abscissa ou a coordenada do ponto A; Em geral : Escrevemos P(x) para indicar que o ponto P está associado ao número x.

31. Números reais como pontos da reta A reta estabelece uma ordenação para os números reais, expressas por relações de desigualdade. Sendo a e b dois reais distintos, temos: a < b (a é menor que b) significa que, na reta real, a está à esquerda de b. a > b (a é maior que b) significa que, na reta real, a está à direita de b.

32. Números reais como pontos da reta Na reta real da figura a seguir, estão representados os números reais 0, p e q. O 0 q p Podemos escrever, por exemplo: p < 0 (p é negativo) q > 0 (q é positivo) p < 0 < q (0 está entre p e q)

33. Observação A relação a ≤ b significa que (a < b ou a = b) e a relação a ≥ b indica que (a > b ou a = b). a ≤ b ( a é menor que ou igual a b ) a ≥ b ( a é maior que ou igual a b ) Exemplos 5 ≥ 3 (5 é maior ou igual a 3) – 2 ≤ 1 (–2 é menor ou igual a 1)

34. Exemplos A figura mostra a reta real, em que O é a origem. São dados os pontos A(a) e B(b) e sabe-se que OA = OC. O C b a A B Quais são as abscissas de dos pontos O e C. Complete os pontilhados com os sinais de desigualdade > ou <. a .... 0 – a .... 0 a + b .... 0 a 2 .... 0 b .... 0 – b .... 0 ab .... 0 – b .... a 0 e –a < > > > > < < <