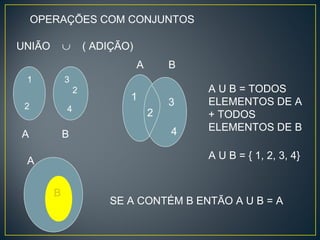
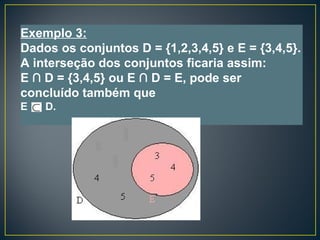
O documento descreve conceitos básicos de conjuntos numéricos e suas operações. Ele define o que é um conjunto, formas de representá-lo e tipos como finito, infinito e vazio. Também explica as relações entre conjuntos como inclusão, igualdade, subconjunto, união, interseção e diferença. Por fim, apresenta exemplos de conjuntos numéricos como naturais, inteiros, racionais, irracionais e reais.

1. CONJUNTOS NUMÉRICOS

2. CONJUNTO
A IDÉIA PRIMITIVA DE CONJUNTO É
UMA REUNIÃO OU COLEÇÃO DE
ELEMENTOS.
- Conjunto de revistas
- Conjunto de alunos de uma escola

3. Formas de representação:
Tabular: ( forma de tabela):
A = { a, e, i, o, u }
B= { 0, 2, 4, 6 }
Diagrama de Venn
a
b
A

4. Representação por meio de propriedade:
A = { x / x tem a propriedade p}
A = { x / x é país da Europa}
Propriedade p
O conjunto A é formado por TODOS os países da Europa.
B = { x / x é número par }
B é formado por todos os números pares.

5. Conjunto vazio:
-Não possui elemento algum
-Representa-se por ∅ ou { }
A = { x / x ∈ IN e 0 . X = 8 } A = ∅
Conjunto finito:
- É todo conjunto onde é possível contar todos os
seus elementos A = { verde, azul, rosa} n(A) = 3
Conjunto infinito:
- É todo conjunto infinito onde não é possível estabelecer
uma contagem dos elementos. B = { 1, 2, 3, 4....}
Conjunto unitário:
-É todo conjunto infinito que possui apenas 1 elemento. B = { 1}

6. RELAÇÃO DE PERTINENCIA E INCLUSÃO
Dado o conjunto A = { 1, a, 2, b, 3, c }
Dizemos que:
O elemento 1 pertence ao conjunto A: 1 ∈ A
4 ∉ A 4 não pertence ao conjunto A
Elemento e conjunto usamos os símbolos ∈ ou
∉
⊄⊂
⊃⊃
∉∈
contidoestánãooucontidoEstá
contémnãoouContém:inclusão
pertencenãoou: pertenceapertinênci

7. SUBCONJUNTO – É PARTE DE UM CONJUNTO
Sendo A = { 0, 1, 2, 3, 4, 5, 6 }
Podemos obter vários subconjuntos a partir de A
B = { 0, 2, 4, 6 } B está contido em A B ⊂ A
ou A contém B A ⊃ B
C = { 4, 5, 7 } C não está contido em A C ⊄ A
Conjunto e conjunto utilizamos a relação de inclusão:
⊂ ⊄ ( está ou não está contido) ⊃ ⊃ ( contém ou não contém)
{ 2, 3, 4 } ⊄ { 0, 3, 6, 8 }

8. A
B
A CONTÉM B A ⊃ B
ou
B ESTÁ CONTIDO EM A B ⊂ A
Em forma de diagrama

9. • Igualdade de conjuntos:
• Dois conjuntos A e B são iguais ( A = B) se
e somente se A tem os mesmos elementos
de B.
Conjunto Universo:
É todo conjunto considerado para
estudar determinada situação:
Exemplo: Ao estudar uma determinada
doença em uma população de ratos, o
conjunto universo é o conjunto de todos
os ratos.

10. Conjuntos Numéricos
I) Números Naturais
N = { 0 , 1 , 2 , 3 , ... }
II) Números Inteiros
Z = { ... , -2 , -1 , 0 , 1 , 2, ... }
Todo número natural é
inteiro, isto é, N é um
subconjunto de Z

11. • III) Números Racionais
• - São aqueles que podemserexpressos na
forma a/b, onde a e b são inteiros
quaisquer, comb diferente de 0.
• Q={x/x = a/b coma e b pertencentes a Z
comb diferente de 0 }

12. -Números decimais exatos são racionais
Pois 0,1 = 1/10
2,3 = 23/10 ...
- Números decimais periódicos são
racionais.
0,1111... = 1/9
0,3232 ...= 32/99
2,3333 ...= 21/9
0,2111 ...= 19/90
-Toda dízima periódica 0,9999 ... 9 ... é uma
outra representação do número 1.

13. IV) Números Irracionais
- São aqueles que não podem ser expressos
na forma a/b, com a e b inteiros e b
diferente de 0.
-São compostos por dízimas infinitas não
periódicas.
Ex:

14. V) Números Reais
- É a reunião do conjunto dos números
irracionais com o dos racionais.
Resumindo:

15. Vejamos primeiramente o conceito de
par ordenado:
• Dados dois números x e y numa certa
ordem, chamamos de par ordenado
( x,y) ao par de números x e y , tais
que x é o 1º elemento do par e y é o
2º elemento do par ordenado.
• Exemplo: ( 2, 3 ) x = 2 e y = 3
( - 5 ; 3,2 ) x = -5 e y = 3,2

16. Produto cartesiano A x B é o produto deProduto cartesiano A x B é o produto de
A por B, formado por pares ordenados A por B, formado por pares ordenados
onde onde
o 1º elemento pertence ao 1º conjunto e o 1º elemento pertence ao 1º conjunto e
o 2º elemento pertence ao 2º conjunto. o 2º elemento pertence ao 2º conjunto.

17. Sendo conhecidos os conjunto A e B:
A = { 3, 4, 5 } e B = { 1, 2 }
Em diagrama:Em diagrama:
3
4
5
1
2
A B
A x B
AXB= { (3,1), (3,2), (4,1),(4,2),(5,1),(5,2) }

18. OPERAÇÕES COM CONJUNTOS
UNIÃO ∪ ( ADIÇÃO)
A B
A U B = TODOS
ELEMENTOS DE A
+ TODOS
ELEMENTOS DE B
1
2
3
4
2
A U B = { 1, 2, 3, 4}
A
B
SE A CONTÉM B ENTÃO A U B = A
A B
1
2
3
4

19. Exemplo 1:
Dados os conjuntos A = { x | x é inteiro
e -1 < x < 2} e B = {1,2,3,4} a união
desses dois conjuntos é :
A U B = {0,1,2,3,4}
Exemplo 2:
Dados os conjuntos A = {1,2,3} e B =
{1,2,3,4,5} a união desses conjuntos é:
A U B = {1,2,3,4,5}, nesse caso podemos
dizer que
A U B = B.

20. INTERSECÇÃO ∩
SÃO OS ELEMENTOS QUE APARECEM NOS DOIS
CONJUNTOS AO MESMO TEMPO
a
b c
d
e
A ∩ B = { C }
A
B A ∩ B = B
A B

21. Os elementos que fazem parte do conjunto interseção
são os elementos comuns aos conjuntos relacionados.
Exemplo 1:
Dados dois conjuntos A = {5,6,9,8} e B = {0,1,2,3,4,5}, se
pedimos a interseção deles teremos:
A ∩ B = {5}, dizemos que A “inter” B é igual a 5.

22. Exemplo 2:
Dados os conjuntos B = {-3, -4, -5, -6} e C = {-7,
-8, -9}, se pedirmos a interseção deles
teremos:
B ∩ C = { } ou B ∩ C = , então B e C são
conjuntos distintos.

23. Exemplo 3:
Dados os conjuntos D = {1,2,3,4,5} e E = {3,4,5}.
A interseção dos conjuntos ficaria assim:
E ∩ D = {3,4,5} ou E ∩ D = E, pode ser
concluído também que
E D.

24. Dados dois conjuntos A e B chama-se conjunto diferença
ou diferença entre A e B o conjunto formado pelos
elementos de A que não pertencem a B.
O conjunto diferença é representado por A – B.
Exemplo 1:
A = {1,2,3,4,5} e B = {3,4,5,6,7} a diferença dos conjuntos
é:
A – B = {1,2}

25. Exemplo 2:
A = {1,2,3,4,5} e B = {8,9,10} a diferença dos conjuntos é:
A – B = {1,2,3,4,5}
Exemplo 3:
A = {1,2,3} e B = {1,2,3,4,5}a diferença dos conjuntos é:
A – B =

26. DIFERENÇA A – B OU B – A
A – B ( TODOS ELEMENTOS QUE APARECEM
EM A MAS NÃO ESTÃO EM B )
1
2
3
4
5
6
A B
A – B = { 1, 2}
B – A = { 5, 6 }

27. CONJUNTO COMPLEMENTAR
Complemento é aquilo que completa
B
CA
Lemos Complementar de A em
relação a B B – A
Toda parte azul é o
complementar de A
A
B
ELEMENTOS QUE
ESTÃO EM B MAS
NÃO ESTÃO EM A

28. Exemplo 4:
Dados os conjuntos A = {1,2,3,4,5,6} e B
= {5,6}, a diferença dos conjuntos é:
A – B = {1,2,3,4}. Como B A podemos
escrever em forma de complementar:
A – B = A
B = {1,2,3,4}.
Lemos: complementar de B em relação a A
São todos elementos que estão em A mas não
estão em B

29. • Intervalos Reais
• O conjunto dos números reais (IR)
possui subconjuntos, denominados
intervalos. Estes intervalos são
determinados pormeio de
desigualdades.
• Sejamos números reais a e b,
com a < b , temos os conjuntos:

30. OBSERVAÇÃO:
A bolinha vazia na reta real indica que os extremos a e b
não pertencem ao intervalo.
A bolinha cheia na reta real indica que os extremos a e b
pertencem ao intervalo.

34. • Existem, também, os intervalos
infinitos. São eles:
• 5 - Menos infinito e fechado em n :

35. • 6 - Menos infinito e aberto em n :

36. • 7 - Mais infinito e fechado em n

37. • 8 - Mais infinito e aberto em n :

38. • Prof. Meire de Fátima
• Ensino Médio – 1º ano
• 2011