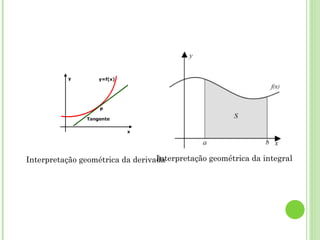
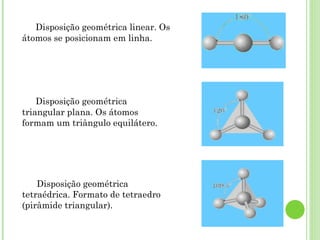
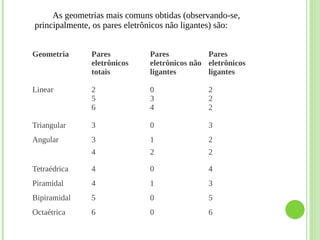
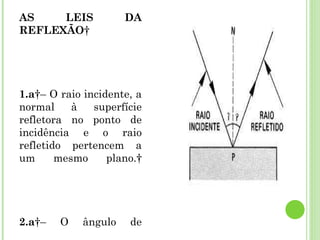
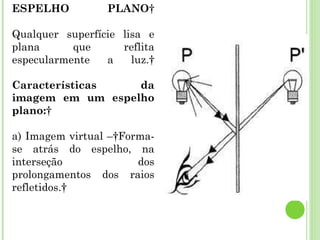
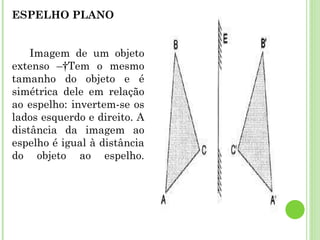
O documento discute as relações entre geometria e outras áreas como matemática, física, química e astronomia. Apresenta como a geometria contribui para o desenvolvimento do cálculo e como este é aplicado em diversas ciências. Também aborda conceitos geométricos importantes como geometria analítica, molecular, diferencial e óptica geométrica.

1. Universidade Federal Rural do Rio de Janeiro I nstituto de Ciências Exatas Departamento de Matemática A Geometria e as Ciências Experimentais Docente : Renato Machado Aquino Discentes: Allexsandro Martins 2010190031 André Rocha 2010190058 Ismael Ledoino 2010190287 Mauricio Petroceli 2010190457 Disciplina : Geometria Euclidiana Plana

2. INTRODUÇÃO Os objetos geométricos surgem ao nossos olhos quando contemplamos o mundo a nossa volta. Circunferências, triângulos, elipses, esferas estão ao alcance da vista de qualquer um que o contemple. Por isso é impossível desassociar a geometria das ciências naturais. É de se esperar que as ciências que estudam o nosso mundo se depare uma vez ou outra com o objeto de estudo da geometria.

3. Geometria e matemática

4. A matemática é ciência natural? Embora o objeto de estudo da matemática seja abstrato, não os encontrando, em si, no mundo natural, são inegáveis as aplicações da matemática nas ciências naturais. Então, se não for possível considerá-la como tal, deve-se verificar a importância fundamental da matemática para estas ciências. “ Uma ciência natural é, apenas, uma ciência matemática.” Emanuel Kant

5. A geometria e o desenvolvimento do Cálculo A geometria está diretamente ligada à origem da própria matemática, mas talvez, a área da matemática que encontrou maiores aplicações nas ciências naturais tenha sido o Cálculo. Vale lembrar que as ideias de derivada e integral, primordiais no Cálculo, surgiram diretamente das conceitos de reta tangente a uma curva e cálculo da área de uma figura, problemas clássicos da geometria.

6. Interpretação geométrica da derivada Interpretação geométrica da integral

7. Cálculo aplicado Problemas de diversas áreas são modelados por funções oriundas de soluções de equações diferenciais ordinárias ou parciais.

8. Derivadas e integrais estão presentes nas maiorias das equações da física.

9. Funções trigonométricas que são de origem profundamente geométricas são de vital importância no Cálculo.

10. Geometria Analítica Área da matemática de forte influência geométrica com grande aplicação no Cálculo e, por consequência, em muitas das ciências naturais.

11. Procura dar uma forma algébrica a geometria.

12. Superfícies geométricas e respectivas relações algébricas

13. Consideração importante A relação entre geometria e matemática permite não só resolver problemas puramente geométricos com álgebra como também problemas puramente algébricos com geometria. Existe um momento onde é impossível isolar a geometria das outras áreas da matemática.

14. QUÍMICA E GEOMETRIA A geometria é uma ferramenta preciosa para entendermos o universo. Ela nos ajuda tanto a descrever a grandeza cósmica das órbitas planetárias quanto nos auxilia na visão do inimaginavelmente pequena das formas das moléculas.

15. A geometria molecular baseia-se na forma espacial que as moléculas assumem pelo arranjo dos átomos ligados. Assim, cada molécula apresenta uma forma geométrica característica da natureza das ligações (iônicas ou covalentes) e dos constituintes (como elétrons de valência e eletronegatividade). A teoria da repulsão dos pares eletrônicos de valência (TRPEV) aponta que os pares eletrônicos (elétrons de valência, ligantes ou não) do átomo central se comportam como nuvens eletrônicas que se repelem e, portanto, tendem a manter a maior distância possível entre si. Mas, como as forças de repulsão eletrônica não são suficientes para que a ligação entre os átomos seja desfeita, essa distância é verificada no ângulo formado entre eles. O efeito das zonas de repulsão tende a formar três disposições geométricas básicas em um molécula apolar (aquela na qual os elétrons não se concentram em pólos): a linear, a triangular plana e a tetraédrica, conforme as três figuras a seguir: Geometria Molecular.

16. Disposição geométrica linear. Os átomos se posicionam em linha. Disposição geométrica triangular plana. Os átomos formam um triângulo equilátero. Disposição geométrica tetraédrica. Formato de tetraedro (pirâmide triangular).

17. As geometrias mais comuns obtidas (observando-se, principalmente, os pares eletrônicos não ligantes) são: Geometria Pares eletrônicos totais Pares eletrônicos não ligantes Pares eletrônicos ligantes Linear 2 5 6 0 3 4 2 2 2 Triangular 3 0 3 Angular 3 4 1 2 2 2 Tetraédrica 4 0 4 Piramidal 4 1 3 Bipiramidal 5 0 5 Octaétrica 6 0 6

18. FÍSICA E GEOMETRIA Toda a minha Física não passa de uma Geometria. Descartes

19. geometria diferencial Geometria Diferencial é o ramo da Geometria no qual os conceitos de Cálculo são aplicados a curvas, superfícies e outros objetos geométricos. A Geometria Diferencial clássica usa a geometria de coordenadas, como geometria analítica, coordenadas cartesianas, etc., embora no século XX os métodos de Geometria Diferencial tem sido aplicados a outras áreas de Geometria, como Geometria Projetiva. A Geometria Diferencial foi estudada por Gaspard Monge e Carl F. Gauss no início do século XIX. Trabalhos importantes no século XIX foram feitas por matemáticos como: B. Riemann, E. B. Christoffel e C. G. Ricci, que foram colecionados e sistematizados no final do século por J. G. Darboux e Luigi Bianchi. A importância da Geometria Diferencial é vista no estudo da Teoria da Relatividade Geral que Einstein formulou inteiramente em função da Geometria Diferencial de uma variedade tetra-dimensional combinando espaço e tempo, usando a notação tensorial.

20. Relatividade Geral A Relatividade Geral é uma generalização da primeira ( a Relatividade Especial que diz “ o espaço e o tempo são faces distintas de uma única estrutura que denominamos espaço-tempo”). O espaço-tempo nada mais é do que um conjunto de pontos que obedecem a certas relações. Os pontos do espaço-tempo são denominados eventos. Precisamos de quatro números para localizar um ponto no espaço-tempo. Não é por acaso que quando marcamos um encontro precisamos fixar, em geral, um conjunto com quatro informações: o logradouro, o número, o andar, e o horário. Matematicamente isso é codificado dizendo-se que o espaço-tempo possui quatro dimensões. A evolução de uma partícula pontual, por exemplo, será representada por uma linha no espaço-tempo (como na figura).

21. Óptica Geométrica Estuda as leis que descrevem o comportamento geométrico da luz nos fenômenos ópticos. Reflexão da luz – Fenômeno óptico que ocorre quando a luz, ao incidir em uma superfície que separa dois meios, volta ao meio original. a) Reflexão difusa – Efetua-se em todas as direções, como a reflexão produzida por todos os corpos que não apresentam uma superfície polida como um espelho (esta página que você está lendo, por exemplo). b) Reflexão especular – Ocorre quando um feixe incide numa superfície polida e volta regularmente para o meio original; por exemplo, se o feixe incidente é paralelo, o refletido também é paralelo. A reflexão especular permite a formação de imagens.

22. AS LEIS DA REFLEXÃO 1.a – O raio incidente, a normal à superfície refletora no ponto de incidência e o raio refletido pertencem a um mesmo plano. 2.a – O ângulo de incidência é igual ao ângulo de reflexão (figura).

23. ESPELHO PLANO Qualquer superfície lisa e plana que reflita especularmente a luz. Características da imagem em um espelho plano: a) Imagem virtual – Forma-se atrás do espelho, na interseção dos prolongamentos dos raios refletidos.

24. ESPELHO PLANO Imagem de um objeto extenso – Tem o mesmo tamanho do objeto e é simétrica dele em relação ao espelho: invertem-se os lados esquerdo e direito. A distância da imagem ao espelho é igual à distância do objeto ao espelho.

25. A GEOMETRIA DOS ASTROS A sabedoria da natureza é tal que não produz nada de supérfluo ou inútil. Nicolau Copérnico

26. Astronomia, que etimologicamente significa “ lei das estrelas " é hoje uma ciências que se abre num leque de categorias complementares aos interesses da geografia, da física, da matemática. Envolve diversas observações procurando respostas aos fenômenos físicos que ocorrem dentro e fora da Terra bem como em sua atmosfera e estuda as origens, evolução e propriedades físicas e químicas de todos os objetos que podem ser observados no céu (e estão além da Terra), bem como todos os processos que os envolvem.

27. A Teoria Heliocêntrica É a teoria que o Sol está estacionário no centro do universo. Historicamente, o heliocentrismo era oposto ao geocentrismo, que colocava a Terra no centro. Apesar das discussões da possibilidade do heliocentrismo datarem da antiguidade clássica, somente 1.800 anos mais tarde, no século XVI, que o matemático e astrônomo polonês Nicolau Copérnico apresentou um modelo matemático preditivo completo de um sistema heliocêntrico. Copérnico calculou os períodos de revolução do planetas e suas distâncias ao Sol, admitindo órbitas circulares centradas no Sol e movimentos uniformes dos planetas em suas órbitas.

28. Aplicação da geometria no cálculo de distâncias entre o sol e planetas Imaginemos, como ilustra a figura, que Marte em M esteja em oposição, em a Terra estando em T e o Sol em S. Sabemos, por dados de observação, que 106 dias após, a Terra e Marte se encontrarão em posições 7" e M’, respectivamente, tais que ST´M´ = 90. Durante esse tempo, o ângulo α, descrito pela Terra, é de aproximadamente 105°, como é fácil calcular (pois α: 106 = 360° : 365). Quanto a Marte, ele terá descrito um ângulo β ≈ 56 pois Como conseqüência, T’SM’ = 105 – 56 = 490. Finalmente, o triângulo retângulo ST’M’ nos dá: Fica assim calculada a distância de Marte ao Sol como 1,5 vezes a distância da Terra ao Sol.

29. A geometria e o universo Ao que se sabe, as secções cônicas começaram a ser estudadas pelo menos no século III a.C., muito embora tenham sido particularmente utilizadas pelos matemáticos e astronomos do século XVII quando estes procuravam equacionar movimentos de vários objetos naturais. No início do Renascimento, Nicolau Copérnio afirmava que as órbitas dos planetas então conhecidos eram circulares .