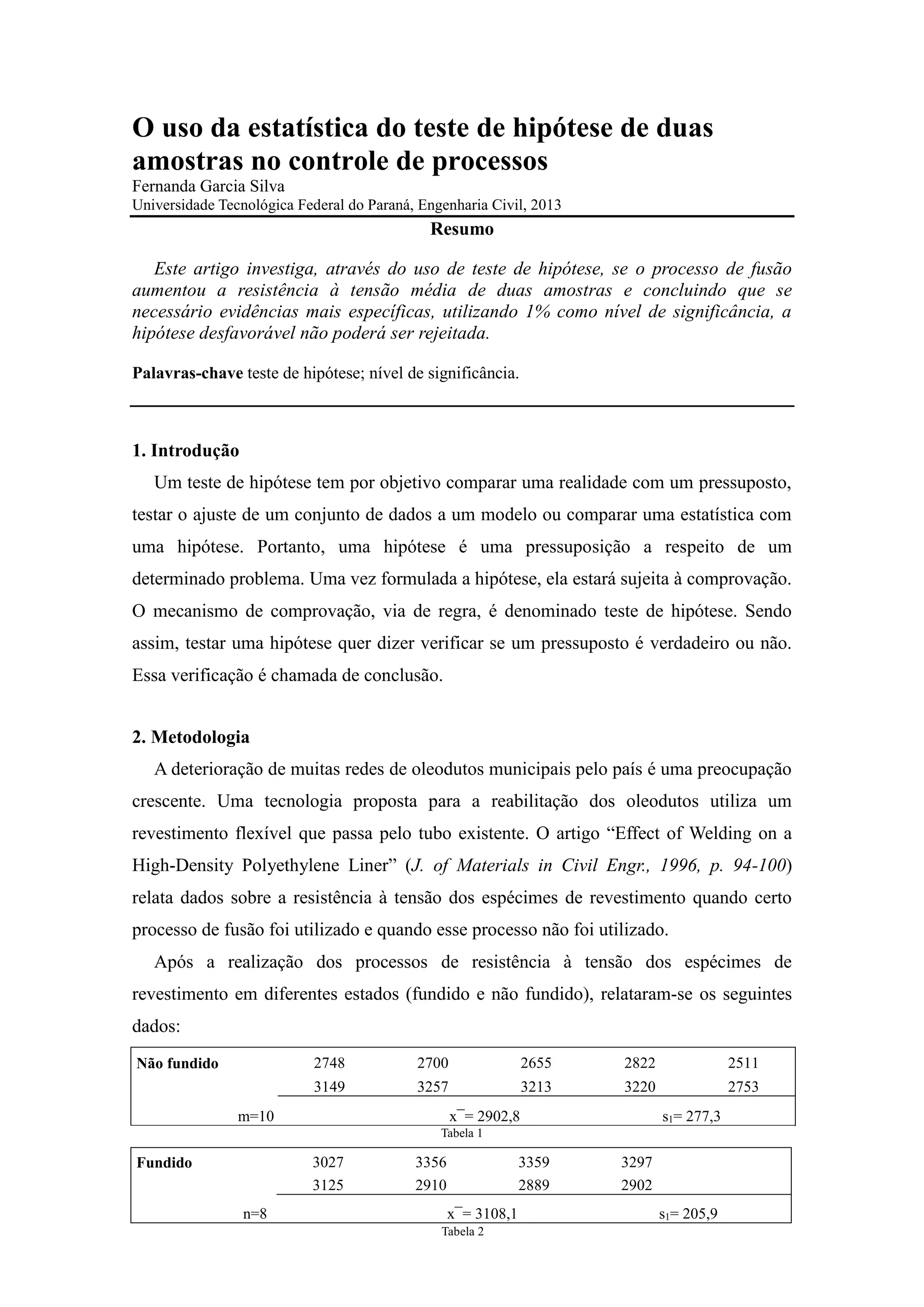
Este documento descreve um estudo que usou um teste de hipótese para determinar se um processo de fusão aumentou a resistência à tensão média de amostras. Os resultados mostraram que a resistência à tensão média das amostras fundidas foi maior do que as não fundidas, confirmando a conclusão do estudo original com um nível de significância de 5%. No entanto, com um nível de 1%, a hipótese nula de que não houve diferença não poderia ser rejeitada.

1. O uso da estatística do teste de hipótese de duas
amostras no controle de processos
Fernanda Garcia Silva
Universidade Tecnológica Federal do Paraná, Engenharia Civil, 2013
Resumo
Este artigo investiga, através do uso de teste de hipótese, se o processo de fusão
aumentou a resistência à tensão média de duas amostras e concluindo que se
necessário evidências mais específicas, utilizando 1% como nível de significância, a
hipótese desfavorável não poderá ser rejeitada.
Palavras-chave teste de hipótese; nível de significância.
1. Introdução
Um teste de hipótese tem por objetivo comparar uma realidade com um pressuposto,
testar o ajuste de um conjunto de dados a um modelo ou comparar uma estatística com
uma hipótese. Portanto, uma hipótese é uma pressuposição a respeito de um
determinado problema. Uma vez formulada a hipótese, ela estará sujeita à comprovação.
O mecanismo de comprovação, via de regra, é denominado teste de hipótese. Sendo
assim, testar uma hipótese quer dizer verificar se um pressuposto é verdadeiro ou não.
Essa verificação é chamada de conclusão.
2. Metodologia
A deterioração de muitas redes de oleodutos municipais pelo país é uma preocupação
crescente. Uma tecnologia proposta para a reabilitação dos oleodutos utiliza um
revestimento flexível que passa pelo tubo existente. O artigo “Effect of Welding on a
High-Density Polyethylene Liner” (J. of Materials in Civil Engr., 1996, p. 94-100)
relata dados sobre a resistência à tensão dos espécimes de revestimento quando certo
processo de fusão foi utilizado e quando esse processo não foi utilizado.
Após a realização dos processos de resistência à tensão dos espécimes de
revestimento em diferentes estados (fundido e não fundido), relataram-se os seguintes
dados:
Não fundido 2748 2700 2655 2822 2511
3149 3257 3213 3220 2753
m=10 x ̅ = 2902,8 s1= 277,3
Tabela 1
Fundido 3027 3356 3359 3297
3125 2910 2889 2902
n=8 x ̅ = 3108,1 s1= 205,9
Tabela 2

2. Na construção do gráfico, é possível notar um padrão linear que sustenta a suposição
de que as distribuições de resistência à tensão sob as duas condições são normais.
Segundo os autores do artigo em análise, o processo de fusão aumentou a resistência
à tensão média. Contudo, faremos um teste de hipóteses para julgar se os dados
sustentam essa conclusão.
3. Resultados e Discussões
3.1. Sejam: µ1 a resistência à tensão média real de espécimes, quando o tratamento sem
união é usado, e por µ2 a resistência à tensão média real quando o tratamento não é
usado.
3.2. H0: µ1 - µ2 = 0 (nenhuma diferença nas resistências à tensão médias reais dos dois
tratamentos)
3.3. H1: µ1 - µ2 < 0 (a resistência à tensão média real do tratamento não fundido é menor
que a do tratamento de união, de modo que a conclusão dos investigadores está correta)
3.4. O valor nulo é Δ0 = 0, assim a estatística de teste é:
𝑡 =
𝑥̅ − 𝑦̅
√1
𝑚
𝑠1
2
+
1
𝑛
𝑠2
2
3.5. Calculamos agora o valor da estatística de teste e o gl para o teste:
𝑡 =
2902,8 − 3108,1
√(277,3)2
10
+
(205,9)2
8
=
−205,3
113,97
= −1,8
Usando
1
𝑚
𝑠1
2
= 7689,529 e
1
𝑛
𝑠2
2
= 5299,351,
𝑣 =
(7689,529 + 5299,351)2
(7989,529)2
9 +
(5299,351)2
7
=
168.711.003,7
10.581.747,35
= 15,94
assim, o teste se baseará no gl 15.
3.6. Por valor tabelado, tem-se que a área sob a curva t do gl 15 à direita de 1,8 é 0,046,
assim o valor P para um teste de cauda inferior também é de 0,046.

3. 4. Conclusão
Usando um nível de significância de 0,05 (5%), podemos rejeitar apenas a hipótese
nula em favor da hipótese alternativa, confirmando a conclusão do artigo. Entretanto,
uma pessoa que necessite de mais evidências pode selecionar α = 0,01 (1%), um nível
para o qual o H0 não pode ser rejeitado.
5. Referências
DEVORE, Jay L.; Probabilidade e estatística para engenharia e ciências, 6 ª Ed., São
Paulo: Cengage Learning, 2011.
http://www.ebah.com.br/content/ABAAAAy5kAL/teste-hipoteses
BAKEER, R. and BARBER, M. (1996). ”Effect of Welding on a High-Density
Polyethylene Liner.” J. Mater. Civ. Eng., 8(2), 94–100.
MORETIN, Luiz G.; Estatística básica: probabilidade e inferência, volume único, São
Paulo: Pearson Prentice Hall, 2010.