O documento descreve o algoritmo de Rabin-Karp para busca de padrões em strings. O algoritmo usa hashing para representar substrings do texto e a string padrão como valores numéricos, e compara esses valores em vez de comparar os caracteres diretamente. Isso reduz o número de comparações necessárias em média e no melhor caso para O(m+n). O documento também apresenta exemplos e compara o desempenho de Rabin-Karp com outros algoritmos de busca de padrão.

1. Algoritmo de Rabin-Karp
LORRAN PEGORETTI
MATHEUS LANI REGATTIERI ARRAIS
TRABALHO REALIZADO PARA AVALIAÇÃO NA DISCIPLINA DE PROJETO E ANÁLISE DE
ALGORITMOS, DO CURSO DE CIÊNCIA DA COMPUTAÇÃO, TURNO MATUTINO, DA
UNIVERSIDADE DE VILA VELHA (UVV), MINISTRADA PELO PROFESSOR ALESSANDRO BERTOLANI.
2013

2. Tópicos Abordados
 Descrição do Problema Original
 Descrição do Algoritmo Rabin-Karp
 Descrição de Estratégia
 Pseudocódigo
 Funcionamento do Algoritmo
 Identificação dos conceitos estratégicos
 Complexidade
 Exemplos
 Conclusões
 Trabalho Similares/Futuros
 Referências

3. Descrição do Problema Original
Busca por padrão de Strings
 O problema consiste em dado o texto T e o padrão P encontrar
todas as ocorrências de P dentro de T.
 Todo s tal que T[s + 1…s + m] = P [1...m], onde s é o índice de cada
ocorrência e m é o tamanho do padrão P.
 Busca em um texto dinâmico através de um algoritmo aquele que
não se tem informações prévias sobre ele.
 Existem cinco algoritmos: Força Bruta, Rabin-Karp, busca por
Autômato, Knuth-Morris-Pratt e Boyer-Moore.

4. Descrição do Algoritmo Rabin-Karp
 Trata cada substring de tamanho M do texto como uma tabela de
dispersão (hash).
 Padrão é encontrado quando a chave da substring coincide com a do
padrão.
 Com tabela virtual: tamanho elevado reduz probabilidade de falsas
escolhas.
 Evolução do Força Bruta, ao invés de comparar a janela com o padrão
caracter a caracter, é proposto usar uma comparação numérica entre
os restos da divisão por um mesmo inteiro da janela e do padrão.

5. Descrição do Algoritmo
 No Força-Bruta a cada deslocamento pode acabar fazendo muitas
comparações antes de descobrir que uma janela não é uma
ocorrência, no Rabin-Karp ele tenta evitar a comparação caracter
a caracter das janelas que não são ocorrências.
 Quando o valor numérico da janela e do padrão forem diferentes,
necessariamente o conteúdo da janela e do padrão também
devem ser diferentes.
 Notação utilizada:
 n: numero de caracteres do texto
 m: numero de caracteres da palavra
 d: cardinalidade do alfabeto ∑
 q: numero primo, como: 16.647.133
 T: string do texto
 P: string da palavra

6. Descrição da Estratégia
 Ideia de Programação Dinâmica e Força-Bruta
 O algoritmo de Rabin-Karp usa a ideia de “Impressão digital”
 Em aplicações envolvendo objetos longos, como por exemplo,
longas cadeias de caracteres, pode-se representar tais objetos por
“impressões digitais” curtas. Uma impressão digital pode ser um
valor numérico atribuído a cada objeto por uma função de
espalhamento, por exemplo. O importante é que dois objetos
distintos tenham pouca chance de ter a mesma impressão digital,
de maneira que, para decidir se dois tais objetos são iguais,
possamos comparar não os objetos, mas suas impressões digitais

7. Objetivo
 Através de técnicas hashing processar uma função de assinatura
de cada substring de m-caracteres do texto e checar se é igual à
assinatura da palavra procurada.
 Função: h(k) = k mod q, onde q é um numero primo grande
 Método: baseado no processamento da função para a posição i dando
o valor para a posição i – 1. Usa-se um valor elevado de q para evitar
colisões aleatórias. Busca-se diretamente fazer uma comparação entre
a palavra e a substring

8. Pseudocódigo
RABIN-KARP-MATCHER (T, P, d, q)
(1) n  tamanho [T];
(2) m  tamanho [P];
(3) h  dm-1
mod q;
(4) p  0;
(5) t0  0
(6) for i  1 to m
(7) do p  (dp + P[i]) mod q;
(8) t0  (dt0 + T[i]) mod q;
(9) for s  0 to n - m
(10) do if p = ts
(11) then if P[1..m] = T[s + 1..s + m]
(12) then “Encontrou a palavra”;
(13) if s < n – m
(14) then ts+1  (d(ts – T[s + 1]h) + T[s + m + 1]) mod q;

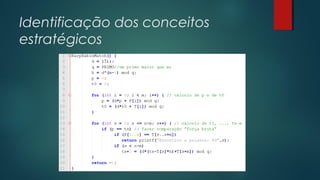
9. Funcionamento do Algoritmo
 Linhas[1-5]: inicialização das variáveis. É importante ressaltar que a
implementação da função hash é arbitraria;
 Linhas [6-8]: iteração com índice relacionado à cardinalidade da palavra.
O bloco inicializa o hash(p) da palavra e do texto, hash(t);
 Linhas [9-14]: iteração de comparação; na linha 10 em caso da
comparação ser valida tem a possibilidade da substring encontrada ser a
procurada. Observa-se que esta linha apresenta o caráter probabilístico
do algoritmo. Uma comparação extra é realizada para confirmar o
resultado; não comparando a hash como na anterior, mas os caracteres
da substring com a palavra.
 Em caso negativo da comparação, temos um novo valor de hash(t) para
a substring, realizando a iteração ate encontrar a palavra(s) ou se esgotar
o texto.

10. Identificação dos conceitos
estratégicos

11. Complexidade
 Pior Caso: é O((n – m + 1)m), podendo ser reduzida a O(nm), este
caso ocorreria quando o numero de colisões fosse elevado, o que
obrigaria o algoritmo a realizar um maior numero de comparações e
operações para se obter um novo valor de hash(t).
 Nos casos médio e melhor: este algoritmo trabalha em O(m + n). A
prova para estes casos é complicada, devido principalmente ao
caráter probabilístico deste algoritmo, pode-se obter demonstração
em [Cor97].
 Apesar de ser probabilístico este algoritmo não se apresenta eficiente
na busca de textos que estejam em constante mudança, já para
textos que não são modificados constantemente ele poderá
apresentar um desempenho melhor devido ao aproveitamento da
tabela hash, para encontrar estas palavras.

12. Exemplo

13. Exemplo

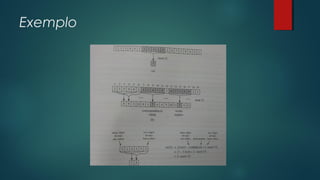
14. Exemplo
 Ao padrão P = 31415 corresponde o valor decimal p = 31.415
 Seja T = 123141567, então:
 T[1..5] = 12314 e t0 = 12314
 T[2..6] = 23141 e t1 = 23141
 T[3..7] = 31415 e t2 = 31415
 T[4..8] = 14156 e t3 = 14156
 T[5..9] = 41567 e t4 = 41567

15. Conclusões
 Tenta diminuir o numero de comparações através do calculo de um hash da palavra
procurada e da substring, porem através deste procedimento ele se torna probabilístico
 Os cálculos de p e t0 gastam tempo O(m)
 Os cálculos de t1, ..., tn-m mais a eventual comparação por “força-bruta”, gastam tempo
O((n - m)m)
 Numero máximo de deslocamentos s válidos é n – m +1
 Tempo total do algoritmo de Rabin-Karp é O(nm)
 Na prática, o algoritmo tem bom desempenho
 Ele é válido para qualquer alfabeto, bastando apenas interpretar cada caractere
como um dígito

16. Trabalhos Similares/Futuros
 Knuth-Morris-Pratt: considerado o algoritmo de “força bruta”, quando
ocorre uma diferença entre T[i] e P[j], evitar comparações
redundantes. Função de falha onde o pré-processamento em P
determina se seus prefixos aparecem como subsequência dele mesmo,
será definido também como o tamanho o maior prefixo de P[0..k] que
é sufixo de P[1..k].
 É pré-calculado apenas o que pode ser reaproveitado da
comparação anterior, independente do próximo caracter .
 Boyer-Moore: baseia-se na alta probabilidade de encontrar diferenças
em alfabetos grandes, por isso, P é comparado com T de trás para
frente, quando se encontra uma diferença em T[i], o padrão P dará um
salto à frente, considerando-se as comparações já realizadas

17. Comparações
Foi usado linguagem Java, S.O Ubuntu 12.04, notebook Core2Duo
com 4Gb de memória.
Os resultados apresentados abaixo são correspondentes à pesquisa
da palavra ’Capitu’ pelo livro ’Dom Casmurro’ de Machado de Assis.
A cópia utilizada possuí 371.457caracteres enquanto o padrão possui
6 caracteres, há 335 ocorrências no texto.
Forca Bruta
 Tempo médio total: 6,4 ms
 Número de comparações na busca: 745,399
 Número de comparações total: 745,399
Rabin-Karp
 Tempo médio total: 6,8 ms
 Número de comparações na busca: 374,405
 Número de comparações total: 374,405

18. Comparações
 KMP
 Tempo médio total: 5,86 ms
 Número de comparações na busca: 745,409
 Número de comparações total: 745,414
 Boyer Moore
 Tempo médio total: 3,2 ms
 Número de comparações na busca: 142,929
 Número de comparações total: 142,939

19. Referências
 CORMEN, T., Leiserson, C., e Rivest, R. 1997. “Introduction to
Algortihms”, em The Rabin-Karp algorithm, pp. 857-883.
 BAEZA-YATES, R., Frakes, W. 1992. “Information Retrieval Data
Strucures & Algorithms” em String Searching Algorithms,pp. 219-237.
 KNUTH, D. E. The Art of Computer Programming. Massachusetts:
Addison-Wesley Longman, 1997. v. 1 e 2.
 ZIVIANI, N. Projeto de Algoritmos - Com Implementações em
PASCAL e C. São Paulo: Editora Pioneira, 1999.