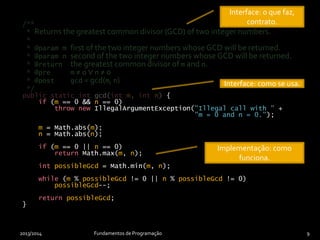
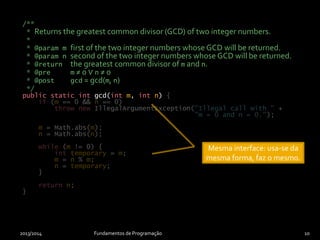
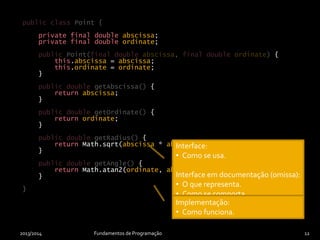
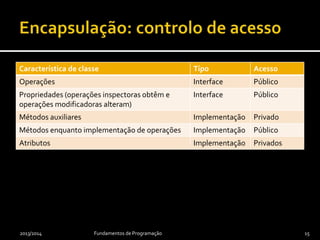
O documento discute os conceitos de encapsulamento, cópia e igualdade de instâncias em programação orientada a objetos. Apresenta como encapsulamento aplica o conceito de ocultação de informação para separar a interface de uma classe de sua implementação. Também explica a necessidade de construtores de cópia e métodos de igualdade para comparar e copiar instâncias corretamente.

1. Encapsulação
Cópia de instâncias
Igualdade de instâncias

2.  Operação toString
 Classes, instâncias e objectos
 Leituras com Scanner
2013/2014 Fundamentos de Programação 2

3.  Aplica ocultação de informação a elemento de
linguagem
 Oculta implementação e revela interface
 Produtores: acesso exclusivo à implementação
 Consumidores ou clientes: acedem apenas a interface
 Resultado são módulos
 Rotinas
 Objectos/classes
 Pacotes
2013/2014 Fundamentos de Programação 3
Ou «encapsulamento».
A ver mais tarde.

4.  Interface
 Como se usa?
 O que faz?
 Qual o contrato entre produtor e consumidor?
 Implementação
 Como funciona?
 Qual o mecanismo?
2013/2014 Fundamentos de Programação 4

5.  Implementação pode mudar sem afectar
consumidores
 Produtores podem garantir bom
comportamento dos módulos
 Mais fácil localizar erros
 Mais fácil corrigir erros
 Facilita abstracção do consumidor!
2013/2014 Fundamentos de Programação 5

6.  Métodos e rotinas
 Cabeçalho apenas
 Classes
 Operações
 Propriedades
 …
2013/2014 Fundamentos de Programação 6

7.  Métodos e rotinas
 Corpo apenas
 Classes
 Métodos auxiliares
 Métodos enquanto implementação de operações
 Atributos
 …
2013/2014 Fundamentos de Programação 7

8. 2013/2014 Fundamentos de Programação 8

9. {
if (m == 0 && n == 0)
throw new IllegalArgumentException("Illegal call with " +
"m = 0 and n = 0.");
m = Math.abs(m);
n = Math.abs(n);
if (m == 0 || n == 0)
return Math.max(m, n);
int possibleGcd = Math.min(m, n);
while (m % possibleGcd != 0 || n % possibleGcd != 0)
possibleGcd--;
return possibleGcd;
}
/**
* Returns the greatest common divisor (GCD) of two integer numbers.
*
* @param m first of the two integer numbers whose GCD will be returned.
* @param n second of the two integer numbers whose GCD will be returned.
* @return the greatest common divisor of m and n.
* @pre m ≠ 0 ∨ n ≠ 0
* @post gcd = gcd(m, n)
*/
public static int gcd(int m, int n)
2013/2014 Fundamentos de Programação 9
{
if (m == 0 && n == 0)
throw new IllegalArgumentException("Illegal call with " +
"m = 0 and n = 0.");
m = Math.abs(m);
n = Math.abs(n);
if (m == 0 || n == 0)
return Math.max(m, n);
int possibleGcd = Math.min(m, n);
while (m % possibleGcd != 0 || n % possibleGcd != 0)
possibleGcd--;
return possibleGcd;
}
Interface: como se usa.
Interface: o que faz,
contrato.
Implementação: como
funciona.

10. /**
* Returns the greatest common divisor (GCD) of two integer numbers.
*
* @param m first of the two integer numbers whose GCD will be returned.
* @param n second of the two integer numbers whose GCD will be returned.
* @return the greatest common divisor of m and n.
* @pre m ≠ 0 ∨ n ≠ 0
* @post gcd = gcd(m, n)
*/
public static int gcd(int m, int n)
2013/2014 Fundamentos de Programação 10
{
if (m == 0 && n == 0)
throw new IllegalArgumentException("Illegal call with " +
"m = 0 and n = 0.");
m = Math.abs(m);
n = Math.abs(n);
while (m != 0) {
int temporary = m;
m = n % m;
n = temporary;
}
return n;
}
/**
* Returns the greatest common divisor (GCD) of two integer numbers.
*
* @param m first of the two integer numbers whose GCD will be returned.
* @param n second of the two integer numbers whose GCD will be returned.
* @return the greatest common divisor of m and n.
* @pre m ≠ 0 ∨ n ≠ 0
* @post gcd = gcd(m, n)
*/
public static int gcd(int m, int n)
Implementação alternativa:
funcionamento diferente.
Mesma interface: usa-se da
mesma forma, faz o mesmo.

11. 2013/2014 Fundamentos de Programação 11

12. private final double abscissa;
private final double ordinate;
{
this.abscissa = abscissa;
this.ordinate = ordinate;
}
{
return abscissa;
}
{
return ordinate;
}
{
return Math.sqrt(abscissa * abscissa + ordinate * ordinate);
}
{
return Math.atan2(ordinate, abscissa);
}
}
2013/2014 Fundamentos de Programação 12
public class Point {
public Point(final double abscissa, final double ordinate)
public double getAbscissa()
public double getOrdinate()
public double getRadius()
public double getAngle()
}
private final double abscissa;
private final double ordinate;
{
this.abscissa = abscissa;
this.ordinate = ordinate;
}
{
return abscissa;
}
{
return ordinate;
}
{
return Math.sqrt(abscissa * abscissa + ordinate * ordinate);
}
{
return Math.atan2(ordinate, abscissa);
}
}
Interface:
• Como se usa.
Interface em documentação (omissa):
• O que representa.
• Como se comporta.
• Contratos.
• Etc.
Implementação:
• Como funciona.

13. public class Point {
private double rho;
private double theta;
public Point(final double abscissa, final double ordinate) {
rho = Math.sqrt(abscissa * abscissa + ordinate * ordinate);
theta = Math.atan2(ordinate, abscissa);
}
public double getAbscissa() {
return rho * Math.cos(theta);
}
public double getOrdinate() {
return rho * Math.sin(theta);
}
public double getRadius() {
return rho;
}
public double getAngle() {
return theta;
}
}
2013/2014 Fundamentos de Programação 13
private final double rho;
private final double theta;
{
rho = Math.sqrt(abscissa * abscissa + ordinate * ordinate);
theta = Math.atan2(ordinate, abscissa);
}
{
return rho * Math.cos(theta);
}
{
return rho * Math.sin(theta);
}
{
return rho;
}
{
return theta;
}
}
public class Point {
public Point(final double abscissa, final double ordinate)
public double getAbscissa()
public double getOrdinate()
public double getRadius()
public double getAngle()
}
Implementação alternativa:
• Funcionamento diferente.
Mesma interface:
• Usa-se da mesma forma!

14.  Pode-se controlar acesso a membros de classes
 Usam-se modificadores de acesso
 public
 protected
 private
 Java tem quatro categorias de acesso
 Público – acesso sem restrição
 Protegido
 Por omissão ou privado ao pacote
 Privado – acesso apenas no contexto da própria classe
2013/2014 Fundamentos de Programação 14

15. Característica de classe Tipo Acesso
Operações Interface Público
Propriedades (operações inspectoras obtêm e
operações modificadoras alteram)
Interface Público
Métodos auxiliares Implementação Privado
Métodos enquanto implementação de operações Implementação Público
Atributos Implementação Privados
2013/2014 Fundamentos de Programação 15

16.  Propriedades são interface (inspectores e
modificadores)
public class Rational {
…
public int getNumerator() { … }
public int getDenominator() { … }
…
}
Rational rational = new Rational(1, 4);
out.println(rational.getDenominator());
2013/2014 Fundamentos de Programação 16
Por razões históricas, os inspectores
das propriedades começam com o
horrível prefixo get.

17.  Atributos são implementação
public class Rational {
private int numerator;
private int denominator;
…
}
Rational rational = new Rational(1, 4);
rational.denominator = 0;
2013/2014 Fundamentos de Programação 17

18.  Métodos auxiliares são implementação
public class Rational {
…
public Rational(final int numerator, final int denominator) {
…
reduce();
}
…
private void reduce() {
final int gcd = IntegerUtilities.gcd(numerator, denominator);
numerator /= gcd;
denominator /= gcd;
}
…
}
Rational rational = new Rational(2, 8);
rational.reduce();
2013/2014 Fundamentos de Programação 18

19.  Inicializações e atribuições
afectam apenas
referências!
 Necessário construtor por
cópia
public class Point {
…
public Point(final Point
other) {
abscissa =
other.getAbscissa();
ordinate =
other.getOrdinate();
}
…
private final double abscissa;
private final double ordinate;
}
Point a = new Point(1.0, -2.0);
Point b = a;
Point c = new Point(a);
2013/2014 Fundamentos de Programação 19
a
(1; -2)
b
c
(1; -2)

20.  Operador == com
referências verifica
identidade e não
igualdade!
 Necessária operação!
public class Point {
…
public boolean isEqualTo(
final Point other) {
return getAbscissa() ==
other.getAbscissa()
&& getOrdinate() ==
other.getOrdinate();
}
…
}
Point a = new Point(1.0, -2.0);
Point b = a;
Point c = new Point(a);
2013/2014 Fundamentos de Programação 20
a
(1; -2)
b
c
(1; -2)
b == a? Sim.
c == a? Não!
b.isEqualTo(a)? Sim.
c.isEqualTo(a)? Sim!
Mais tarde usaremos equals().

21.  Encapsulação em Java
 Abstracção
 Módulos em Java
 Interface vs. implementação
 Modificadores de acesso public e private
 Vantagens da encapsulação
 Cópia de instâncias usando construtor
 Igualdade entre instâncias usando operação
2013/2014 Fundamentos de Programação 21

22.  Encapsulamento
 Cópia de instâncias
 Igualdade entre instâncias
2013/2014 Fundamentos de Programação 22